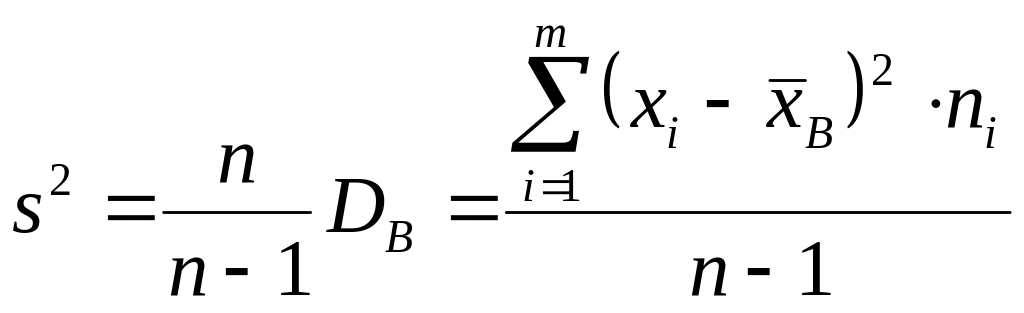20. Вариационные ряды и их характеристики.
20.1.Вариационные ряды и их графическое изображение.
Множество всех объектов, подлежащих исследованию, называют генеральной совокупностью. Множество объектов, случайным образом отобранных из генеральной совокупности, называется выборкой.
Объемом совокупности (генеральной или выборочной) называют число объектов число объектов этой совокупности.
Последовательность
результатов наблюдения
![]() ,
записанных в порядке неубывания, т.е.
,
записанных в порядке неубывания, т.е.
![]() называется вариационным рядом.
называется вариационным рядом.
Если варианты
при наблюдении встретились соответственно
![]() раз, то числа
называются частотами. Если объем выборки
равен п, то
раз, то числа
называются частотами. Если объем выборки
равен п, то
![]() .
.
Отношения частот
к объему выборки
![]() называются относительными частотами.
называются относительными частотами.
Результаты наблюдения оформляются в виде таблицы, которая называется статистическим распределением выборки.
Статистическая таблица частот |
||||
Варианты
|
|
|
|
|
Частоты
|
|
|
|
|
Статистическая таблица относительных частот |
||||
Варианты |
|
|
|
|
Относительные
частоты
|
|
|
|
|
Для большей наглядности статистические распределения изображают графически. Полученная ломанная линия называется полигоном частот.
Во многих задачах значения признака разбивают на группы. Статистическое распределение выборки задают в виде последовательности интервалов и соответствующих им частот. В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал.
Если каждое значение
частоты разделить на длину
![]() соответствующего интервала, то полученные
числа
соответствующего интервала, то полученные
числа
![]() называют плотностями частот.
называют плотностями частот.
Если каждое значение
относительной частоты разделить на
длину
соответствующего интервала, то полученные
числа
![]() называют плотностями относительных
частот.
называют плотностями относительных
частот.
Для наглядности изображения статистической таблицы строят ступенчатую фигуру, состоящую из прямоугольников, в основании которых лежат интервалы, а высотами являются соответствующими им плотности частот или относительные плотности частот.
20.2. Числовые характеристики вариационных рядов.
Средним арифметическим
называется постоянная, равная сумме
произведений значений признака на
соответствующие значения относительных
частот
 .
.
Размахом вариации
R называется разность между наибольшим
и наименьшим значениями признака
![]() .
.
Модой Мо называется значение признака, встречающееся с наибольшей частотой, т.е. наиболее типичное в данном вариационном ряду. Медианой Ме называется значение признака, лежащее в середине вариационного ряда, если этот ряд имеет нечетное число членов, и среднее арифметическое двух значений признака, расположенных в середине ряда, если ряд состоит из четного числа членов.
20.3. Статистические оценки параметров распределения.
Пусть все объекты наблюдения изучают относительно некоторого количественного признака Х. Они образуют генеральную совокупность с объемом N. Статистическая таблица частот генеральной совокупности имеет вид
|
|
|
|
|
|
|
|
Где
![]() .
.
Генеральную среднюю подсчитывают по формуле
![]() ,
,
а генеральную дисперсию по формулам:
 ,
,
 .
.
На практике обычно
из генеральной совокупности случайным
образом выбирают п объектов и изучают
полученную выборку, подсчитывая
выборочную среднюю
![]() и выборочную дисперсию
и выборочную дисперсию
![]() .
.
Выборочная средняя,
найденная по данным одной выборки,
является определенным числом. Если же
извлечь из генеральной совокупности
другие выборки, то выборочная средняя
будет меняться от совокупности к
совокупности и, следовательно, является
случайной величиной
![]() .
.
Математическое
ожидание случайной величины
равно арифметической средней генеральной
совокупности
![]() .
.
Статистическая оценка, определяемая одним числом, называется точечной. Точечная оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру при любом объеме выборки. Выборочная средняя является несмещенной оценкой генеральной средней.
Выборочная дисперсия является заниженной оценкой генеральной дисперсии. Несмещенной оценкой генеральной дисперсии является исправленная дисперсия.