17.5. Непрерывные случайные величины.

Случайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Функция распределения непрерывной случайной величины.

Функцией распределения случайной величины X называется функция , выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х.

.

Свойства функции распределения:

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей .

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. если , то .

3. , .

4. Вероятность попадания случайной величины Х в интервал равна приращению ее функции распределения на этом интервале: .

Плотность вероятности.

Плотностью вероятности непрерывной случайной величины Х называется производная ее функции распределения.

.

График плотности вероятности называется кривой распределения.

Свойства плотности вероятности:

1. Плотность вероятности – неотрицательная функция .

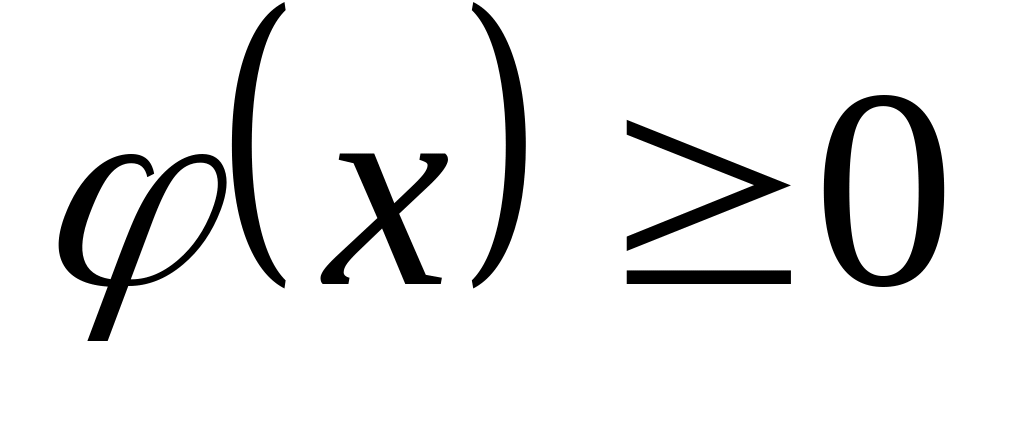2. Вероятность попадания непрерывной случайной величины в интервал 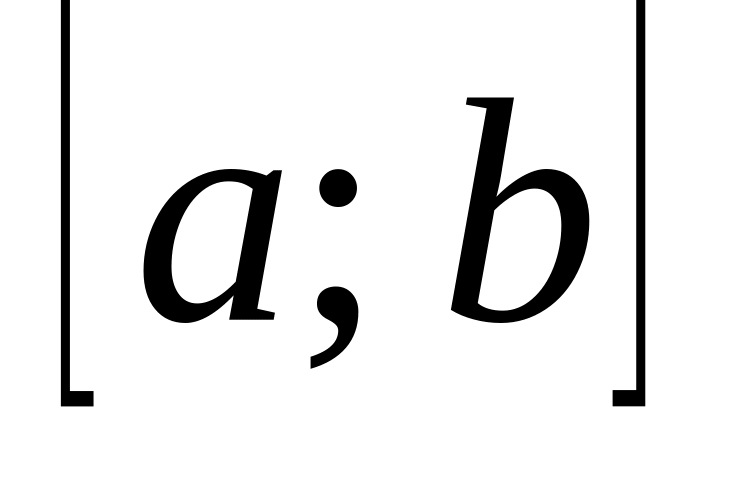равна определенному интегралу от ее плотности вероятности в пределах от а до b .

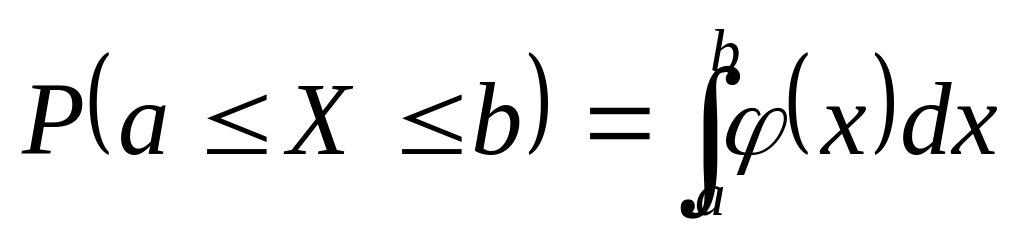3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле

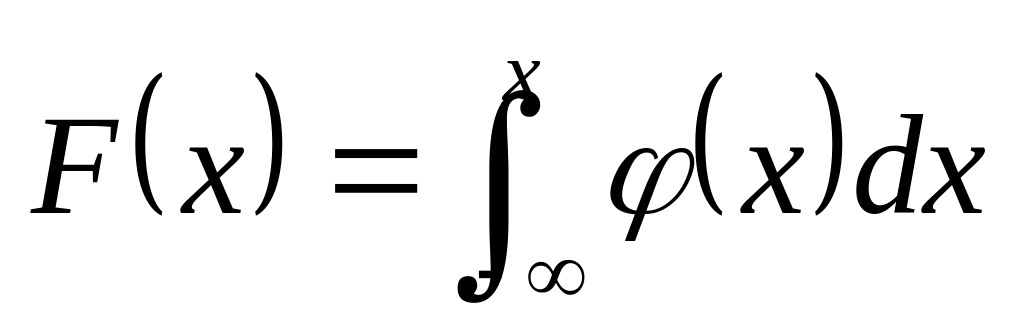
4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: .

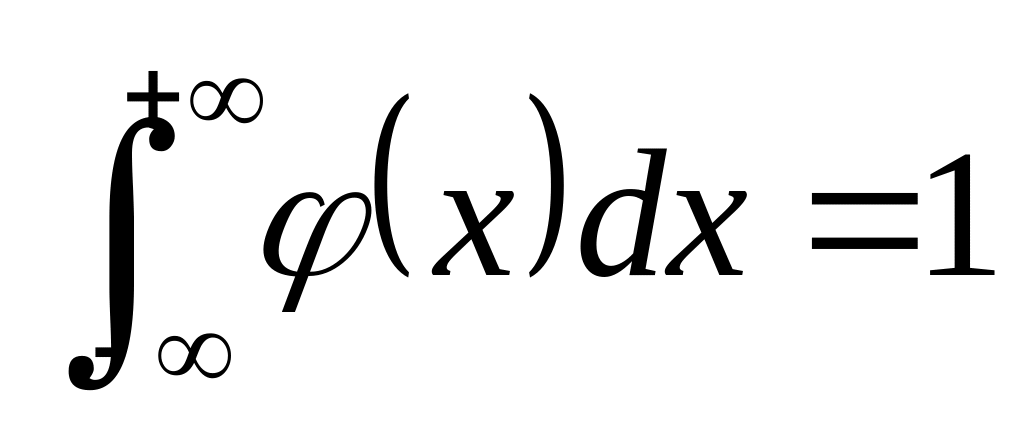Геометрически свойства плотности вероятности означают, что ее график лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Для непрерывной случайной величины Х:

, если интеграл абсолютно сходятся;

или , если приведенные интегралы сходятся.

Пример 3. Функция распределения случайной величины Х определяется выражением

Найти: а) плотность распределения вероятностей, б) вероятность попадания величины Х на участок от 0,25 до 0,5.

а)

б)

Пример 4. Непрерывная случайная величина Х подчинена закону распределения с плотностью

Найти: а) функцию распределения , б) вероятность попадания случайной величины Х на участок от 0 до

Если , то

Если , то

Если , то

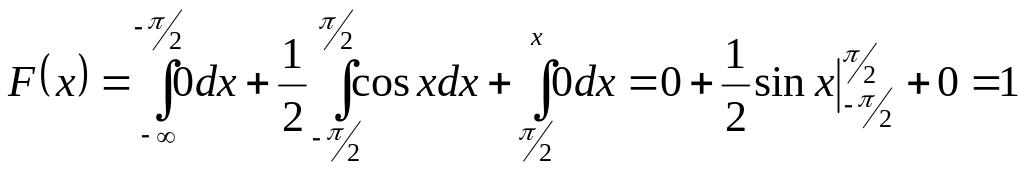
17.6. Мода и медиана. Квантили. Моменты случайных величин.

Модой случайной величины Х называется ее наиболее вероятное значение (для которого вероятность или плотность вероятности достигает максимума).

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.

Медианой непрерывной случайной величины Х называется такое ее значение, для которого , т.е. вероятность того, что случайная величина примет значение, меньшее медианы или большее ее, одна и та же и равна .

Геометрически вертикальная прямая, проходящая через точку с абсциссой, равной , делит площадь фигуры под кривой распределения на две равные части.

Квантилем уровня q называется такое значение случайной величины, при котором функция ее распределения принимает значение, равное q, т.е. .

Медиана случайной величины есть квантиль уровня 0,5. Квантили и называются верхним и нижним квантилем. Квантиль называется процентной точкой. .