17.2. Математическое ожидание дискретной случайной величины.

Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности:

.

Свойства математического ожидания.

1. Математическое ожидание постоянной величины равно самой постоянной: .

2. Постоянный множитель можно выносить за знак математического ожидания .

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий .

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий .

5. Если все значения случайной величины увеличить на постоянную С, то на эту же постоянную увеличится математическое ожидание этой случайной величины. .

6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю .

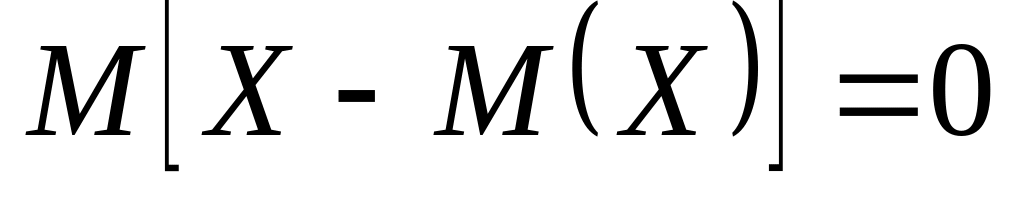Найдем математическое ожидание в примере 1

Пример 2. Известны законы распределения случайных величин X и Y – числа очков, выбиваемых первым и вторым стрелками.

xi	0	1	2	3	4	5	6	7	8	9	10
pi	0,15	0,11	0,04	0,05	0,04	0,10	0,10	0,04	0,05	0,12	0,20

yi	0	1	2	3	4	5	6	7	8	9	10
pi	0,01	0,03	0,05	0,09	0,11	0,24	0,21	0,10	0,10	0,04	0,02

Необходимо выяснить, какой из двух стрелков стреляет лучше.

Очевидно, что из двух стрелков лучше стреляет тот, кто в среднем выбивает большее количество очков

17.3. Дисперсия дискретной случайной величины.

Дисперсией случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:

.

Если случайная величина Х – дискретная с конечным числом значений, то , где

Если случайная величина Х – дискретная с бесконечным счетным множеством значений, то .

Средним квадратичным отклонением (стандартным отклонением или стандартом) называется .

Свойства дисперсии случайной величины.

1. Дисперсия постоянной величины равна нулю: .

2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат .

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

4. Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий .

Пример 1.

Пример 2. Известны законы распределения случайных величин X и Y – числа очков, выбиваемых первым и вторым стрелками.

xi	0	1	2	3	4	5	6	7	8	9	10
pi	0,15	0,11	0,04	0,05	0,04	0,10	0,10	0,04	0,05	0,12	0,20

yi	0	1	2	3	4	5	6	7	8	9	10
pi	0,01	0,03	0,05	0,09	0,11	0,24	0,21	0,10	0,10	0,04	0,02

Необходимо выяснить, какой из двух стрелков стреляет лучше.

Вычислить дисперсию и среднее квадратическое отклонение.