Расчет цилиндрической косозубой и шевронной передач на контактную прочность

Расчет на контактную прочность косозубых и шевронных колес производят аналогично расчету прямозубых колес, он является основным. Рас­положение зубьев в косозубом зацеплении повышает коэффициент пере­крытия зубьев, так как в зацеплении находится одновременно несколько пар зубьев, что уменьшает нагрузку на один зуб и повышает его контакт­ную прочность, увеличивает прочность зубьев на изгиб, уменьшает дина­мические нагрузки. Для учета повышения контактной прочности косых зубьев по сравнению с прямыми в формулу (21) вводят поправочные коэффициенты.

Контактные напряжения, возникающие в поверхностном слое косых зубьев:

                                    (25)

где   — коэффициент, учитывающий форму сопряжения по­верхностей зубьев (среднее значение  );  =275 МПа — коэффи­циент, учитывающий механические свойства материала сопряженных ко­лес;   — коэффициент, учитывающий суммарную длину кон­тактных линий (для косозубых передач среднее значение  );   — коэффициент, учитывающий распределение нагрузки между зубьями (вы­бирается по табл. 16);   (табл. 6),   (табл.7) — коэффициенты ре­жима работы;   — коэффициент длины зуба ( — табл. 9);   — межосевое расстояние, мм;   — передаточное отноше­ние;   —момент на колесе, Нмм;   — допускаемое контактное напря­жение, МПа.

 

Проектировочный расчет на контактную прочность.

Аналогично расчету прямозубой передачи получим фор­мулу проектировочного расчета для определения межосевого расстояния косозубой передачи:

                                                                                  (26)

где   — вспомогательный коэффициент ( = 43 МПа^1/3 с учетом  ).

 

Допускаемые нормальные контактные напряжения для расчета ци­линдрической косозубой передачи определяют как и для рассмотренных прямозубых передач. Часто материалы для шестерни и коле­са выбирают одинаковыми. Разные допускаемые контактные напряжения для шестерни и колеса обеспечиваются путем их различной термической обработки. Предпочтительные марки сталей даны в табл. 13.

В качестве допускаемого контактного напряжения (расчетного) для косозубых и шевронных цилиндрических передач принимают значение немного  меньше  среднего  арифметического  между  значениями   и  , т.е.

                                                                                   (27)

где  — допускаемое (расчетное) контактное напряжение;   — допус­каемое контактное напряжение для материала шестерни;   — допускае­мое контактное напряжение для материала колеса.

Расчетное   не может быть принято большим, чем  .

 

Последовательность проектировочного расчета цилиндрической косозубой передачи

Последовательность приведенного расчета аналогична расчету цилинд­рической прямозубой передачи.

Последовательность расчета закрытой цилиндрической косозубой передачи.

1.  Определить передаточное число  .

2. В зависимости от условий работы передачи выбрать материалы ко­лес, назначить термическую обработку и твердость рабочих поверхностей зубьев.

3. Определить базовое число циклов  ,  расчетную циклическую долговечность, определить допускаемые напряжения изгиба и контактные напряжения.

4.  Выбрать коэффициент   длины зуба (ширины венца колеса).

5. Определить межосевое расстояние из условия контактной прочности по формуле (26).

6.  Задать    значение    нормального    модуля    из    соотношения   и округлить его до ближайшего стандартного значения (см. табл. 3). При этом для силовых передач желательно иметь модуль не ме­нее 1,5—2 мм.

7.  Задать угол наклона зубьев   и определить суммарное число зубьев  , передачи, числа зубьев шестерни и колеса   и  .

8. Определить эквивалентные числа зубьев   и   и коэффициенты фор­мы зуба   и  .

9.  По формуле (23) проверить прочность зубьев по напряжениям из­гиба. При неудовлетворительных результатах (  или  ) необ­ходимо путем соответствующего изменения числа зубьев и модуля при том же межосевом расстоянии добиться определенного изменения напряжения изгиба, не нарушая условия контактной прочности.

10.  Произвести геометрический расчет передачи (см. табл. 15). Опре­делить окружную скорость колес и по табл. 14 назначить соответствую­щую степень точности, выбрать   (табл. 16).

Расчет открытых передач (часто открытые передачи рассчитыва­ют так же, как закрытые).

1.  Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы для колес, назначить их термическую обработку и твердость рабочих поверхно­стей зубьев.

3.  Определить базу испытаний базового числа циклов  , расчетную циклическую нагрузку, вычислить коэффициенты и определить допускае­мые напряжения изгиба.

4.  Задать угол наклона зубьев   и число зубьев шестерни 

5. Определить число зубьев колеса 

6. Определить числа зубьев эквивалентных колес, шестерни и колеса   и   по табл.6 коэффициенты формы зуба   и  .

7.  Выбрать  — коэффициент длины зуба (ширины венца).

8.  Из условия прочности на изгиб определить по формуле (24) значе­ние нормального модуля   и округлить до ближайшего большего стан­дартного значения (см. табл. 3).

9.  Произвести геометрический расчет передачи (см. табл. 15).   

10.  Определить окружную скорость колес   и по табл. 14 назначить соответствующую ей степень точности.

 

Конические зубчатые передачи. Устройство и основные геометрические и силовые соотношения

Зубчатую передачу с пересекающимися осями, у которой начальные и делительные поверхности колес конические, называют конической.

Коническая передача состоит из двух конических зубчатых колес (рис. 45) и служит для передачи вращающего момента между валами с пересекающимися осями под углом  . Наиболее распространена вмашиностроении коническая передача с углом между осями Z=90⁰ (рис. 47), но могут быть передачи и с  . Колеса конических передач. выполняют с прямыми (рис. 46, а), косыми (рис. 46, б), круговыми зубьями (рис. 46, в).

 

Рис. 45.  Коническая  пря­мозубая передача

 

Рис. 46. Конические зубчатые колеса: а — коле­со с прямыми зубьями;

б — колесо с косыми зу­бьями; в — колесо с круговыми зубьями

 

Рис. 47. Геометрические параметры конических зубчатых колес

 

Рис. 48. Гипоиднаяя передача

 

Передачу с коническими колесами для передачи вращающего момента между валами со скрещиваю­щимися осями называют гипоидной (рис. 48). Эта передача находит применение в автомобилях.

По стоимости конические передачи дороже ци­линдрических при равных силовых параметрах. Их применение диктуется только необходимостью пе­редавать момент при пересекающихся осях валов. Передаточное число одной пары  .

 

Вершины начальных и делительных конусов конической передачи на­ходятся в точке пересечения осей валов О (рис. 50). Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрическиепараметры конической передачи (рис. 47 и 50):

АОВ — делительный конус шестерни;

ВОС — делительный конус колеса;

АО₁В — делительный дополнительный конус шестерни;

ВО₂С — делительный дополнительный конус колеса;

 — угол делительного конуса шестерни;

 — угол делительного конуса колеса;

d_e[ — внешний делительный диаметр шестерни;

d_e2 — то же, колеса;

d₁ — средний делительный диаметр шестерни;

d₂ — то же, колеса;

b — ширина зубчатого венца (длина зуба);

R_e — внешнее делительное конусное расстояние (или длина дис­танции).

Рис. 50. Коническая прямозубая передача

 

Передаточное число конической передачи определяется так:

В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают внешнюю и среднюю делительные окружности (см. рис. 47).

Из условия, что в конической передаче модуль и делительный связаны теми же соотношениями, что и в цилиндрических передачах, т.е. d=mz (рис.51), определяют внешний d_e и средний d_m делительные метры:

где т_е — внешний окружной модуль; т_т — средний окружной модуль.

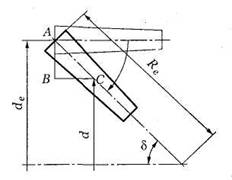
Рис. 51. Зуб конического колеса

 

Внешний окружной модуль обычно выбирают из стандартного ряда (см. табл. 3). Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все геометрические параметры зубча­тых колес (задают размеры зубьев на внешнем торце, на котором удобно производить измерения).

Средний окружной модуль т рассчитывают в зависимости от внешнего окружного модуля т_е. По среднему окружному модулю производят расчет передачи на прочность при изгибе.

Рис. 52

 

Зависимость между т_е и т_т в конической передаче.

Из рис. 3.51  , где   (из  ). Отсюда  .

Умножив левую и правую части равенства на два, получим  . Разделив левую и правую части равенства на  , получим

 или 

Геометрические соотношения размеров прямозубой конической пере­дачи с эвольвентным профилем зуба. Согласно рис. 53 внешний диаметр вершин зубьев

внешний диаметр впадин зубьев

Длина зуба (ширина венца)   [  при условии   и  , где   — средний делительный диаметр шес­терни].

Рис. 53. Геометрия прямозубой конической передачи

 

Ориентировочно длина зуба может быть выбрана также в зависимости от внешнего делительного конусного расстояния R_e:

.

 

Таблица 17. Геометрические параметры прямозубой конической передачи

Параметр, обозначение	Расчетные формулы
Внешний окружной модуль
Средний окружной модуль
Внешний диаметр вершин зубьев
Внешний делительный диаметр
Внешний диаметр впадин зубьев
Высота зуба
Высота головки зуба
Высота ножки зуба
Окружной шаг
Окружная толщина зуба
Окружная ширина впадины
Радиальный зазор
Ширина зубчатого венца
Внешнее делительное конусное расстояние
Угол делительного конуса шестерни
колеса

 

Силы в зацеплении прямозубой конической передачи. В рассматривае­мой передаче действует одна сила, обусловленная давлением зуба шестерни на зуб колеса. Эта сила для удобства расчетов раскладывается на 3 состав­ляющие: окружная F_t, радиальная F_r и осевая F_a.

С учетом геометрических соотношений в конической передаче по нор­мали к зубу действует сила F_n1 (рис. 54). Эту силу разложим на две состав­ляющие:   и  . В свою очередь   разложим на   и  . Запишем:

;   ;   .

Осевая сила на шестерне численно равна радиальной силе на колесе.

Рис. 54. Силы в зацеплении прямозубой конической передачи

Рис.55

 

Рис. 56

 

Расчет зубьев прямозубой конической передачи на изгиб

Расчет производят по аналогии с расчетом цилиндрической прямозу­бой передачи.

Опытным путем установлено, что нагрузочная способность конической передачи ниже, чем цилиндрической. В соответствии с этим в расчетные фор­мулы для зубьев конической передачи вводят коэффициент К_FO, учитываю­щий снижение их нагрузочной способности по сравнению с зубьями ци­линдрических передач.

Расчет на прочность зубьев при изгибе производят по среднему значе­нию модуля зубьев т. Коэффициент формы зуба Y_F выбирают по аналогии с цилиндрической прямозубой передачей, но в зависимости от числа зубь­ев эквивалентных колес  .

Под числом зубьев   эквивалентных колес понимают такое число зубь­ев, которое может расположиться на длине окружности (см. рис. 47) ра­диусом, равным длине образующей дополнительного конуса О₁А.

 

Проверочный расчет следует проводить по аналогии с прямозубой пе­редачей.

Расчетные напряжения изгиба в зубьях конических колес и условие прочности выражаются формулой

                                                 (28)

где   — возникающее напряжение изгиба, МПа;   — вращающий момент на колесе, Нмм;  ,   — коэффициенты нагрузки (см. табл. 6, 7);   — коэффициент длины зуба;   — коэффициент формы зуба (выбирают по табл. 8) в зависимости от  ;   — число зубьев шестер­ни; и — передаточное число;   — средний модуль, мм;   = 0,85 — опытный коэффициент снижения нагрузочной способности;   —допускаемое напряжение изгиба, МПа.

Проектировочный расчет. Средний модуль зубьев определяется по формуле

                                                              (29)

где т, мм; Т₂, Нмм;  , МПа; К_т= 1,45 — вспомогательный коэффици­ент для стальных прямозубых конических колес;   принимают  .