§ 6.Производные высших порядков

Определение 1. Пусть функция имеет производную в , т.е. . Если , то она называется производной II порядка функции в точке и обозначается .

Итак, .

Аналогично: .

Производная -го порядка функции в точке определяется индуктивно, т.е. , .

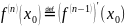Определение 2. Функция называется дважды дифференцируемой в точке , если .

Определение 3. Производной II порядка функции называется функция , где , причем .

Техника вычисления производных высших порядков заключается в последовательном вычислении производных от I-го до указанного порядка.

Примеры.

1) . .

2) . .

3) . .

4) . .

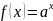5) .

,

,

.

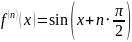6) Свободное падение тела происходит по закону , – ускорение свободного падения.

– скорость в момент времени .

– ускорение свободного падения (в этом заключается механический смысл II производной).

7) Прямолинейное движение описывается функцией

откуда

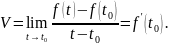
Если дифференцируема в самой точке и в некоторой ее окрестности , то определена в . пусть дифференцируема в точке . Тогда по определению: – это есть ускорение в момент времени .

Упражнение.

Доказать: .

§ 7. Формула Тейлора для многочленов

Рассмотрим многочлен -й степени:

, где .

Известно, что многочлены одной и той же степени отличаются коэффициентами при одинаковых степенях . А есть ли связь между коэффициентами многочлена и самим многочленом?

Теорема. Любой многочлен определяется своим значением и значениями своих производных в точке , а именно:

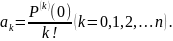
Доказательство.

Вычислим :

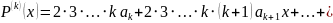
Вычислим значения в точке : . Откуда: .

Итак, имеем: – формула Тейлора для многочлена .

Пример.

,

,

,

…

,

.

Т.о., .

Следствие 1 (бином Ньютона).

Следствие 2. Формула Тейлора в точке имеет вид:

Доказательство.

Обозначим .Тогда и . По формуле Тейлора: .

Следствие 3. Пусть – произвольные действительные числа и . Тогда существует единственный многочлен степени , для которого .

Очевидно, .

Упражнения.

1) Разложить по степеням многочлен .

2) Разложить по степеням многочлен .

3) Найти все многочлены III степени, у которых .