
ОДЕСЬКИЙ НАЦІОНАЛЬНИЙ МОРСЬКИЙ УНІВЕРСИТЕТ
Кафедра „Економічна теорія та кібернетика”
МЕТОДИЧНІ ВКАЗІВКИ
до практичних занять
з дисципліни „ЕКОНОМЕТРІЯ”
ОДЕСА - 2009
Методичні вказівки опрацьовано к.е.н. Москалюк Ларисою Володимирівною- доцентом кафедри «Економічна теорія та кібернетика» Одеського національного морського університету та Давидовою Валентиною Іванівною – асистентом тієї ж кафедри.
Методичні вказівки схвалено кафедрою «Економічна теорія та кібернетика» ОНМУ протокол № 13 від 30.06.2009
Рецензент к.е.н. Холоденко А.М.
Практичне заняття №1
Знаходження
рівняння простої лінійної регресії й
оцінка моделей через середню помилку
апроксимації
![]() та
та
![]() - критерій (Фішера).
- критерій (Фішера).
Вхідні дані:
№ |
y |
x |
|
|
|
Порядок виконання завдання:
Для характеристики залежності
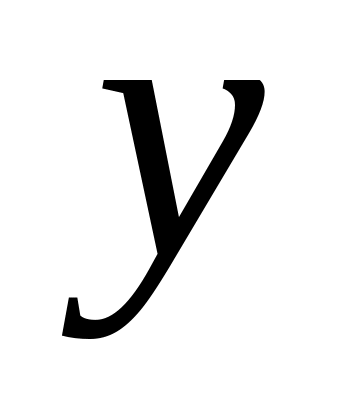 від
від
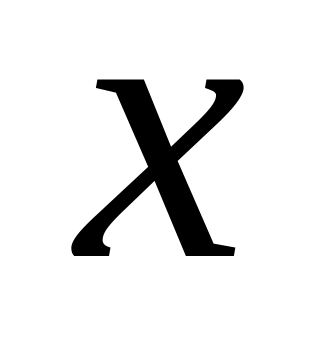 знайти параметри
знайти параметри
 і
і
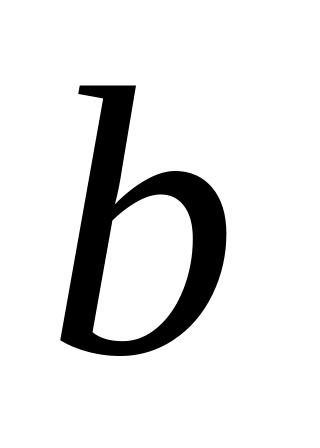 функції
функції
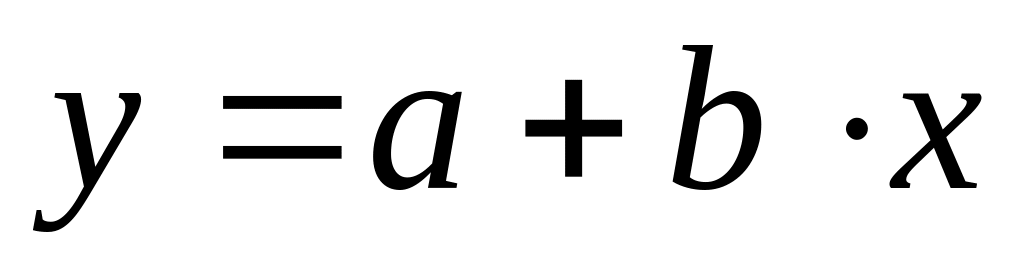 методом
найменших квадратів (МНК).
методом
найменших квадратів (МНК).Знайти коефіцієнт парної кореляції rху.
Визначити коефіцієнт детермінації R2 і дати економічну інтерпретацію отриманих результатів.
Знайти величину середньої помилки апроксимації .
Розрахувати значення F – критерію.
Зробити висновки про справедливість гіпотези Н0 (Про випадкову природу виявленої залежності, про статистичну значимість параметрів рівняння та показник щільності зв'язку).
Проста або парна регресія – це регресія між двома змінними та . Рівняння простої регресії характеризує зв'язок між цими змінними, яка з'являється як деяка закономірність тільки в середньому по сукупності спостережень.
Рівняння регресії у загальному виді:
![]() (1)
(1)
де х – незалежна змінна або ознака – фактор;
– залежна змінна або результативна ознака.
Якщо
![]() - фактичне значення з набору вихідних
даних,
- фактичне значення з набору вихідних
даних,
![]() - теоретичне (або розрахункове) значення
залежної змінної, знайдене по формулі
(1), то
- теоретичне (або розрахункове) значення
залежної змінної, знайдене по формулі
(1), то
![]() ,
(2)
,
(2)
де
![]() - випадкова величина, що характеризує
величину відхилення фактичного значення
у
від теоретичного.
- випадкова величина, що характеризує
величину відхилення фактичного значення
у
від теоретичного.
Найпростіший вид регресії – лінійна.
Рівняння регресії в цьому випадку має вигляд:
![]() (3)
(3)
або
![]() (3’)
(3’)
Величини a, b називаються параметрами регресії , для їхнього визначення застосовують метод найменших квадратів (МНК).
Оцінки параметрів a, b знаходять із умови мінімальності суми квадратів відхилень фактичних значень у від теоретичних, тобто:
![]()
![]() ,
(4)
,
(4)
Тоді має місце система:
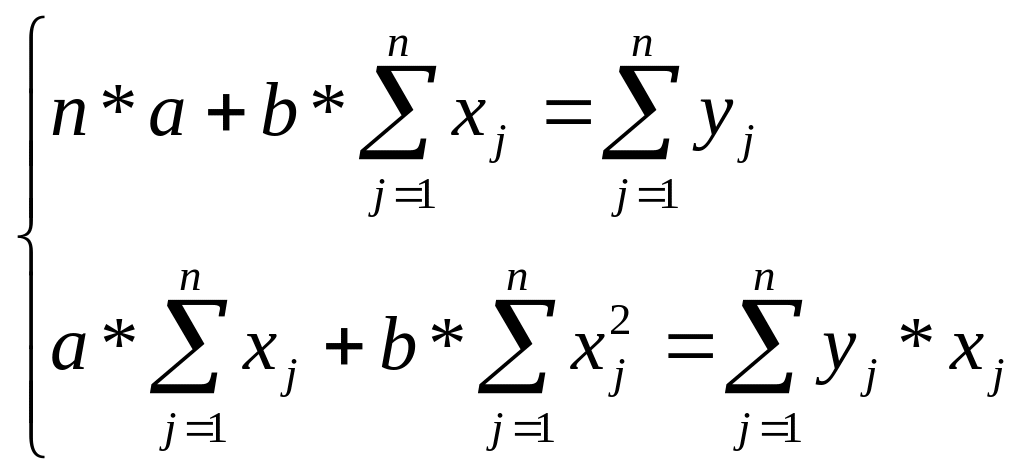 (5)
(5)
Звідси:
![]() ,
(6)
,
(6)
де
![]() - середнє квадратичне відхилення х;
- середнє квадратичне відхилення х;
![]() - середні
величини змінних
- середні
величини змінних
![]() і
і
![]() відповідно.
відповідно.
Щоб оцінити щільність зв'язку між змінними и х у випадку лінійної регресії використовують лінійний коефіцієнт кореляції rху
![]() ,
(8)
,
(8)
де
![]() -
середнє квадратичне відхилення.
-
середнє квадратичне відхилення.
Після знаходження регресії варто оцінити якість побудованої моделі, значимість рівняння і його параметрів.
Якість побудованої лінійної моделі оцінюють за допомогою коефіцієнта детермінації R2 і середньої помилки апроксимації.
![]() або
або
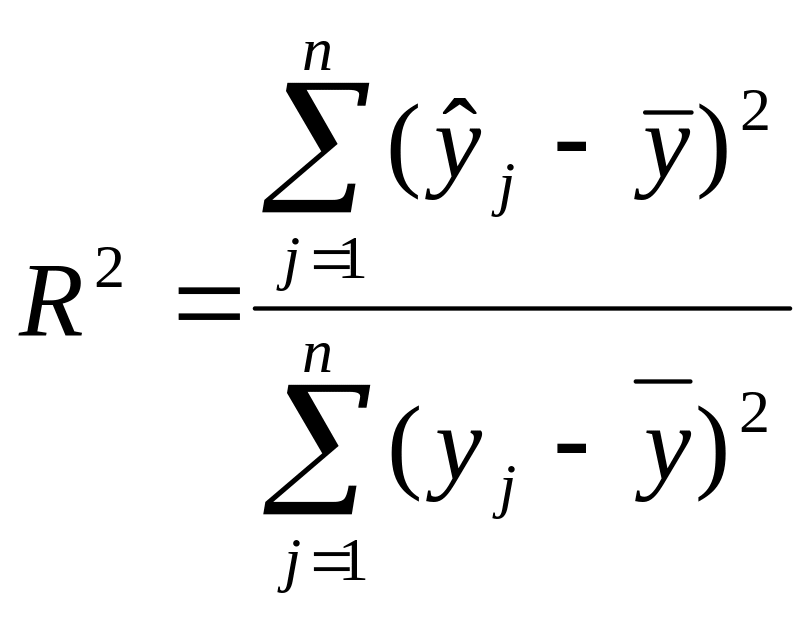 (9)
(9)
![]() (10)
(10)
Якість
рівняння регресії оцінюють за допомогою
F – критерія Фішера, який застосовується
для перевірки гіпотези
![]() про статистичну незначимість рівняння
регресії й показника щільності зв'язку.
Перевірка складається в порівнянні
значимості F – критерію Фішера фактичного
– Fфакт
(або розрахункового – Fрозр)
і критичного - Fкрит
(або табличного – Fтабл.)..
про статистичну незначимість рівняння
регресії й показника щільності зв'язку.
Перевірка складається в порівнянні
значимості F – критерію Фішера фактичного
– Fфакт
(або розрахункового – Fрозр)
і критичного - Fкрит
(або табличного – Fтабл.)..
Для лінійної моделі:
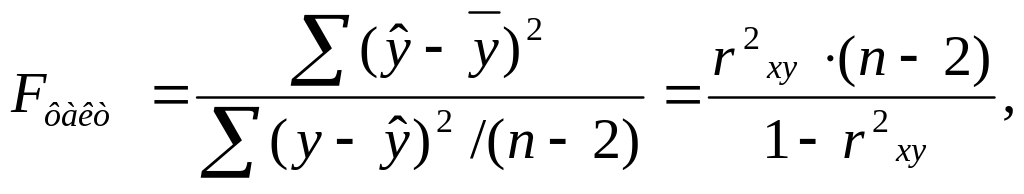 (11)
(11)
де n – число одиниць сукупності.
Рівень
значимості
![]() частіше дорівнює 0,05 або 0,01 ( рівень
значимості
- імовірність відкинути правильну
гіпотезу за умови, що вона вірна).
частіше дорівнює 0,05 або 0,01 ( рівень
значимості
- імовірність відкинути правильну
гіпотезу за умови, що вона вірна).
Якщо Fтабл < Fфакт , то Н0 відхиляється, якщо Fтабл > Fфакт , тобто гіпотеза Н0 не відхиляється, рівняння вважається статистично незначущим, ненадійним.
Статистична значимість коефіцієнтів регресії та лінійного коефіцієнта кореляції оцінюється за допомогою t – критерію Стьюдента. У цьому випадку висувається гіпотеза Н0 про випадкову або незначиму їхню відмінність від нуля. Перевірка складається в порівнянні значень t – статистик фактичних або розрахункових – tфакт або tрозр з табличними або критичними значеннями – tтабл або tкритич.
Розрахунок фактичних значень t – критерію для величини a, b, rxy виконується за формулами:
![]() (12)
(12)
де mb, ma, mr - випадкові помилки b, a і rxy відповідно.
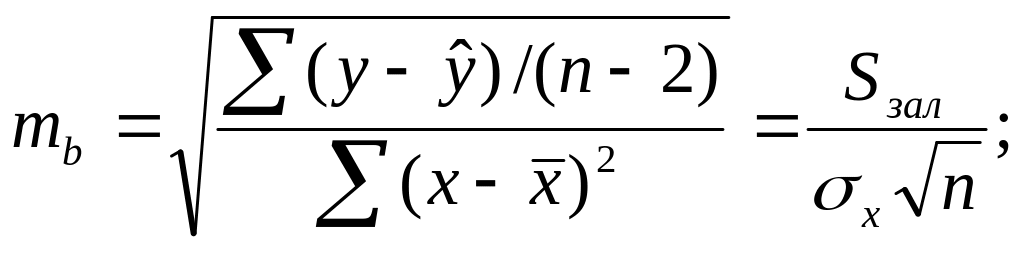
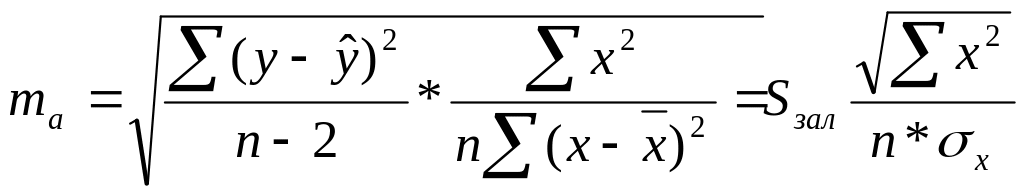
![]() (13)
(13)
Якщо tтабл < tфакт, то Н0 відхиляється, параметри a, b і rxy вважаються статистично значимими. Якщо tтабл < tфакт, то гіпотеза Н0 не відхиляється.
Для
коефіцієнтів
![]() розраховуються також довірчі інтервали.
розраховуються також довірчі інтервали.
Для параметра довірчий інтервал має вигляд:
![]() (14)
(14)
де
![]() ,
,
для параметра довірчий інтервал такий:
![]() (15)
(15)
де
![]()
Рівняння
регресії застосовується для одержання
прогнозованих значень
![]() ,
що обчислюють для відповідних прогнозованих
значень х
,
а також довірчих інтервалів для
прогнозованих значень
.
,
що обчислюють для відповідних прогнозованих
значень х
,
а також довірчих інтервалів для
прогнозованих значень
.
При цьому застосовуються відповідні формули:
![]() (16)
(16)
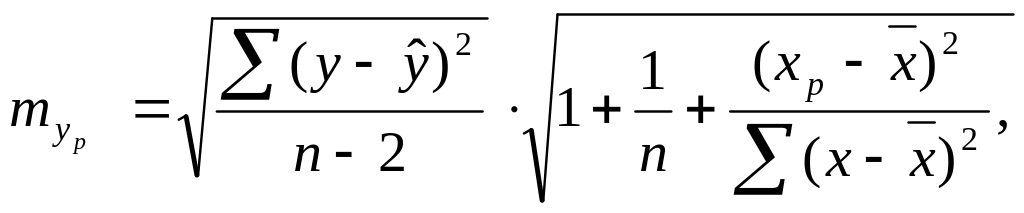 (17)
(17)
де
![]() - прогнозовані значення змінних y
і x
відповідно,
- прогнозовані значення змінних y
і x
відповідно,
![]() -
стандартна помилка прогнозу.
-
стандартна помилка прогнозу.
Довірчий
інтервал для прогнозованого значення
![]() :
:
![]() (18)
(18)
де
![]() гранична помилка для
,
гранична помилка для
,
![]()
Література: [1.С.44-102]
