6.1. Кинематический анализ мальтийского механизма

Перед разработкой конструкции мальтийского механизма следует определить основные параметры и выполнить его кинематический анализ. Исходными данными являются параметры , , . Необходимо определить:

• угол поворота креста за один оборот кривошипного вала,

• угол рабочего поворота кривошипа,

• геометрические размеры мальтийского механизма,

• угловую скорость и угловое ускорение креста.

6.1.1. Определение основных параметров

Угол поворота креста за один оборот кривошипного вала вычисляется по формуле (см. рис.6), град,

.

Угол рабочего поворота кривошипа, при котором происходит поворот креста, равен, град,

.

Угол выемки фиксирующего диска, град.,

.

Длина кривошипа, мм,

.

Расстояние от оси вращения креста до начала паза, мм,

.

Диаметр цевки кривошипа, мм,

.

Диаметр креста, мм,

,

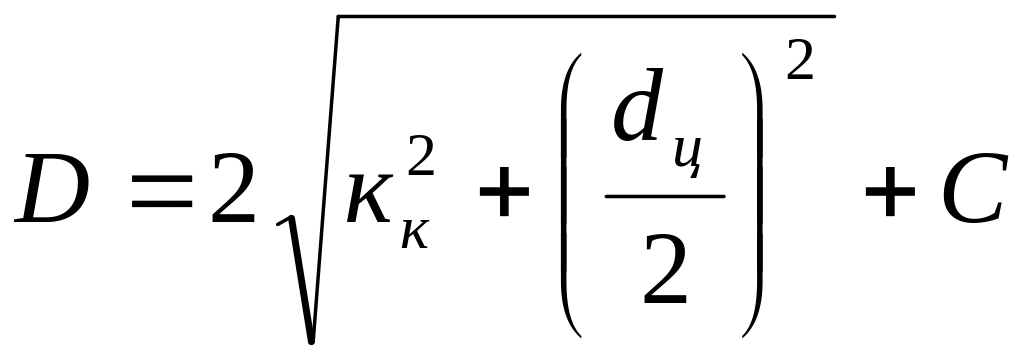где С – фаска, равная 1,5. . .2 мм.

Длина паза креста, мм,

.

Диаметры валов кривошипа и креста принимают конструктивно, соблюдая условия, мм,

, .

При разработке конструкции в дальнейшем и проверяют расчетами на прочность.

Отношение длины кривошипа к межосевому расстоянию равно

.

Диаметр скользящей поверхности диска кривошипа, мм,

.

6.1.2. Определение угловой скорости и углового ускорения креста

Угловая скорость креста мальтийского механизма зависит от угла рабочего поворота кривошипного вала и определяется по формуле, 1/c,

. (1)

Угловое ускорение определяется по формуле, 1/с ,

. (2)

Расчеты по формулам (1) и (2) необходимо выполнить при значении , изменяющемся через от

,

соответствующем входу цевки кривошипа в паз креста, до

,

соответствующем выходу цевки из паза.

Нулевое значение угла соответствует положению кривошипа, когда он совмещается с линией, соединяющей оси валов 4 и 5 (см. рис.5).

Результаты расчетов рекомендуется свести в таблицы. По этим данным построить диаграммы и .

Указания по расчету основных параметров мальтийского механизма, определению угловой скорости и ускорения креста приведены в [1], с.438. . .442; [3], с.293. . .297; [4], с.172. . .174.

6.1.3. Построение планов скоростей и ускорений звеньев

мальтийского механизма

Перед построением планов скоростей и ускорений необходимо изобразить мальтийский механизм в выбранном масштабе.

Построение следует выполнить для трех положений мальтийского механизма:

а) для момента входа цевки кривошипа в паз креста, т.е. при ;

б) для момента поворота кривошипа на ¼ рабочего угла, т.е. при ;

в) для момента поворота кривошипа на ½ рабочего угла, т.е. когда ось кривошипа совмещается с линией, соединяющей оси валов 4 и 5.

При построении планов скоростей и ускорений считаются заданными угловая скорость , угол рабочего поворота вала кривошипа , число пазов креста , межосевое расстояние и длина кривошипа .

Используя результаты построения планов необходимо определить угловые скорости и угловые ускорения вала креста для указанных выше трех положений.

В качестве примера рассмотрим построения планов скоростей и ускорений для положения кривошипа, изображенного на рис.7,а.

Будем рассматривать точку В как точку, принадлежащую одновременно кривошипу и кресту. Движение точки В, принадлежащей кривошипу, считаем абсолютным. Точка В, принадлежащая кресту находится в сложном движении – в переносном вращательном с крестом и относительном прямолинейном вдоль паза креста.

Построение планов скоростей ведем по следующему векторному уравнению:

,

где – вектор абсолютной скорости точки В, равный по модулю и направленный перпендикулярно АВ; – вектор переносной скорости точки В, равный по модулю и направленный перпендикулярно ВС; – вектор относительной скорости точки В, направленный параллельно ВС.

Выполним построение плана скоростей при положении кривошипа, когда он повернулся на ¼ рабочего угла. От полюса (рис.7,б) отклады-

а)

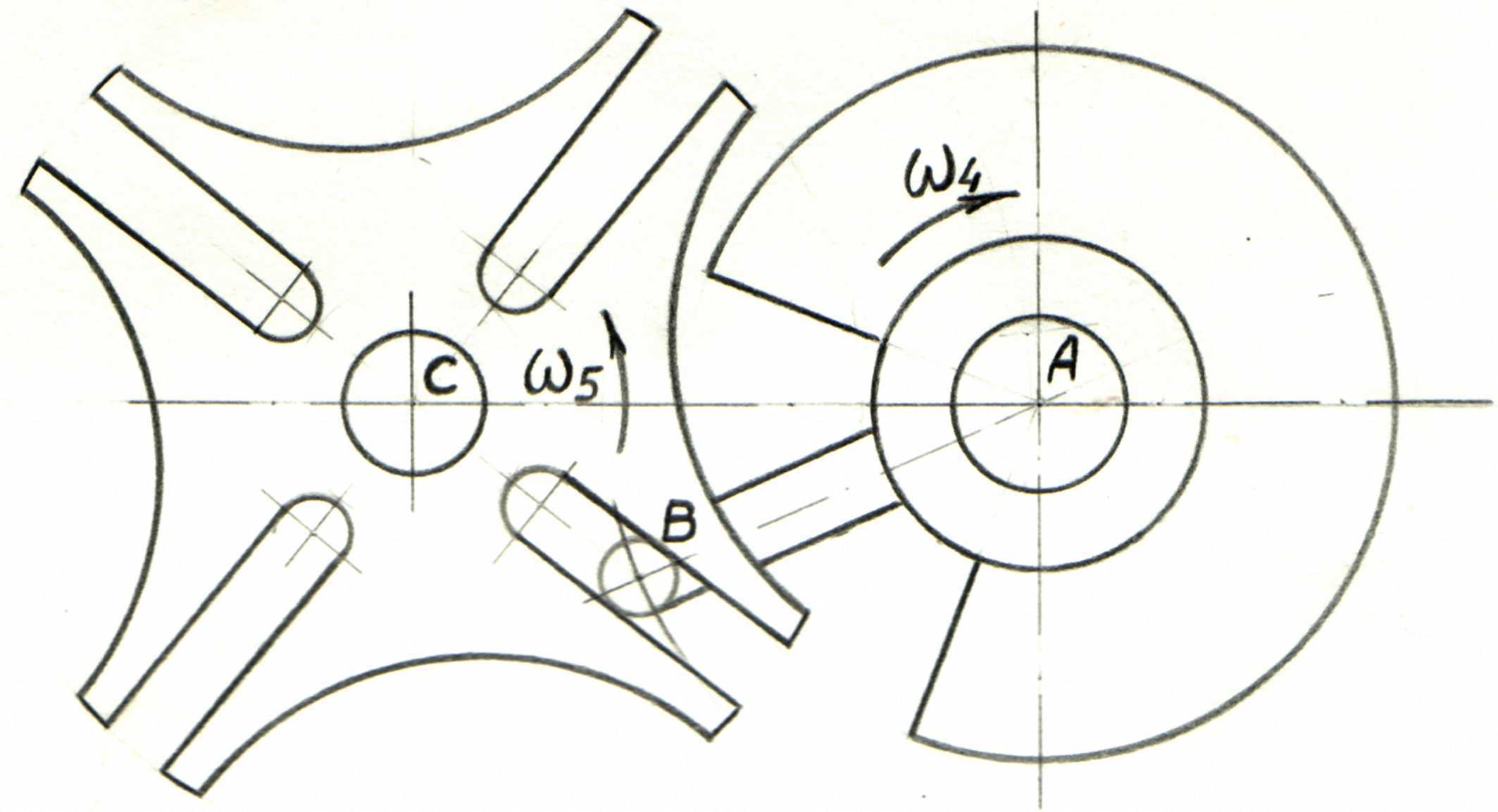
б) в)

Рис.7

ваем от резок , изображающий в определенном масштабе вектор скорости . При этом , причем если изменяется в м/c, то масштабный коэффициент – в . ( показывает, сколько единиц скорости приходится на 1 мм отрезка ). Затем из точки проведем прямую перпендикулярно ВС, а через точку b – прямую параллельно ВС. Точка их пересечения k является концом вектора и началом вектора . Определим модуль вектора из плана с учетом масштабного коэффициента , т.е. (м/c). Так как скорость зависит от угловой скорости креста, то величина угловой скорости (1/c). Здесь – расстояние от точки В до центра вращения креста в м.

При построении плана скоростей для первого положения мальтийского механизма следует иметь в виду, что , а для третьего положения – .

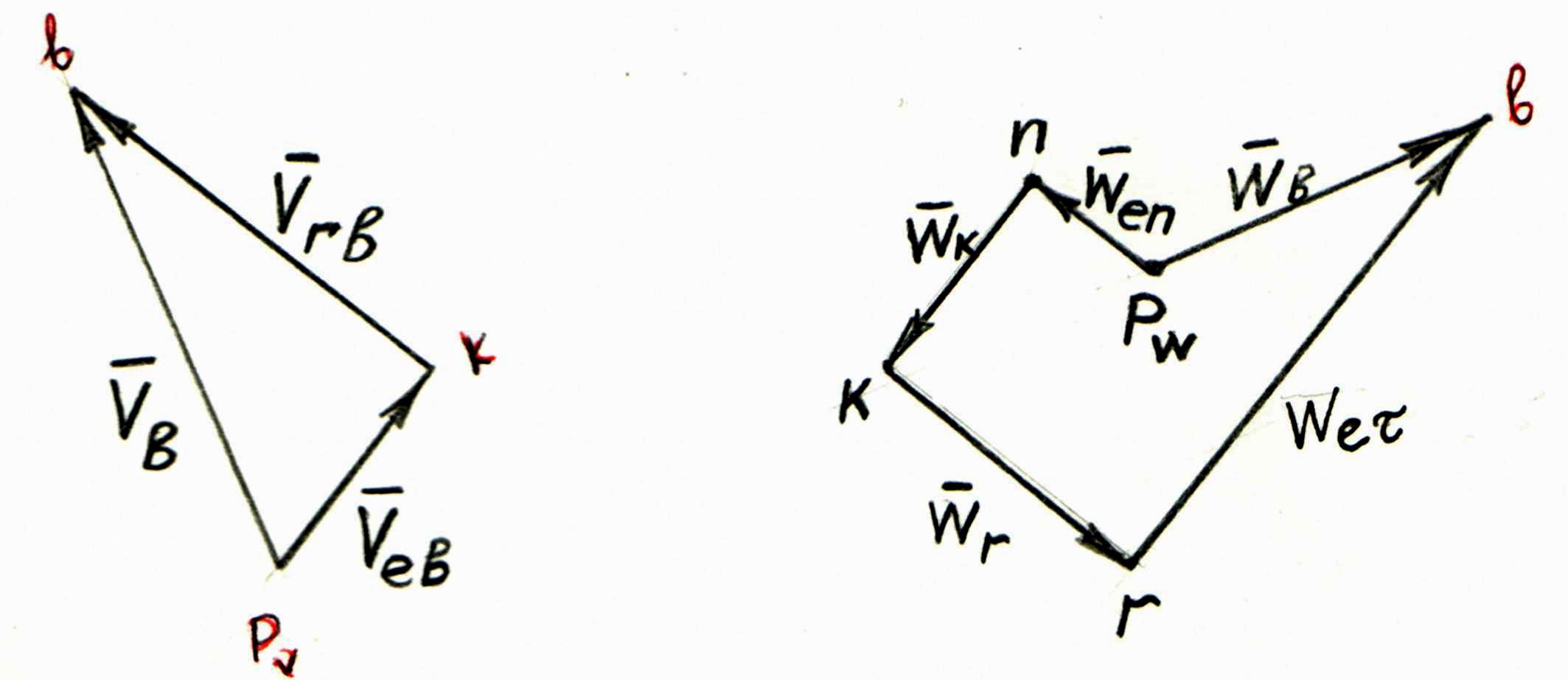
Строим план ускорений мальтийского механизма. При рассмотрении ускорения точки В, принадлежащей кресту, следует учесть, что при переносном вращательном движении и относительном перемещении вдоль паза возникает также ускорение Кориолиса. Поэтому построение плана ускорений ведем по следующему уравнению

,

где – вектор абсолютного ускорения, равный нормальному ускорению точки В (при ), принадлежащей кривошипу, равный по модулю и направленный по АВ от точки В к точке А; – вектор нормального ускорения в переносном вращательном движении точки В, принадлежащей кресту, равный по модулю и направленный от точки В к точке С; – вектор касательного ускорения в переносном движении, направленный перпендикулярно СВ; – вектор относительного ускорения точки В, направленный вдоль паза креста по СВ; – вектор ускорения Кориолиса, равный по модулю и имеющий направление вектора , повернутого на в направлении угловой скорости (см. рис.7, а,в).

Выполним построение плана ускорений по векторному уравнению, в котором известны векторы по направлениям и модулям. Для векторов известны лишь линии их действия.

От полюса откладываем отрезок , который изображает на плане в определенном масштабе вектор . Масштабный коэффициент ускорений . показывает, сколько единиц ускорения в приходится на 1мм отрезка . Далее из полюса строим отрезок , изображающий вектор в том же масштабе, и через точку п проводим отрезок пк перпендикулярно , который изображает вектор ускорения Кориолиса . Так как известны линии действия векторов , то через точку к проводим прямую, параллельную СВ, а через точку b – прямую, перпендикулярную СВ. Точка их пересечения r дает конец вектора и начало вектора .

Определим модуль вектора из плана с учетом масштабного коэффициента, т.е. ( ). Затем вычислим угловое ускорение

( ).

При построении плана ускорений для первого положения мальтийского механизма обратим внимание на то, что , , и что для третьего положения , , .

Методика построения планов скоростей и ускорений звеньев механизмов приведена в [1], с.70. . .72, 75. . .80; [3], с.33. . .38; [4], с.79. . .96.