3. Решение прямоугольных и четвертных сферических треугольников.

Прямоугольные и четвертные сферические треугольники являются частным случаем косоугольных сферических треугольников.

Прямоугольным сферическим треугольником называется такой сферический треугольник, у которого один из углов равен 90°.

Четвертным сферическим треугольником называется такой сферический треугольник, у которого одна из сторон равна 90°.

К этим треугольникам применимы все правила и алгоритмы решения косоугольных сферических треугольников.

Прямоугольные треугольники можно решать по основным формулам сферической тригонометрии. Так как один из углов равен 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Но более рационально производить решение по правилам Модюи-Непера, почти полностью исключающим промежуточные преобразования, а значит и ускоряющим решение ().

Правила Модюи-Непера формулируются следующим образом:

1. В прямоугольном сферическом треугольнике косинус любого среднего элемента равен произведению котангенсов крайних смежных с ним элементов.

2. Косинус отдельно лежащего элемента сферического треугольника равен произведению синусов двух не смежных с ним рядом лежащих элементов.

В обоих правилах принято, что катеты лежат рядом друг с другом и вместо катетов надо брать их дополнения до 90°.

Формул такого вида 10. Все они однотипны, поэтому для примера приведём четыре характерных:

П

( 3.0)

ри А=90°

cos a = ctg B ctg C

cos B = ctg a ctg (90° – c)

( 3.0)

cos (90° – c) = sin C sin a

cos a = sin (90° – b) sin (90° – c)

Следовательно, в задаче на прямоугольный треугольник, надо задать два элемента и указать, какой угол равен 90°.

П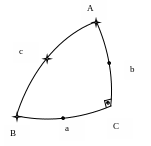 ример 3.8

Дано: а=34°27,3′; b=75°18,6′ C=90°

Найти: A, B, c.

1. Выполняем схематический чертёж и помечаем данные и искомые элементы.

2. Подбираем необходимые формулы.

(по основным формулам сферической тригонометрии)

A, B – формула котангенсов;

c – формула косинуса стороны;

1. ctg A sin C = ctg a sin b – cos b cos C

2. ctg B sin C = ctg b sin a – cos a cos C

3. cos c = cos a cos b + sin a sin b cos C

3. Преобразовываем формулы и производим анализ на знаки. После преобразований независимо от первоначальных формул результат одинаков.

Так как С=90°

+ +

ctg A = ctg a sin b

+ +

ctg B = ctg b sin a

+ +

cos c = cos a cos b

(по правилам Модюи-Непера)

по 1 правилу:

cos (90 – a) = ctg B ctg (90 – b)

cos (90 – b) = ctg A ctg (90 – a)

по 2 правилу:

cos c = sin (90 – b) sin (90 – a)

Откуда: + +

ctg A = ctg a sin b

+ +

ctg B = ctg b sin a

+ +

cos c = cos a cos b

а<90° ctg a, cos a и sin a (+), b<90° sin b, cos b и ctg b (+)

Так как во всех формулах результат положителен, все искомые величины находятся в первой четверти.

4. Составляем схему вычислений и производим вычисления с использованием таблиц 5-а МТ-75(63). Подробности использования таблиц приведены в пояснениях к таблицам. Что бы не менять наименования функций для аргументов больших 90° при входе в таблицу берём их дополнения до 180°. Схема и результаты вычислений приведены в Таблица 3 .7.

Таблица 3.7

	lg		lg		lg
a=34°27.3′ b=75°18.6′	ctg sin	0.16360 9.98557	sin ctg	9.75263 9,41856	cos cos	9.91623 9.40413
	ctg A	0.14917	ctg B	9.17119	cos c	9.32036
	A	35°20.9′	B	81°31,8′	c	77°55,8′
	A=35°20.9′		B=81°31,8′		c=77°55,8′

5. Производим контроль вычислений по теореме синусов. Проверку можно производить как на калькуляторе, так и при помощи таблиц логарифмов.

Не забываем, что отношение, это разность логарифмов

lg sin A = 9.76234 lg sin B = 9.99528 lg sin С =10,00000

l g sin a = 9.75263 lg sin b = 9.98557 lg sin c = 9.99029

0,00971 0.00971 0.00971

Четвертные сферические треугольники, как и прямоугольные можно решать по основным формулам сферической тригонометрии. Т.к. одна из сторон равна 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Возможен и другой путь решения: свести четвертной треугольник к полярному прямоугольному и производить решение по правилам Модюи-Непера.

Сферические треугольники ABC и A₁B₁C₁ называются полярными, если их стороны и углы связаны следующими соотношениями:

A + a₁ = 180°; a + A₁ = 180°;

B + b₁ = 180°; b + B₁ = 180°;

C + c₁ = 180°; c + C₁ = 180°,

т.е. сумма угла данного треугольника с противоположной стороной полярного ему треугольника равна 180°.

П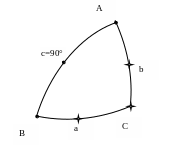 ример 3.9

Дано: a =31°15.2′, C = 120°15.4′

c = 90°

Найти: A, B, b

1. Выполняем схематический чертёж и помечаем данные и искомые элементы.

2. Подбираем необходимые формулы. (по основным формулам сферической тригонометрии)

A – теорема синусов

B – формула котангенсов;

c – формула косинуса стороны;

1. 

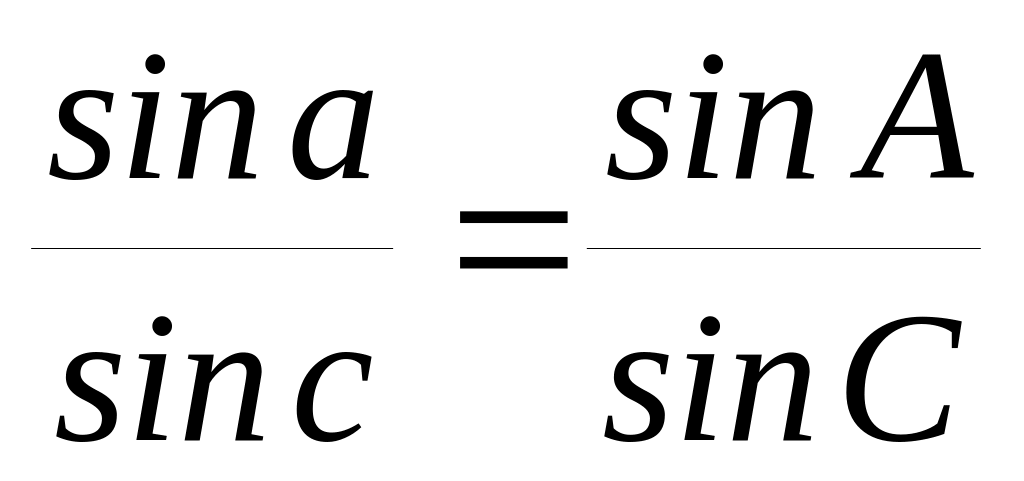
2. ctg B sin C = ctg b sin a – cos a cos C

3. cos c = cos a cos b + sin a sin b cos C

3. Преобразовываем формулы, отделяем неизвестные, а так же производим анализ формулы на знаки.

Так как с = 90°

1. sin A = sin a sin C

+ –

2. tg B = - cos a tg C

+ –

3. tg b = - ctg a sec C

а<90° ctg a, cos a и sin a (+), C>90° sin C (+), sec C и tg C ( – )

Так как во всех формулах результат положителен, все искомые величины находятся в первой четверти.

4. Составляем схему вычислений и производим вычисления с использованием таблиц 5-а МТ-75(63) Таблица 3 .8. Подробности использования таблиц приведены в пояснениях к таблицам. Что бы не менять наименования функций для аргументов больших 90° при входе в таблицу берём их дополнения до 180°.

Таблица 3.8

	lg		lg		lg
a=31°15.2′ C=120°15.4′	sin sin	9.71502 9.93640	cos tg	9.93191 0.23408	ctg sec	0.21687 0.29768
	sin A	9.65142	tg B	0.16599	tg b	0.51455
	A	26°37.5′	B	55°41.5′	b	72°59,8′
	A=26°37.5′		B=55°41.5′		b=72°59,8′

5. Производим контроль вычислений по теореме синусов. Проверку можно производить как на калькуляторе, так и при помощи таблиц логарифмов¹.

lg sin a = 9.71502 lg sin b = 9.98059 lg sin с =10.00000

lg sin A = 9.65142 lg sin B = 9.91699 lg sin C = 9.93640

0.06360 0.06360 0.06360