2. Преобразования угловых (дуговых) величин.

В своей работе судоводитель постоянно имеет дело с различными угловыми величинами. Поэтому он должен уметь быстро и точно переходить от одного вида единиц к другому.

Существует две системы измерения дуг и углов. В первой системе измерение производится в частях окружности. К этой системе относятся три вида единиц:

1. Градусная:

единица измерения – градус (°), равный 1/360 части окружности

доли градуса – минута (′), равная 1/60 части градуса

доли минуты – секунда (′′), равная 1/60 части минуты или

1/3600 части градуса

2. Часовая:

единица измерения – час (^ч), равный 1/24 части окружности

доли часа – часовая минута (^м), равная 1/60 части часа

Доли минуты – часовая секунда (^с), равная 1/60 части минуты или 1/3600 части часа.

3. Румбовая:

единица измерения – румб, равный 11.25°, или 1/32 часть окружности.

Переход от одних единиц к другим легко осуществляется при помощи следующих соотношений:

360°=24^ч; 15°=1^ч 15′=1^м 15′′=1^с

1°=4^м 1′=4^с

0,1°=6′ 0,1′=6′′

Пример 2.4

Дано: долгота в градусах, минутах градуса =36°21,7′E^st

Найти: долготу, выраженную в часах, минутах, секундах

1. Переводим градусы, минуты в градусы 36°21,7′=36°+21,7′/60=36.361667°

2. Переводим градусы в часы: 36.361667°/15=2.424111^ч

3. Отделяем от часов десятичную часть и переводим в минуты 0,424111*60=25.44667^м

4. Отделяем от минут десятичную часть и переводим в секунды 0,44667*60=26,8 ^с≈27^с

Ответ: 2^ч25^м27^с

Во второй системе единиц угол или дуга измеряются в частях радиуса окружности. Это так называемая радианная мера углов. За единицу измерения углов в радианной мере принимается угол, стягивающий дугу длинна которой равняется радиусу. Эта единица называется радианом - рад.

Для перехода из одной системы в другую используются следующие соотношения:

1 рад=180°/°°

1°=1/57.29578=0.01745329 рад, эту величину называют arc 1°

соответственно

arc 1′=1/(57.29578*60)=0,00029089

arc 1′′=1/(57.29578*60*60)=0,00000485

Радианную меру удобно использовать при расчётах на ПК. В табличном процессоре EXCEL предусмотрены функции РАДИАНЫ(..) - для перевода градусов в радианы и ГРАДУСЫ(..) для обратного перевода.

Переход между системами можно осуществлять при помощи специальных таблиц. В МТ-63 это таблицы 38 и 39.

Пример 2.5

Дано: Часовой угол в градусах, минутах дуги t=127°31.8′

Найти: значение в радианной мере

1. Переводим градусы, минуты в градусы 127°31.8′=127°+31.8′/60=127,53°

2. Переводим градусы в радианы 127,53°/57,3= 2.225654рад

Пример 2.6

Дано: Азимут в радианной мере А=1,86357рад

Найти: значение в градусной мере

1. Переводим радианы в градусы 1,86357рад*57,3=106.7826°

2. Переводим градусы в градусы, минуты

А=106,7826°=106°(0,7826*60)′=106°46,0′

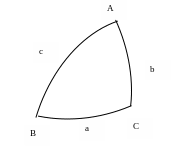
3. Решение сферических треугольников.

1. Основные формулы сферической тригонометрии

Для решения многих задач судовождения используются формулы сферической тригонометрии. На основе таких формул составляются, например, уравнения изолиний и градиентов некоторых навигационных параметров; задачи на определение места судна; определяются величины углов и сторон параллактического треугольника с целью получения координат места судна и поправки компаса методами мореходной астрономии и многого другого.

Задачей сферической тригонометрии является установление зависимостей между сторонами и углами сферического треугольника. Сферический треугольник считается заданным, если известны какие-либо три его элемента. Под решением треугольника понимают определение неизвестных его элементов. В большинстве случаев решение выполняется по так называемым основным формулам, к которым относятся:

• формула (теорема) косинуса стороны;

• формула (теорема) косинуса угла;

• формула (теорема) синусов;

• формула котангенсов, называемая так же формулой четырёх рядом лежащих элементов;

• формула пяти элементов.

В некоторых случаях возникает необходимость использования дополнительных формул, к которым относятся:

• формулы полупериметра;

• формулы Деламбра-Гаусса;

• аналогии (пропорции) Непера.

Эти группы формул имеют некоторые преимущества:

1. логарифмируются, поэтому не требуют применения таблиц сумм и разностей;

2. искомые углы получаются по самым выгодным функциям – тангенсам, т.е. дают наименьшие ошибки при вычислении угла;

3. в ыбор четверти искомых углов происходит уже в решении, следовательно, отпадает необходимость анализа формулы на знаки.

Формула косинуса стороны (теорема косинусов): в сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих сторон на косинус угла между ними.

Формула косинуса стороны связывает стороны и один из углов сферического треугольника. Всего этих формул три:

c os a = cos b cos c + sin b sin c cos A

cos b = cos a cos c + sin a sin c cos B ( 3.0)

cos c = cos a cos b + sin a sin b cos C

Формула косинуса угла (теорема косинусов для полярного треугольника): в сферическом треугольнике косинус угла равен отрицательному произведению косинусов двух других углов плюс произведение синусов этих углов на косинус стороны между ними.

Ф ормула косинуса угла связывает углы и одну из сторон сферического треугольника. Всего этих формул так же три:

cos А = - cos B cos C + sin B sin C cos a

cos B = - cos A cos C + sin A sin C cos b ( 3.0)

cos C = - cos A cos B + sin A sin B cos c

Формула котангенсов (формула четырёх рядом лежащих элементов): произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов.

Формула связывает четыре элемента лежащих подряд.

c tg A sin B = ctg a sin c – cos c cos B

ctg A sin C = ctg a sin b – cos b cos C

ctg B sin A = ctg b sin c – cos c cos A ( 3.0)

ctg B sin C = ctg b sin a – cos a cos C

ctg C sin A = ctg c sin b – cos b cos A

ctg C sin B = ctg c sin a – cos a cos B

Формула синусов (теорема синусов): в сферическом треугольнике синусы сторон пропорциональны синусам противолежащих углов.

( 3.0)

Аналогии Непера:

( 3.0)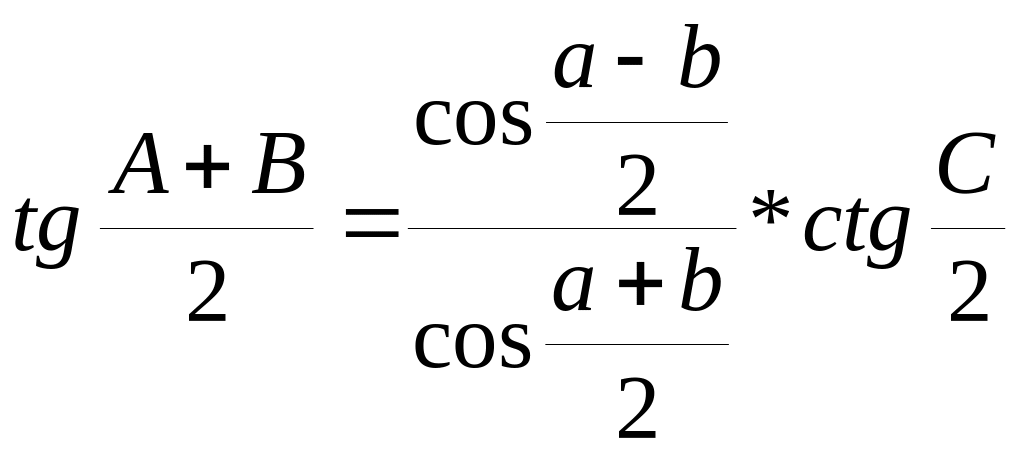

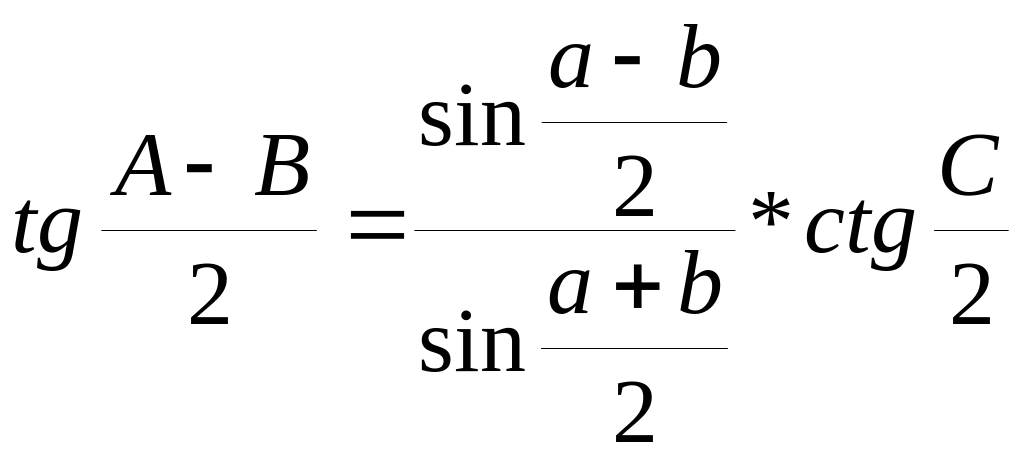
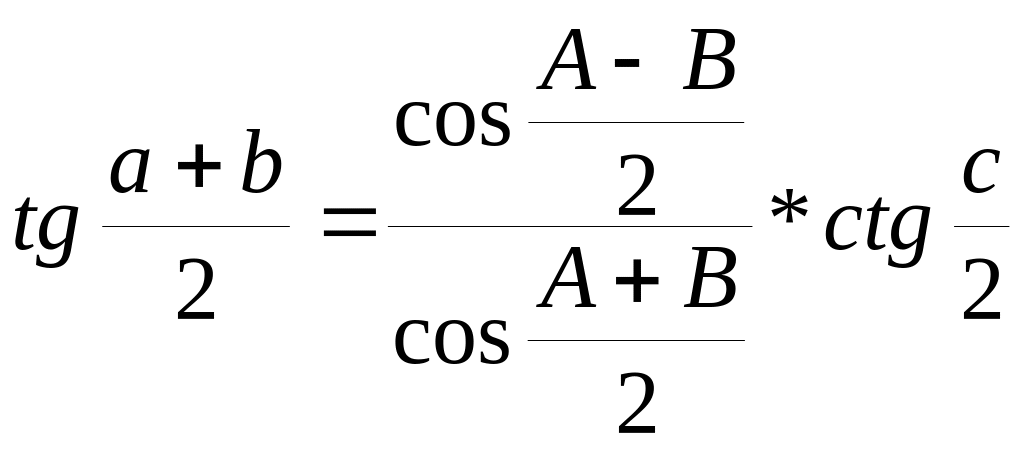
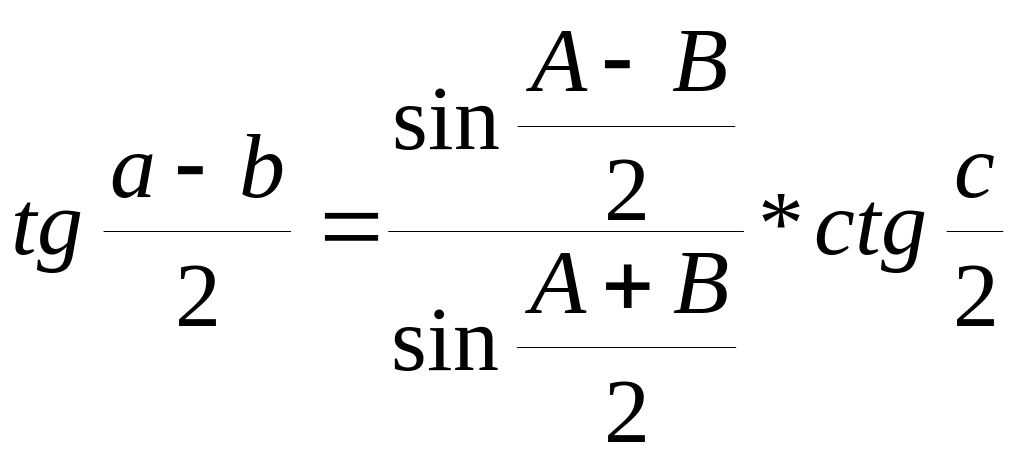
По аналогиям Непера в сочетании с теоремой синусов обычно производится решение двух типов задач на косоугольный сферический треугольник – когда известны две стороны и противолежащий одной из них угол, или два угла и противолежащая одному из них сторона. Как уже указывалось выше, применение этих типов формул позволяет отыскивать неизвестные элементы без применения логарифмов сумм и разностей. Однако применение только этих двух групп формул приводит к необходимости при расчёте некоторых неизвестных элементов использовать ранее найденные элементы.

Чтобы не использовать ранее найденные элементы последних двух типов задач, можно воспользоваться следующим алгоритмами:

Когда известны две стороны и противолежащий одной из них угол, например a, b, A, вычисляются вспомогательные величины G и H:

ctg G = cos A tg b

tg H = tg A cos b

После чего вычисляются неизвестные величины по формулам:

s in B = sin A sin b cosec a

sin (c-G) = cos a sec b sin G ( 3.0)

sin (C+H) = ctg a tg b sin H

Когда известны два угла и противолежащая одному из них сторона, вычисляют вспомогательные величины K и M:

ctg K = cos a tg B

tg M = tg a cos B

После чего вычисляются неизвестные величины по формулам:

s in b = sin a sin B cosec A

sin (C-K) = cos A sec B sin K ( 3.0)

sin (c+M) = ctg A tg B sin M