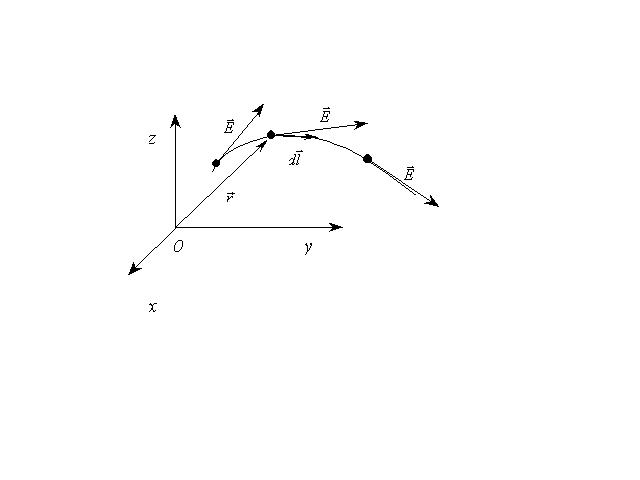
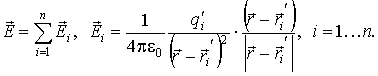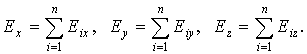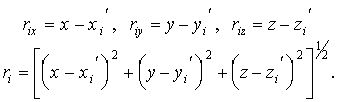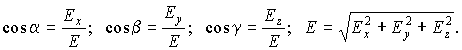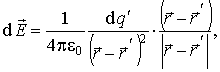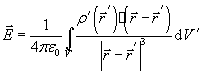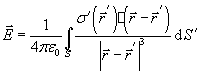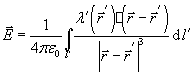- •Дивергенция
- •Определение
- •[Править]Определение в декартовых координатах
- •[Править]Физическая интерпретация
- •[Править]Геометрическая интерпретация
- •[Править]Дивергенция в физике
- •[Править]Свойства
- •Теорема о циркуляции
- •Закон сохранения заряда в интегральной форме
- •Закон сохранения заряда в дифференциальной форме
- •Напряжённость электрического поля точечного заряда [править]Для системы си
- •.2. Принцип суперпозиции для вектора напряженности электростатического поля
- •Диэлектрическая проницаемость
- •Потенциальная энергия
- •Поляризация диэлектриков
- •18.2. Вывод закона Ома в дифференциальной форме в классической электронной теории
- •Законы Кирхгофа
- •Формулировка
- •[Править]Первый закон
- •[Править]Второй закон
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
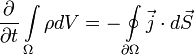
Здесь ![]() —
некоторая произвольная область в
трёхмерном пространстве,
—
некоторая произвольная область в
трёхмерном пространстве, ![]() —
граница этой области,
—
граница этой области, ![]() —
плотность заряда,
—
плотность заряда, ![]() —плотность
тока (плотность
потока электрического заряда) через
границу.
—плотность
тока (плотность
потока электрического заряда) через
границу.
Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)
![]()
Напряжённость
электри́ческого по́ля — векторная физическая
величина, характеризующаяэлектрическое
поле в
данной точке и численно равная
отношению силы ![]() действующей
на пробный
заряд,
помещенный в данную точку поля, к величине
этого заряда
действующей
на пробный
заряд,
помещенный в данную точку поля, к величине
этого заряда ![]() :
:
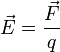 .
.
Также иногда называется силовой характеристикой электрического поля.
Математически
зависимость вектора ![]() от
координат пространства сама задаёт векторное
поле.
от
координат пространства сама задаёт векторное
поле.
Модуль напряжённости электрического поля в СИ измеряется в В/м (Вольт на метр)
Напряжённость электрического поля точечного заряда [править]Для системы си
Используя потенциалы
![]()
К
примеру, для точечного заряда, исходя
из закона
Кулона ![]() Так
как эквипотенциальные
поверхности являются
в этом случае сферами, то производная
по нормали есть производная по радиусу.
Таким образом мы можем прийти к так
называемому кулоновскому полю:
Так
как эквипотенциальные
поверхности являются
в этом случае сферами, то производная
по нормали есть производная по радиусу.
Таким образом мы можем прийти к так
называемому кулоновскому полю:
![]() .
.
В силу центральной симметрии поля точечного заряда:
![]() .
.
.2. Принцип суперпозиции для вектора напряженности электростатического поля
Напряженность
электрического (электростатического)
поля ![]() ,
образованного единичным точечным
зарядом
,
образованного единичным точечным
зарядом ![]() ,
определена соотношением (1.1).
Если в системе имеется
,
определена соотношением (1.1).
Если в системе имеется ![]() электрических
точечных зарядов
электрических
точечных зарядов ![]() ,
то напряженность результирующего
поля
,
то напряженность результирующего
поля ![]() определяется
как сумма напряженности полей
определяется
как сумма напряженности полей ![]() ,
образованных каждым из зарядов в
отдельности:
,
образованных каждым из зарядов в
отдельности:
|
(1.2) |
|
|
||
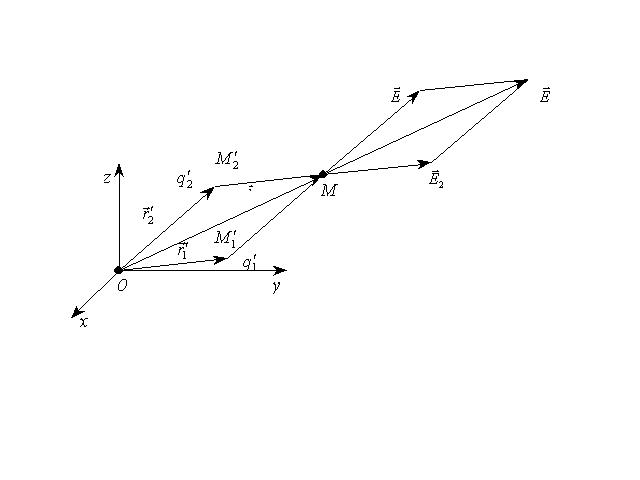
Рис. 1.2. Принцип суперпозиции для вектора напряженности электростатического поля |
Здесь ![]() -
радиус-вектор точки наблюдения,
-
радиус-вектор точки наблюдения, ![]() -
радиус-вектор точки расположения
электрического заряда
-
радиус-вектор точки расположения
электрического заряда ![]() .
.
Сложение в выражении (1.2) выполняется по правилу треугольника или параллелограмма, "геометрически", по правилу сложения векторных величин, то есть по-координатно:
|
(1.3) |
При
вычислении проекций вектора
на
оси декартовых координат удобно
через ![]() обозначить
координаты точки наблюдения, а через
обозначить
координаты точки наблюдения, а через ![]() с
индексом
с
индексом ![]() -
номер электрического заряда - координаты
заряда
-
номер электрического заряда - координаты
заряда ![]() .
.
В этом случае имеют место соотношения:
|
(1.4) |
Для
направляющих косинусов вектора ![]() имеем:
имеем:
|
(1.5) |
Еще раз подчеркнем, что при сложении электрических полей отдельно "складываются" проекции вектора и только потом вычисляется модуль полученного вектора.
Непрерывное распределение электрических зарядов.
В
практически интересных случаях суммарный
электрический заряд
можно
считать распределенным по известному
закону по конечному или бесконечному
объему, поверхности или вдоль
пространственной линии. В этих случаях
удобно ввести - объемную
плотность электрического заряда ![]() :
:
|
(1.6) |
где ![]() -
элемент объема (дифференциал объема)
рассматриваемого тела,
-
элемент объема (дифференциал объема)
рассматриваемого тела, ![]() -
электрический заряд этого элемента;
-
электрический заряд этого элемента;
- поверхностную
плотность электрического заряда ![]() :
:
|
(1.7) |
где ![]() -
элемент площади поверхности,
-
электрический заряд этого элемента;
-
элемент площади поверхности,
-
электрический заряд этого элемента;
- линейную
(погонную) плотность электрического
заряда ![]() :
:
|
(1.8) |
где ![]() -
элемент длины пространственной кривой.
-
элемент длины пространственной кривой.
Величины ![]() ,
и
являются
физически бесконечно малыми величинами,
поэтому элементарные заряды
можно
считать точечными. Поле точечного
электрического заряда известно:
,
и
являются
физически бесконечно малыми величинами,
поэтому элементарные заряды
можно
считать точечными. Поле точечного
электрического заряда известно:
|
(1.9) |
здесь ![]() -
дифференциал напряженности электрического
поля в точке наблюдения с радиусом-вектором
-
дифференциал напряженности электрического
поля в точке наблюдения с радиусом-вектором ![]() ,
создаваемого элементарным зарядом
,
расположенным в точке с радиусом-вектором
,
создаваемого элементарным зарядом
,
расположенным в точке с радиусом-вектором ![]() .
Величина
определена
одним из выражений (1.6), (1.7) или (1.8).
Остается только просуммировать
выражение (1.9) по
всем элементарным зарядам системы.
Формальное решение задачи имеет вид:
.
Величина
определена
одним из выражений (1.6), (1.7) или (1.8).
Остается только просуммировать
выражение (1.9) по
всем элементарным зарядам системы.
Формальное решение задачи имеет вид:
|
(1.10) |
для заряженного объема,
|
(1.11) |
для заряженной поверхности,
|
(1.12) |
для
заряженной линии конечных или бесконечных
размеров. В
выражениях (1.10), (1.11) и (1.12) интегрирование
проводится по "штрихованным"
переменным, координаты точки
наблюдения
или ![]() играют
при этом роль параметров.
играют
при этом роль параметров.
Физический смысл соотношений (1.2), (1.10), (1.11) и (1.12) состоит в том, что при известном расположении зарядов в пространстве (дискретное или непрерывное распределение) напряженность электрического поля может быть вычислена для произвольной точки пространства.
Читателям,
не владеющим понятиями объемного,
поверхностного и (или) линейного
интеграла, можно посоветовать пользоваться
формулами (1.2).
При этом роль величин
будут
играть произведения ![]() ,
, ![]() и
(или)
и
(или) ![]() ,
где
,
где ![]() ,
, ![]() и
(или)
и
(или) ![]() должны
выбираться достаточно малыми, чтобы
каждый из описанных электрических
зарядов можно было бы считать точечным.
Последнее выполняется, если характерный
линейный размер элемента объема, элемента
площади поверхности или элемента длины
будет значительно меньше расстояния
от этого элемента до точки наблюдения.
должны
выбираться достаточно малыми, чтобы
каждый из описанных электрических
зарядов можно было бы считать точечным.
Последнее выполняется, если характерный
линейный размер элемента объема, элемента
площади поверхности или элемента длины
будет значительно меньше расстояния
от этого элемента до точки наблюдения.
|