3.6. Квантовомеханическая модель атома водорода

Квантовая физика дает для атома водорода такое же решение для значений энергии атома, что и теория Бора, но она боле последовательна и описывает не только излучение атома водорода.

Стационарное уравнение Шредингера для атома водорода имеет вид:

Решения этого уравнения для любого положительного значения энергии соответствует пролету электрона около ядра и удалению в бесконечность, что не соответствует определению атома, как динамически устойчивой системы.

Решения, соответствующие дискретным отрицательным значениям энергии, равной

, n = 1,2,3,…

соответствуют электрону, связанному с ядром.

При n = 1 получим значения энергии в основном состоянии атома водорода эВ.

Так как электрон в атоме водорода движется в центрально-симметричном поле ядра, то оператор Лапласа и собственные волновые функции удобно записывать в сферической системе координат

.

Собственные волновые функции содержат 3 целочисленных параметров n, l, m_ℓ , которые называются квантовыми числами.

Число n – главное квантовое число. Оно определяет уровни энергии электрона в атоме.

ℓ – азимутальное или орбитальное квантовое число, оно определяет модуль орбитального момента импульса ).

m_ℓ – магнитное квантовое число, оно определяет проекцию орбитального момента импульса на некоторое направление z, определяемое внешним магнитным полем)

.

n = 1, 2, 3,…. При данном n ℓ = 0, ±1, ±2, ±3, … ±(n – 1).

При данных n и ℓ m_ℓ = 0,  1, 2, …, ℓ.

Энергетическое состояние электрона определяется только квантовым числом n. Решения, удовлетворяющие стандартным условиям, получаются при значениях l , не превышающих n – 1

- всего n значений

При данном ℓ квантовое число m может принимать 2ℓ + 1 различных значений

.

Состояния атома с одинаковой энергией (одинаковым квантовым числом n), отличающиеся числами l и m, называются вырожденными состояниями.

Число различных состояний называется кратностью вырождения.

Так как для данного n , а m может принимать , значение , то кратность вырождения водородного атома:

Таким образом, каждому значению E_n соответствует несколько собственных функций , отличающихся числами ℓ и m_ℓ..

Состояние электрона с ℓ = 0 называют S – состоянием,

ℓ= 1 - p – состоянием,

ℓ = 2 - d, ℓ = 3 - f, ℓ = 4 - g, ℓ = 5 - h.

Так как , то возможны следующие состояния:

1S

2S 2P

3S 3P 3d

4S 4P 4d 4f

В квантовой механике доказывается, что для орбитального вантового числа имеется правило отбора

Это значит, что возможны такие переходы, при которых ℓ изменяется на единицу.

Поэтому для серии Лаймана )

Бальмера

При увеличении числа n дискретность энергетических уровней уменьшается и характер поведения частицы приближается к классическому. В этом состоит принцип соответствия:

При больших квантовых числах следствия, вытекающие из квантовой механики, должны совпадать с результатами классической теории.

Подобно тому, как при релятивистская механика переходит в ньтоновскую, при квантовая механика переходит к классическому описанию (пренебрегаем ).

Собственные функции распадаются на два множителя:

,

- вещественный,

- комплексный.

Так как координаты r, независимы, то при подстановке в уравнение Шредингера в сферических координатах уравнение Шредингера разбивается на две независимые части.

Первое уравнение Шредингера для радиальной части

и для сферической части

Первое уравнение зависит только от вида потенциальной энергии, а следовательно определяется конкретной физической природой взаимодействия частиц (для нашего случая – кулоновского).

Второе уравнение не зависит от вида силового поля, поэтому его решение одинаково для всех центрально-симметричных полей.

Условие нормировки для этих уравнений имеет вид в сферических координатах:

- телесный угол

Из решения этих уравнений можно сделать следующие выводы:

1) Электрон может иметь в атоме водорода лишь дискретные значения энергия:

, n = 1, 2, 3,…

2) Состояние электрона в атоме характеризуется набором 4 квантовых чисел

а) главного квантового числа n, определяющего энергию электрона;

б) орбитальное квантовое числа ℓ, определяющего дискретное значение модуля орбитального момента импульса

Магнитного квантового числа m_ℓ, определяющего стационарные ориентации орбитального момента импульса электрона L в пространстве, например, их проекции на направление внешнего магнитного поля .

Диапазону значений ℓ соответствует значений m_ℓ..

Например, если ℓ = 2, то вектор орбитального момента импульса электрона в атоме может принимать в пространстве дискретных ориентаций .m_ℓ = 0, ±1, ±2.

г) спинового квантового числа s, определяющего ориентацию собственного момента импульса электрона (спина).

Собственный механический момент электрона определяется

, где .

Проекция собственного механического момента равна

.

Полный механический момент электрона складывается из спинового и орбитального моментов электрона

, j = ℓ + s, ℓ + s-1, │ℓ-s│,

j – квантовое число полного момента импульса.

Проекция полного механического момента

В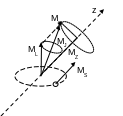 заимодействие орбитального и магнитного момента (как взаимодействие магнитных стрелок) приводит к расщеплению энергетических уровней, а следовательно, спектральных линий. Оно называется спин-орбитальным взаимодействием.