
- •Численные методы
- •Тема 1. Приближенные числа и действия над ними.
- •Тема1. Приближенные числа и действия над ними.
- •Тема 2. Приближенные решения алгебраических и трансцендентных уравнений.
- •Тема 2. Приближенные решения алгебраических и трансцендентных уравнений.
- •Тема 3. Решение систем линейных алгебраических уравнений.
- •Тема 3. Решение систем линейных алгебраических уравнений.
- •Тема 4. Интерполирование и экстраполирование функций.
- •Тема 4. Интерполирование и экстраполирование функций.
- •Тема 5. Численное интегрирование.
- •Тема 5. Численное интегрирование.
- •Тема 6. Численное решение обыкновенных дифференциальных уравнений.
- •Тема 6. Численное решение обыкновенных дифференциальных уравнений.
- •Тема 7. Численное решение задач оптимизации.
- •Тема 7. Численное решение задач оптимизации.
- •Тема1. Приближенные числа и действия над ними.
Тема 5. Численное интегрирование.
Тема 5. Численное интегрирование.
г
а
а
б
а
а
б
б
а
г
1. Приближенное значение интеграла
![]() (полагая n=5), вычисленное
по формуле левых прямоугольников, равно:
(полагая n=5), вычисленное
по формуле левых прямоугольников, равно:
15;
5;
12,5;
10.
2. Используя метод левых прямоугольников
вычислен определенный интеграл
![]() (полагая
n=4), который приблизительно
равен:
(полагая
n=4), который приблизительно
равен:
1,5744;
1,6024;
1,1053;
1,7845.
3. S =
![]()
![]()
метод Симпсона;
метод трапеций;
формула левых прямоугольников;
формула правых прямоугольников.
4. S ≈
![]()
метод прямоугольников;
метод трапеции;
метод парабол;
метод Симпсона.
5. Приближенное значение интеграла
![]() при n=4, вычисленное по
формуле трапеции, равно:
при n=4, вычисленное по
формуле трапеции, равно:
0,783;
0,5;
0,645;
0,812.
6. Приближенное значение интеграла при h=0,25 , вычисленное по формуле Симпсона, равно:
0,782:
0,702;
0,5;
0,645.
7.
![]()
формула Гаусса;
формула Ньютона─Котеса;
формула Симпсона;
формула Лагранжа.
8. Традиционно при получении квадратных формул Гаусса в исходном интеграле выполняется замена переменной, переводящая интеграл по отрезку [a;b] в интеграл по отрезку:
[b;a];
[-1;1];
[0;1];
[1;2].
9. Система позволяет благодаря графическим возможностям проиллюстрировать геометрический смысл интеграла
Match Cad;
Derive;
Mathematica;
Maple.
10. S ≈![]()
метод трапеции;
метод левых прямоугольников;
метод правых прямоугольников;
метод средних прямоугольников.
Тема 6. Численное решение обыкновенных дифференциальных уравнений.
Тема 6. Численное решение обыкновенных дифференциальных уравнений.
а
б
а
в
в
г
б
а
а
г
1. Если последовательные значения
функции, являющейся решением задачи
Коши для дифференциального уравнения
y´=f(x,y)
с начальными условиями y
(![]() )
=
)
=
![]() , x=
, находятся по методу Эйлера
, x=
, находятся по методу Эйлера
![]() ,
то
,
то
![]() , определяемая уравнением y´=
х + y, при
, определяемая уравнением y´=
х + y, при
![]() и шаге h=0,1 равно:
и шаге h=0,1 равно:
1,1;
2;
1,2;
1,3.
2. Методом Эйлера для дифференциального
уравнения y´=y-x
с начальным условием
![]() на отрезке [0;1,5] при h=0,25
на отрезке [0;1,5] при h=0,25
![]() равно:
равно:
2;
2,28125;
1,45;
4,75275.
3. При интегрировании методом Эйлера
дифференциального уравнения y´=y-x
с начальным условием
![]() на
отрезке [0;1,5] при h=0,25 Δ
равно:
на
отрезке [0;1,5] при h=0,25 Δ
равно:
0,406;
0,25;
0,375;
0,445.
4. Локальная оценка метода Рунге-Кутты 4го порядка точности имеет вид:
| r | ≤ Ch³ ;
| r | ≤ Ch²;
| r | < C
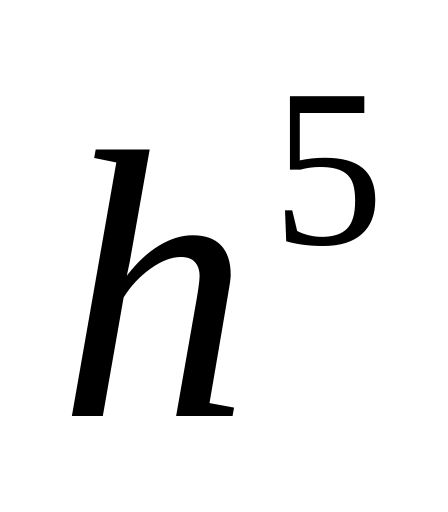 ;
;| r | ≤ C
 .
.
5.
![]()
метод Зейделя;
метод Эйлера;
метод Рунге-Кутта второго порядка;
метод Рунге-Кутта 4го порядка.
6.
![]() , где
i=0,1;…,
, где
i=0,1;…,
метод Зейделя;
метод Эйлера;
метод Рунге-Кутта второго порядка;
метод Рунге-Кутта 4го порядка.
7. Δ![]()
метод Зейделя;
метод Эйлера;
метод Рунге-Кутта второго порядка;
метод Рунге-Кутта 4го порядка.
8. Метод Эйлера
одношаговый метод;
n-шаговый метод;
i-шаговый метод;
многошаговый метод.
9. Метод Рунге-Кутта
одношаговый метод;
n-шаговый метод;
i-шаговый метод;
многошаговый метод.
10. Метод Адамса
одношаговый метод;
n-шаговый метод;
i-шаговый метод;
многошаговый метод.
