8. 8. Заміна змінних в потрійному інтегралі

Нехай області в системі координат відповідає область в системі координат , тоді справедлива формула:

де якобіан має вигляд .

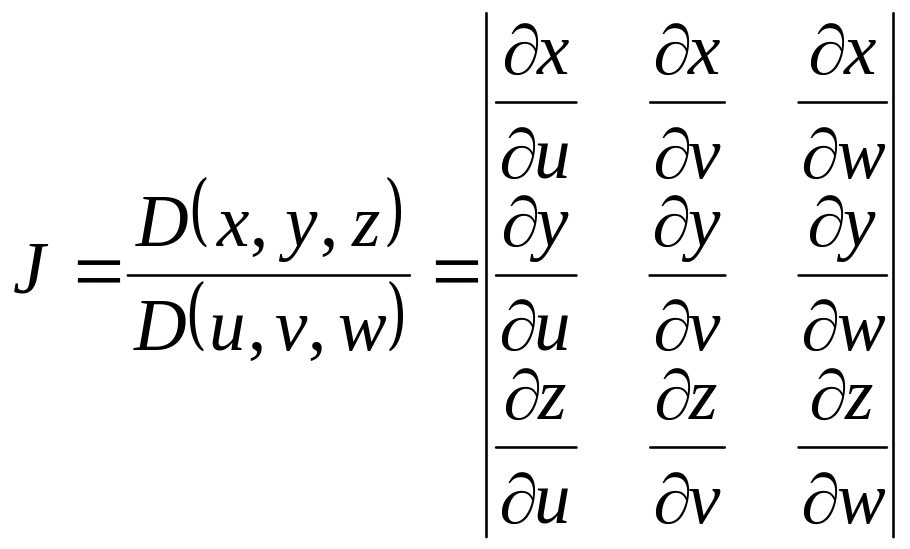Найчастіше використовують циліндричну і сферичну системи координат, а також їх узагальнення.

Циліндрична система координат:

.

Загальні циліндричні координати:

.

Узагальнені циліндричні координати:

.

Сферичні координати:

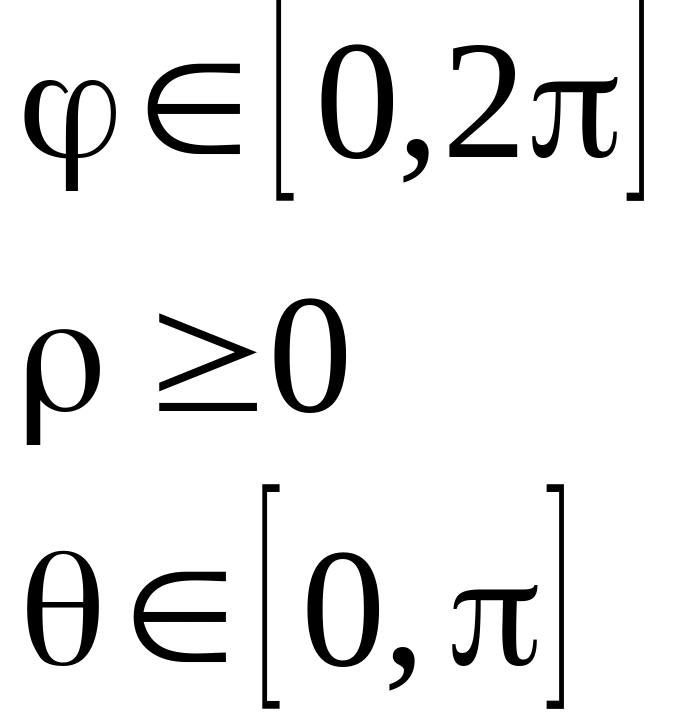
Загальні сферичні координати:

.

Узагальнені сферичні координати:

.

9. 9. Застосування потрійного інтеграла у фізиці

До обчислення потрійних інтегралів приводять задачі, пов'язані з неперервним розподілом маси в просторовій області.

Якщо відома щільність розподілу маси в області простору, то можна одержати формули статичних моментів відносно координатних площин:

, , ;

моментів інерції відносно координатних вісей:

, ,

;

моментів інерції відносно координатних площин:

, ,

;

полярного моменту інерції

;

координат центра мас:

, ,

.

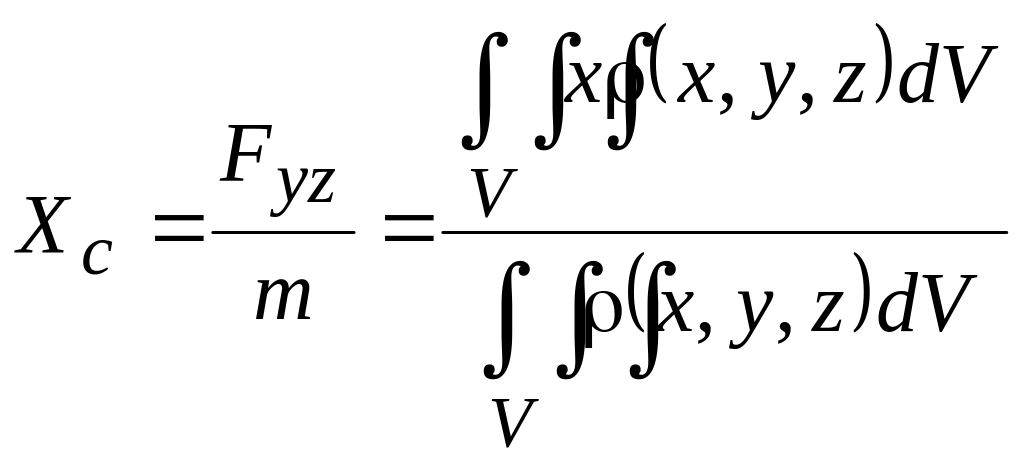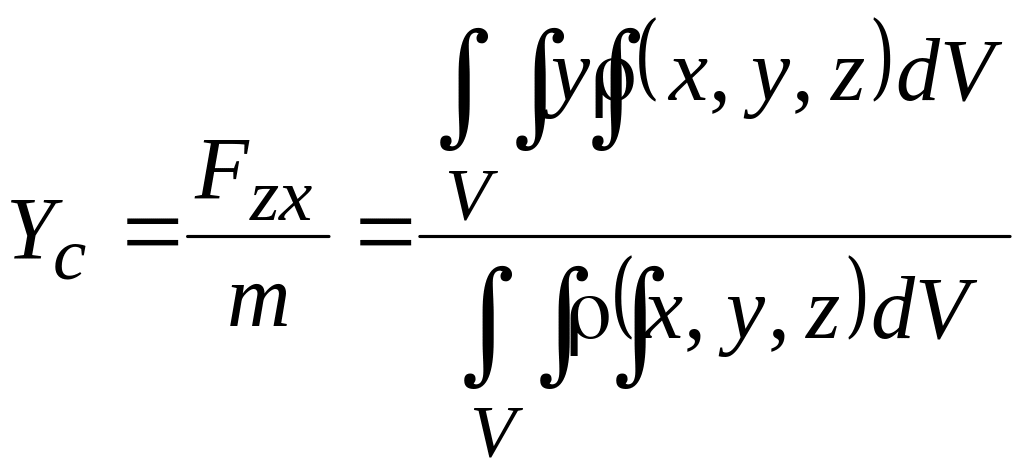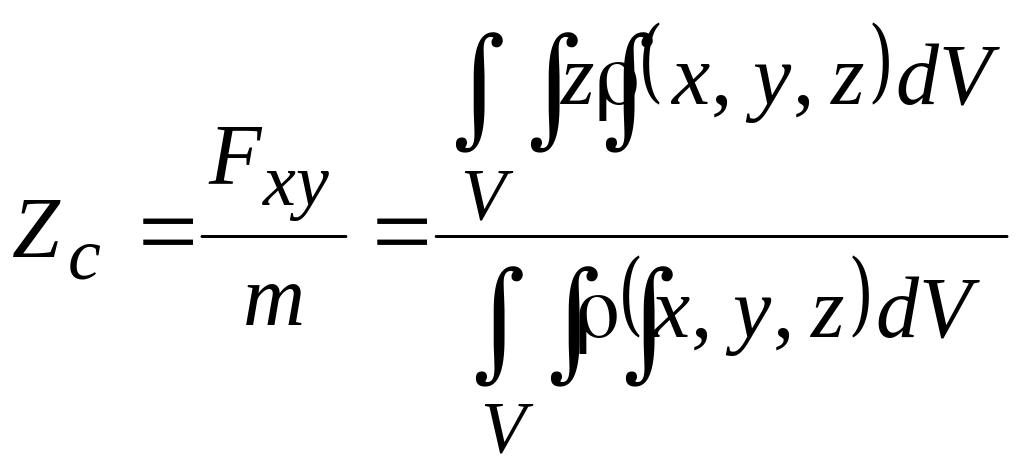Вправи

6.1. Побудувати області, площі яких виражаються інтегралами:

1) ; 2) .

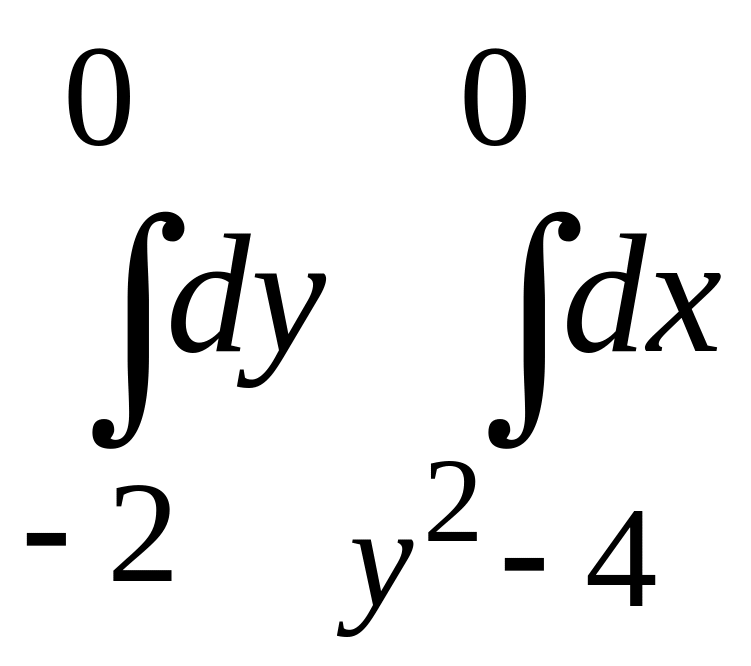Змінити порядок інтегрування й обчислити площі.

6.2. Змінити порядок інтегрування:

а) ;

б) ;

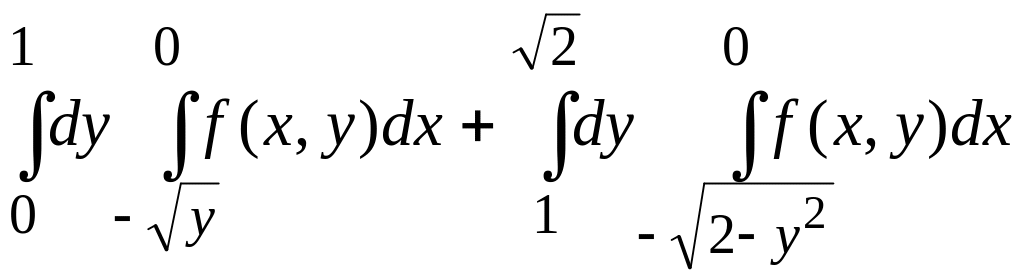в) .

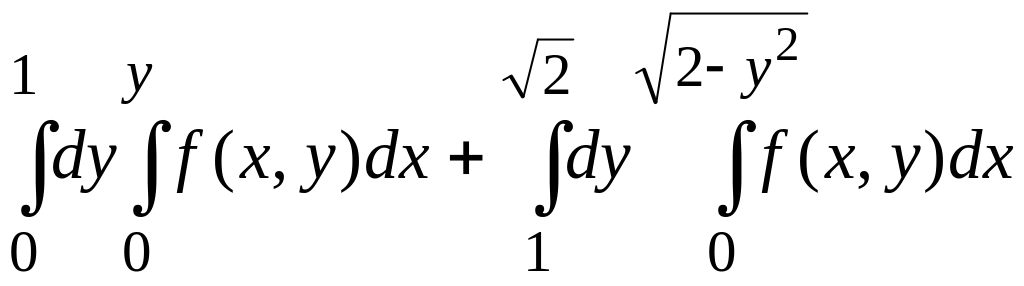6.3. Представити подвійний інтеграл за допомогою повторних із зовнішнім інтегруванням по і по :

а) : , , ;

б) : , ;

в) : , , .

6.4. Обчислити , де – криволінійний трикутник, обмежений параболою і прямими , .

6.5. Обчислити , де – частина кола радіуса a з центром у точці (0;0), що лежить у першій чверті.

6.6. Обчислити інтеграли:

а) , : , ;

б) ;

в) , : , ;

г) , : , ;

д) 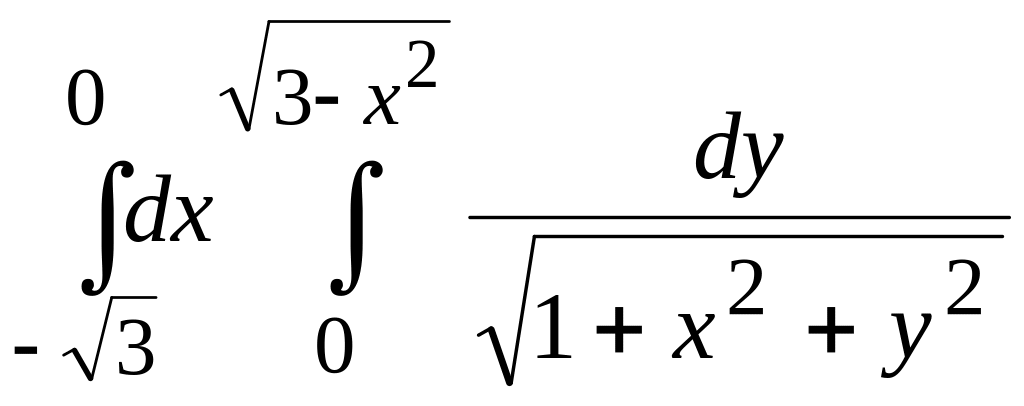; є) .

6.7. Знайти об’єм тіла, обмеженого поверхнями (за допомогою подвійного інтегралу):

а) , , , , ;

б) , , , , ;

в) , , , , , .

6.8. Знайти площу області, яка обмежена кривими:

а) ; б) ; в) .

6.9. Знайти об'єм тіла, обмеженого еліптичним параболоїдом , площиною і координатними площинами.

6.10. Обчислити об'єм тіла, обмеженого площиною , циліндром і конусом .

6.11. Обчислити координати центра ваги фігури, обмеженої кривими:

а) , ;

б) , , ;

в) , ;

г) , , .

6.12. Обчислити:

а) ;

б) , : , , ;

в) , : , , , ;

г) , : , , , ;

д) , : , , , , .

6.13. Обчислити , де – область, обмежена координатними площинами і площиною .

6.14. Знайти об’єм тіла, обмеженого поверхнями:

а) , ;

б) , , ;

в) , , .

6.15. Визначити центр мас однорідного тіла, обмеженого поверхнею і координатними площинами.

6.16. Знайти масу тіла, обмеженого поверхнями:

а) , , , , ;

б) , , , , , ;

в) , , , , .

Розділ 7. Ряди

10. 1. Числові ряди. Основні поняття

Розглянемо числову послідовність , , ..., , ...

Означення 7.1. Рядом називається нескінченна сума числової послідовності

(7.1)

де – члени числової послідовності.

Елемент називається загальним членом ряду. Ряд вважається заданим, якщо відомо закон утворення членів ряду, тобто загальний член ряду .

Наприклад, якщо , маємо ряд .

Для одержуємо ряд .

Суму перших членів ряду називають -ою частинною сумою ряду. Очевидно, що

… .

Частинні суми ряду утворюють послідовність , яка при може мати або не мати границю.

Означення 7.2. Числовий ряд (7.1) називається збіжним, якщо для нього існує скінченна границя послідовності частинних сум, тобто

(7.2)

При цьому, скінченне число називають сумою ряду, тобто для ряду, що є збіжним,

. (7.3)

Якщо або не існує, то ряд називається розбіжним.

Таким чином, щоб встановити, чи є збіжним чи розбіжним даний числовий ряд, потрібно знайти його суму як границю послідовності частинних сум при .

Означення 7.3. Залишком ряду (7.1) називається

(7.4)

тобто .

Приклад 7.1. Дослідити на збіжність числовий ряд

.

Розв’язання. Знайдемо для даного ряду -у частинну суму . Оскільки , то можна записати ряд у вигляді

.

Тоді і .

Отже, даний ряд є збіжним.

Зазначимо, що основною задачею теорії рядів є дослідження збіжності.

Геометричним рядом називають числовий ряд

, (7.5)

члени якого утворюють нескінченну геометричну прогресію зі знаменником .

Приклад 7.2. Дослідити на збіжність геометричний ряд.

Розв’язання. Як відомо, сума перших членів геометричної прогресії дорівнює

. (7.6)

Тоді .

Оскільки одержимо, що

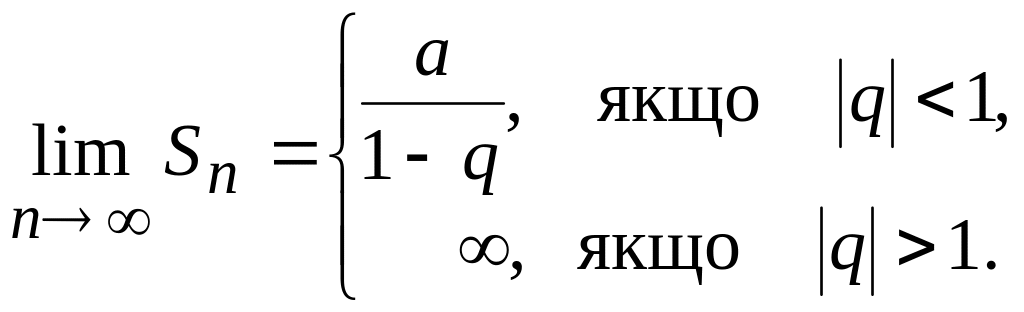
Отже, геометричний ряд є збіжним при , його сума при цьому виражається числом , і є розбіжним, при .

Для випадку одержуємо ряд , сума перших членів якого , отже і ряд є розбіжним. Для випадку одержуємо ряд , для якого

Отже, для цього випадку не існує і ряд є розбіжним.