Статичні моменти.

Аналогічно міркуючи, можна одержати формули для обчислення статичних моментів пластинки відносно координатних осей:

; . (6.13)

Координати центра мас.

У механіці доводиться, що статичний момент пластинки відносно якої-небудь осі збігається зі статичним моментом точкової маси, рівної масі пластинки, зосередженої в центрі ваги її відносно тієї ж осі. Звідси, позначаючи через координати центра мас пластинки , будемо мати:

; .

Отже,

, , (6.14)

Моменти інерції.

Аналогічно, для моментів інерції пластинки одержуємо:

; . (6.15)

Можна показати, що полярний момент пластинки обчислюється за формулою

. (6.16)

Очевидно, що

.

Приклад 6.8. Обчислити координати центра ваги півкола, щільність розподілу маси якого пропорційна квадрату відстані точки від діаметра цього півкола.

Рис. 6.16.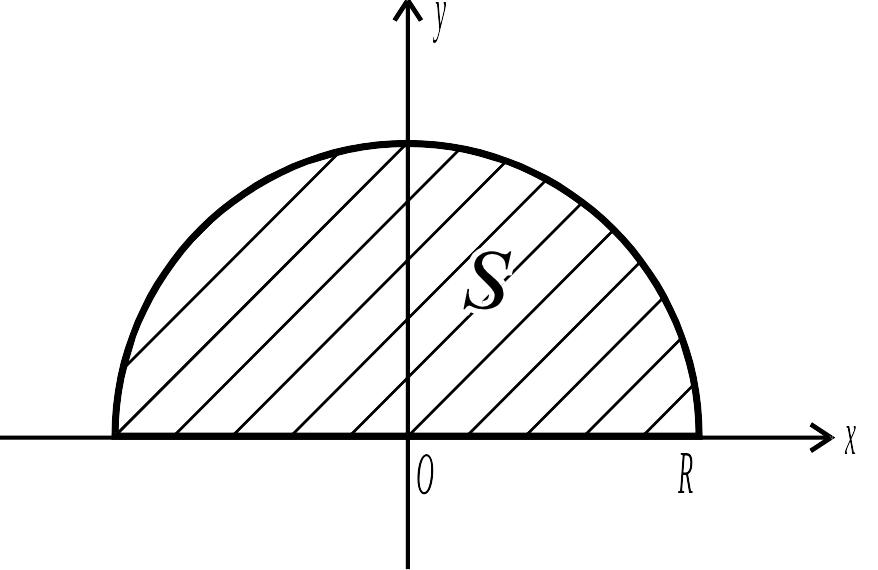

Розв’язання. Нехай вісь проходить через діаметр півкола , а вісь перпендикулярна до вісі у його центрі (рис. 6.16). При такому виборі осей координат щільність ( – коефіцієнт пропорційності), , , де ,

,

, .

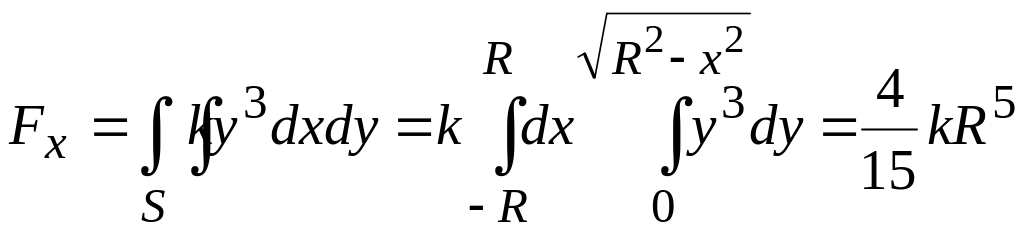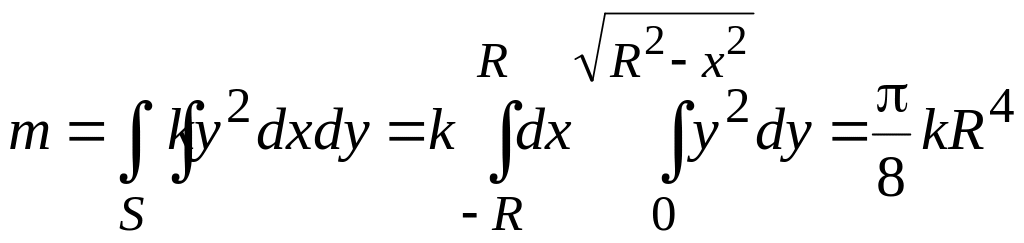7. 7. Поняття про потрійний інтеграл

Нехай у деякій замкнутій області простору задана функція трьох змінних . Розіб'ємо область довільно на областей, що не мають загальних внутрішніх точок. У кожній області візьмемо довільно точку . Значення функції в точці помножимо на об'єм і складемо такі добутки по всіх областях ділення. Отримана сума буде інтегральною сумою функції по області .

Означення 6.1. Потрійним інтегралом функції по області називається границя інтегральної суми цієї функції по області за умови що і ця границя існує, тобто

. (6.17)

Якщо невід’ємна функція – відома щільність розподілу маси тіла, , то маса тіла дорівнює

. (6.18)

Ця рівність є механічним змістом потрійного інтеграла.

Якщо , то

.

Враховуючи, що елемент об'єму у прямокутних координатах обчислюється за формулою , одержуємо формулу для обчислення об'єму тіла V за допомогою потрійного інтеграла:

. (6.19)

Виходячи з означення потрійного інтеграла можна сформулювати його основні властивості.

1) Сталий множник можна виносити за знак потрійного інтеграла, тобто

.

2) Потрійний інтеграл від суми функцій дорівнює сумі потрійних інтегралів від доданків за тією ж областю:

.

3) Якщо область розбита на дві області, які не мають загальних внутрішніх точок, то

.

4) Якщо в області , то

.

5) Якщо в області

, то .

6) Модуль потрійного інтеграла не перевищує потрійного інтеграла модуля функції, що інтегрується, тобто .

Для потрійного інтеграла можна довести теорему про середнє значення.

Теорема 6.3. Якщо функція неперервна в замкнутій області , то в цій області існує така точка , що

,

де – об'єм даної області.

Обчислення потрійних інтегралів відбувається шляхом послідовного обчислення інтегралів меншої кратності.

За аналогією до подвійного інтеграла (рис. 6.17) будемо мати

.

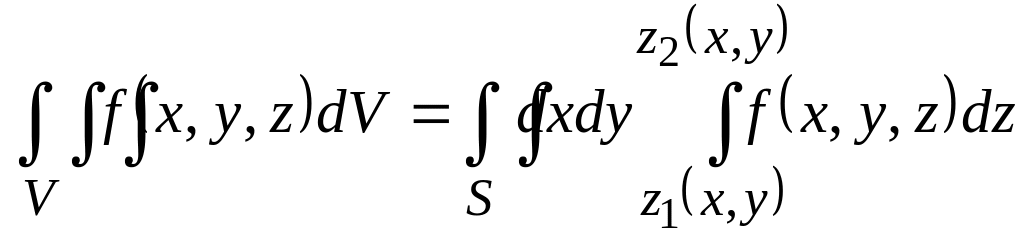Якщо, крім того, проекцією області на площину є область, яка визначається системою нерівностей то

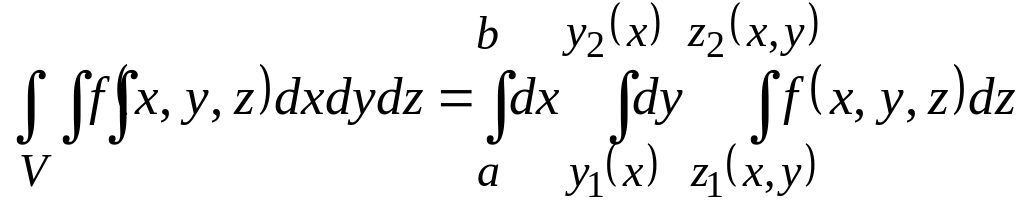. (6.20)

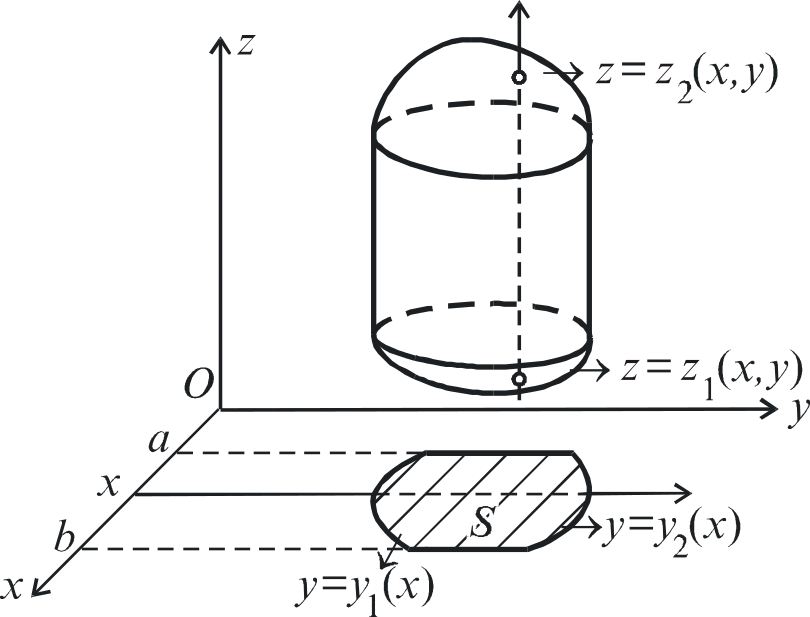
Рис. 6.17.

При обчисленні потрійного інтеграла за формулою (6.20) за допомогою повторного інтеграла спочатку обчислюється внутрішній інтеграл за змінною при сталих і , а потім отримана функція послідовно інтегрується за змінною і, нарешті, за змінною .

Зокрема, якщо область – паралелепіпед із гранями то

. (6.21)

Приклад 6.9. Обчислити інтеграл по області, що обмежена площинами , , , (рис. 6.18).

Рис. 6.18.

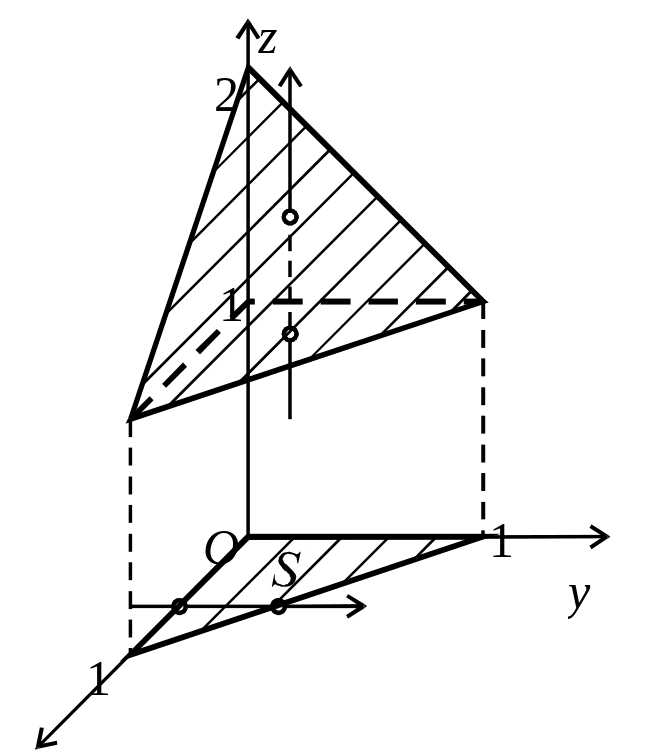
Розв’язання. Область проектується на площину в область, обмежену прямими , , , яку можна записати за допомогою системи нерівностей

Одержуємо