106. 18. Властивості функцій, неперервних в точці

Теорема 2.7. Сума, різниця, добуток скінченного числа функцій, неперервних у точці , також неперервні в цій точці.

Теорема 2.8. Частка від ділення двох функцій, неперервних у деякій точці , також неперервна в цій точці за умови, що знаменник у цій точці не дорівнює нулю.

Теореми доводяться на підставі відповідних теорем про границі.

Доведемо, наприклад, теорему 2.8. Нехай функції і неперервні в точці і . Це значить, що , .

Розглянемо функцію . Для цієї функції:

,

тобто функція неперервна в точці .

Теорема 2.9. Якщо функція неперервна в точці , а функція неперервна в точці , причому , то складна функція неперервна в точці .

Покажемо, що для складної функції виконується означення неперервності: , тобто складна функція неперервна в точці .

На підставі приведених теорем можна стверджувати, що всяка елементарна функція неперервна в кожній точці своєї області визначення.

107. 19. Точки розриву і їхня класифікація

Нехай функція визначена в деякому околі точки . Якщо функція неперервна в точці , для неї виконується означення неперервності. Якщо хоча б одна з рівностей (2.15) порушується, говорять, що функція в точці терпить розрив, а сама точка називається точкою розриву.

Якщо односторонні границі функції в точці рівні, але не дорівнюють значенню функції в точці, тобто , говорять, що в точці усувний розрив. Прикладом такого розриву є розрив функції в точці . Дійсно, функція визначена, а значить і неперервна для всіх , крім . У самій точці функція не визначена, але , отже, маємо усувний розрив. Досить довизначити функцію в точці , поклавши . Нова функція

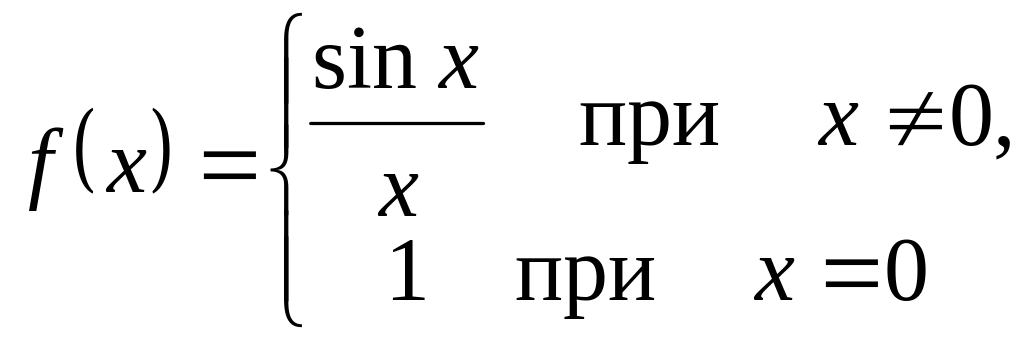
неперервна в точці і на всій числовій прямій.

Якщо односторонні границі функції в точці різні, але обидві скінченні, то говорять, що в цій точці розрив першого роду. Наприклад, функція не визначена в точці .

Обчислимо односторонні границі функції в зазначеній точці, використовуючи символічні записи:

, .

Отже, в точці функція терпить розрив першого роду. Графік такої функції зображений на рис. 2.32.

Розрив першого роду називають розривом зі скінченним стрибком.

Якщо ж хоча б одна з однобічних границь функції в точці дорівнює нескінченності, говорять, що в точці розрив другого роду або розрив з нескінченним стрибком.

Такий розрив має функція в точці .Дійсно:

;

Графік функції зображений на рис. 2.33.

Рис. 2.32.	Рис. 2.33.

Приклад 2.13. Дослідити на неперервність функцію:

Рис. 2.34.

Розв’язання. Оскільки всі елементарні функції неперервні в кожній точці своєї області визначення, функції і неперервні на всій числовій прямій. Досліджуємо точку . Обчислимо односторонні границі функції в точці:

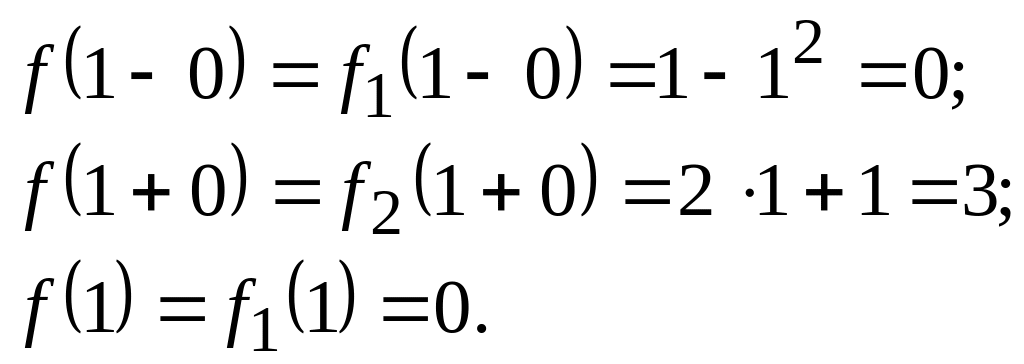
Отже, задана в умові функція неперервна в кожній точці числової прямої, крім точки . У точці функція терпить розрив першого роду. Графік функції зображений на рис. 2.34.