97. 9. Основні методи побудови графіків функцій

Нехай графік функції відомий.

Графік функції зображає собою початковий графік, паралельно перенесений вздовж вісі абсцис на величину, рівну , тобто при – вправо, при – вліво.

Графік функції одержимо паралельним перенесенням графіка вздовж вісі на одиниць вверх при і на одиниць вниз при .

Рис. 2.17.

Так, графік функції побудуємо, змістивши графік функції на одну одиницю вліво і на три одиниці вниз. Для спрощення побудови можна зобразити графік початкової функції в новій системі координат , потім змістити вісь ординат на одиницю вправо і вісь абсцис на три одиниці вверх. Графік функції зображено на рис. 2.17.

Для побудови графіка функції потрібно графік функції деформувати в разів вздовж вісі , тобто “стиснути” при і “розтягти” при .

Неважко помітити, що при від'ємному значенні графік отриманої при деформуванні функції додатково дзеркально відображається відносно вісі абсцис.

Графік функції при додатному значенні одержимо з графіка деформуючи його в разів вздовж вісі абсцис, тобто “стискаючи” при і “розтягуючи” при . При отриманий внаслідок деформації графік додатково дзеркально відображається відносно вісі ординат. На рис. 2.18 зображено графік функції .

При побудові графіка потрібно враховувати його симетрію і періодичність.

Варто пам'ятати, що графік парної функції симетричний щодо вісі , тому досить побудувати лише праву половину графіка і дзеркально відобразити її відносно вісі ординат.

SHAPE \* MERGEFORMAT

Рис. 2.18.

Графік непарної функції симетричний відносно початку системи координат, тому, аналогічно попередньому, досить побудувати частину графіка для і відобразити її симетрично відносно точки .

Для побудови графіка періодичної функції досить зобразити його на відрізку, довжина якого дорівнює періоду і потім циклічно продовжити по всій області визначення, прийнявши однаковими значення ординат точок, абсциси яких розрізняються на число, кратне періоду.

Для побудови графіка функції , за умови, що графіки функцій і відомі, можна скористатися додаванням графіків, що виконується таким способом: для одного значення з області визначення функції відповідне значення одержуємо додаванням спрямованих відрізків, рівних значенням і . Узявши різні значення , побудуємо кілька точок, що належать графіку суми .

На рис. 2.19 зображено графік функції .

Рис. 2.19.

Знаючи графік функції , неважко побудувати графік функції . У точках, де , функція не визначена. Проміжки знакопостійності цих функцій збігаються, значення обернені за величиною. На проміжках, де значення функції зменшуються, значення функції збільшуються, і навпаки.

На рис. 2.20 зображено графік функції .

Рис. 2.20.

98. 10. Приклади застосування функцій в економіці

Функції находять широке застосування в економічній теорії та практиці. Це можуть бути як найпростіші лінійні функції так і складні, що задаються рекурентними співвідношеннями. Розглянемо основні функції.

1. Функція корисності. Це залежність користі деякої дії від рівня , тобто інтенсивності цієї дії. Графік цієї функції зображено на рис. 2.21.

2. Виробнича функція. Це залежність результату виробничої діяльності від обумовлюючих її факторів.

3. Функція випуску (частинний випадок виробничої функції). Це залежність об’єму виробництва від наявності або споживання ресурсу . Графік функції зображено на рис. 2.22.

4. Функція витрат (частинний випадок виробничої функції). Це залежність витрат виробництва від об’єму продукції . Графік функції зображено на рис. 2.23.

5. Функція попиту, споживання та пропозиції. Це залежність об’єму попиту, споживання чи пропозиції на окремі товари та послуги від різних факторів, наприклад, ціни, прибутку тощо.

Графіки функцій попиту та пропозиції від ціни зображено на рис. 2.24 а, б.

Всі ці функції достатньо складно виразити аналітично. При необхідності їх знаходять методами аналізу або наближають за допомогою елементарних функцій.

6. Функція податкової ставки. Це залежність податкової ставки в % від величини річного прибутку . Ця функція відома усьому суспільству і законодавчо затверджена.

Наведемо приклади застосування деяких функцій.

Функції Торнквіста. Досліджуючи залежності попиту на різні товари від прибутку, розглянемо функції Торнквіста:

;

;

.

Можемо встановити рівні прибутків , , при яких розпочинається придбання тих чи інших товарів та рівні насиченості , для товарів першої та другої необхідності.

Графіки функції Торнквіста зображено на рис. 2.25.

Функції попиту та пропозиції. Розглянемо в одній системі координат криві попиту та пропозиції (рис. 2.26).

Одержимо рівноважну (ринкову) ціну даного товару в умовах конкурентного ринку.

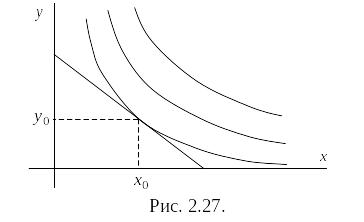
Функції байдужості та функції бюджетного обмеження. Вивчаючи в теорії попиту криві байдужості (лінії, вздовж яких корисність двох благ та одна й та сама), наприклад, які задаються в вигляді та лінію бюджетного обмеження , де – прибуток споживача, а і – ціни благ та відповідно, ми можемо встановити оптимальні кількості благ та , які мають найбільшу корисність.

Графіками кривих байдужності є гіперболи, а графіком функції бюджетного обмеження є пряма лінія (рис. 2.27).