- •1. Випадкові величини і розподіли
- •2. Основні числові характеристики розподілу
- •3. Біноміальний, рівномірний і нормальний розподіли
- •3.1 Біноміальний розподіл ймовірностей
- •3.2 Рівномірний дискретний розподіл
- •3.3 Рівномірний неперервний розподіл
- •3.4 Нормальний розподіл ймовірностей
- •3.5 Нормальне наближення
- •3.6 Розподіли, пов’язані з нормальним
- •1) Розподіл 2 (хі-квадрат)
- •2) Розподіл Стьюдента ( -розподіл)
- •3.7 Оцінки параметрів нормального розподілу
- •Зміст практичного заняття
Практичне заняття № 7
Тема: Визначення ймовірнісних та числових характеристик
випадкових величин
Оцінки параметрів розподілу
Мета заняття: Засвоїти методи визначення ймовірнісних та числових характеристик випадкових величин. Засвоїти методи визначення оцінок параметрів розподілу.
Короткі теоретичні відомості
1. Випадкові величини і розподіли
Нехай
заданий деякий ймовірнісний
простір
 ,
де
,
де
 – простір елементарних подій деякого
випадкового експерименту,
– простір елементарних подій деякого
випадкового експерименту,
![]() –
–
 -алгебра
подій,
-алгебра
подій,
 – ймовірність, тобто числова функція,
визначена на
,
яка задовольняє аксіомам Колмогорова.
– ймовірність, тобто числова функція,
визначена на
,
яка задовольняє аксіомам Колмогорова.
Випадковою
величиною називається
числова функція
 від елементарної події
від елементарної події
 ,
якщо
,
якщо
 подія
подія
 належить
-алгебрі
,
тобто визначена ймовірність
належить
-алгебрі
,
тобто визначена ймовірність
 .
.
Кожній випадковій величині ставиться у відповідність деяка числова множина – множина значень випадкової величини.
Якщо множина значень випадкової величини дискретна, то випадкова величина називається дискретною.
Якщо множина значень випадкової величини неперервна, то випадкова величина називається неперервною.
Законом розподілу випадкової величини називається будь-яке правило, що встановлює зв'язок між можливими значеннями випадкової величини і їхніми ймовірностями.
Закон розподілу є повною характеристикою випадкової величини. Він може мати різні форми: функція розподілу, щільність розподілу, таблиця ймовірностей окремих значень випадкової величини та ін.
Закон
розподілу дискретної випадкової величини
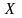 задається
таблицею
задається
таблицею
|
|
|
... |
|
... |
|
|
|
... |
|
... |
при
умові
 (умова нормування).
(умова нормування).
Закон
розподілу неперервної випадкової
величини
задається
за допомогою кусково–неперервної
функції
 –
щільності ймовірності, так, що для
будь-яких
–
щільності ймовірності, так, що для
будь-яких
 справедлива рівність:
справедлива рівність:
 ,
,
при
умові
 (умова нормування).
(умова нормування).
Функцією
розподілу ймовірностей
довільної випадкової величини
![]() називається функція, яка представляє
розподіл величини
:
значення цієї функції в точці
називається функція, яка представляє
розподіл величини
:
значення цієї функції в точці
 дорівнює ймовірності того, що випадкова
величина
набуває значення менше
дорівнює ймовірності того, що випадкова
величина
набуває значення менше
 :
:
 .
.
2. Основні числові характеристики розподілу
Математичне сподівання випадкової величини
 – для
дискретної ВВ,
– для
дискретної ВВ,
 – для
неперервної ВВ.
– для
неперервної ВВ.
Дисперсія
 – означення,
– означення,
 – робоча
формула для обчислення дисперсії.
– робоча
формула для обчислення дисперсії.
Зауваження.
Дисперсія
не може бути від’ємною величиною
 .
.
Середнє квадратичне відхилення
 .
.
3. Біноміальний, рівномірний і нормальний розподіли
Найбільш вживаними в криптологічних застосуваннях є біноміальний, рівномірний і нормальний розподіли.
3.1 Біноміальний розподіл ймовірностей
Дискретна
випадкова величина
 називається розподіленою за біноміальним
законом, якщо її можливими значеннями
називається розподіленою за біноміальним
законом, якщо її можливими значеннями
 є числа успіхів
є числа успіхів
 в схемі Бернуллі при
в схемі Бернуллі при
 випробуваннях, а ймовірності знаходяться
за формулою Бернуллі
випробуваннях, а ймовірності знаходяться
за формулою Бернуллі
 ,
(
,
( ,
,
 ).
).
Закон розподілу:
|
0 |
1 |
... |
|
... |
|
|
|
|
|
... |
|
... |
|
|
Позначається
біноміальний розподіл так:
 ,
де
і
,
де
і
 – параметри біноміального розподілу.
– параметри біноміального розподілу.
Функція розподілу:

Числові характеристики:
 ,
,
 ,
,
 ,
,
 .
.
Найімовірніше
значення
 випадкової величини
,
розподіленої за біноміальним законом
задовольняє нерівність:
випадкової величини
,
розподіленої за біноміальним законом
задовольняє нерівність:
 .
.