
- •Раздел 1. Введение.
- •Раздел 2. Финансовая арифметика.
- •Переменные ставки простых процентов
- •Сложные проценты
- •Сравнительный анализ простых и сложных процентов
- •Раздел 3. Номинальные ставки
- •Переменные ставки сложных процентов.
- •Финансовая рента
- •Сложная или -рента
- •Анализ инвестиций
- •Оптимальное множество парето
- •Выбор наилучшей финансовой операции в условиях полной неопределённости
- •Выбор наилучшей финансовой операции в условиях частичной определённости
- •Диверсификация рисков
ФИНАНСОВАЯ МАТЕМАТИКА Дмитриев Николай Пименович |
30.01.2012 Лекция |
Курс: 6 лекций и 7 семинаров.
Наука в образовательные программы введена недавно, однако изучалась ещё в царской Руси, где российские студенты достигали значительных успехов.
Литература:
Батракова Л. Г. – “Финансовые расчёты в коммерческих сделках”
Башарин Г. П. – “Начала финансовой математики”
Жуленев С. В. – “Финансовая математика. Введение в классическую теорию”. Издательство: МГУ
Малыхин В. И. – “Финансовая математика”
Медведев Г. А. – “Начальный курс финансовой математики”
Капитоненко В. В. – “Финансовая математика и её приложения” (упор больше на страховую математику)
Кутуков В. В. – “Основы финансовой и страховой математики”
Четыркин В. М. – “Методы финансовых и коммерческих расчётов” (одна из первых книг в России о предмете)
Чуйко А. С., Шершнёв В. Г. – “Математические основы финансового обслуживания”
Ширяев А. Н. – “Основы стохастической математики” (в двух томах)
Все процессы в финансах происходят совершенно случайно, что обуславливает большую роль теории вероятностей в финансовой математике.
Основные разделы курса:
Введение
Финансовая арифметика
Номинальные ставки
Финансовая рента
Анализ инвестиций
Вероятностные схемы (приложение)
Также существует такая наука как актуарная математика. Актуарии – это люди, занимающиеся страхованием.
Раздел 1. Введение.
Впервые финансовыми расчётами начали заниматься англичане (XVII – XVIII века). Ими занимались математики, физики и даже астрономы, словом, далёкие от финансов люди. Затем появились специалисты. Примерно в XVIII веке финансисты наткнулись на неразрешимые задачи. Например, требовалось найти корни алгебраических уравнений 7-й и 8-й степени с переменными коэффициентами. Поэтому XIX и XX век были веками провала финансовых расчётов, пока не появились ЭВМ – сначала на западе, а потом и у нас.
Рассмотрим простейшую кредитную операцию с участием всего лишь двух сторон: одна сторона – инвестор (даёт деньги), а вторая – заёмщик (берёт деньги).
 – начало финансовой операции,
– начало финансовой операции,
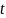 – окончание финансовой операции,
– окончание финансовой операции,
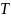 – продолжительность финансовой операции,
– продолжительность финансовой операции,
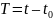
 – начальная денежная стоимость
– начальная денежная стоимость
 – конечная денежная стоимость
– конечная денежная стоимость
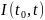 – абсолютное приращение капитала
– абсолютное приращение капитала
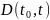 – дисконт (скидка)
– дисконт (скидка)
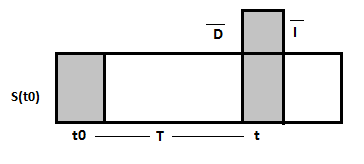
< , т.е. деньги всегда возвращаются в большем объёме, а вот на сколько больше – это и есть денежное приращение.
 (0.1)
(0.1)
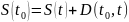 (0.2)
(0.2)
Т.е. численно приращение от дисконта ничем не отличается, однако используется в разных финансовых операциях.
Формула (0.1) выражает финансовую операцию наращение денег. Формула (0.2) выражает операцию дисконтирования (или учёта) денег. Формулы (0.1) и (0.2) являются основными формулами для денежных расчётов. Их недостаток заключается в том, что они выражают деньги, а с миллионами-миллиардами их использование становится неудобным.
Процентной ставкой называется отношение приращение капитала к начальной денежной сумме.
Формула процентной ставки:
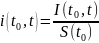 (0.3)
(0.3)
Учётной ставкой называется отношение дисконта к конченой денежной сумме.
Формула учётной ставки:
 (0.4)
(0.4)
Перепишем формулы (0.1) и (0.2) через эти ставки:
 (0.5)
(0.5)
 (0.6)
(0.6)
Эти формулы выражают безразмерную величину, поэтому их использование намного удобнее.
Коэффициентов
наращение называется величина
 ,
по-другому его называют множителем
наращения или мультиплицирующим
множителем.
,
по-другому его называют множителем
наращения или мультиплицирующим
множителем.
Коэффициентом
дисконтирования называется величина
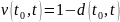 .
.
Перепишем формулы (0.1) и (0.2) через эти коэффициенты:
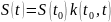 (0.7)
(0.7)
 (0.6)
(0.6)
Основными базовыми периодами начисления или учёта денег считаются: год, полгода, квартал, месяц, неделя, день, час, минута, секунда. И самый маленький промежуток – мгновение. Это бесконечно малая, предел равен 0. Даже на таком периоде как мгновение происходит наращение денег. Но здесь уже нужно интегрировать.
Самым основным периодами является финансовый год. Длительность операции на данном периоде принимают за единицу.
Приращение является инвариантным, т.е. не имеет привязки по времени.

Если базовым промежутком является год, то приняты следующие сокращения:
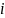 – годовая процентная ставка,
– годовая процентная ставка,
 – Годовая учётная ставка,
– Годовая учётная ставка,
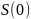 – начальная денежная сумма,
– начальная денежная сумма,
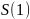 – конечная денежная сумма через год.
– конечная денежная сумма через год.
С учётом этих сокращений формулы примут следующий вид:
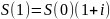 (0.9)
(0.9)
 (0.10)
(0.10)
Эти формулы можно записать и так:
 ,
где k – годовой коэффициент
наращения
,
где k – годовой коэффициент
наращения
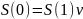 ,
где v – годовой коэффициент
дисконтирования.
,
где v – годовой коэффициент
дисконтирования.
Таким
образом, годовые коэффициенты наращения
и дисконтирования –
 и
и
 – взаимообратным, если начальная и
конечная денежная сумма неизменны:
– взаимообратным, если начальная и
конечная денежная сумма неизменны:
 (0.11).
(0.11).
Ставки, соответствующие равенству (0.11) называются эквивалентными.
Найдём эти ставки:
 (0.12)
(0.12)
Выражения
годовой процентной ставки через
эквивалентную ей годовую учётную ставку:
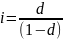 (0.12). Выражение годовой учётной ставки
через эквивалентную ей годовую процентную
ставку:
(0.12). Выражение годовой учётной ставки
через эквивалентную ей годовую процентную
ставку:
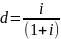 (0.13).
(0.13).
Пусть
учётная ставка
 ,
т.е.
,
т.е.
 .
Тогда соответствующая ей годовая
процентная ставка равна
.
Тогда соответствующая ей годовая
процентная ставка равна
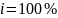 .
Т.е. положим
.
Т.е. положим
 рублей под
рублей под
 в банк, получим через год
в банк, получим через год
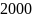 .
.
Пусть
процентная ставка
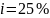 ,
т.е.
,
т.е.
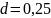 .
Тогда соответствующая ей годовая учётная
ставка равна
.
Тогда соответствующая ей годовая учётная
ставка равна
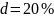 .
.
Пусть
учётная ставка
 ,
т.е.
,
т.е.
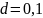 .
Тогда соответствующая ей годовая
процентная ставка равна
.
Тогда соответствующая ей годовая
процентная ставка равна
 .
.
По
нашим примерам получается, что
 .
.
Это соотношение всегда верно.
