Тема «Математико-статистические основы выборочного метода».

Числовые характеристики генеральной совокупности, как правило, - неизвестные, (средняя, дисперсия и др.) называются параметрами (характеристиками) генеральной совокупности (обозначаются, например, или , ). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р.

По выборочным данным рассчитывают числовые характеристики, которые называют выборочными характеристиками (статистиками) (обозначаются , или , , выборочная доля обозначается w).

Если из генеральной совокупности объема N извлекается выборка объема n, причем значение признака х₁ наблюдается m₁ раз, х₂ - m₂ раз,..., х_k - наблюдается m_k раз, то - объем выборки.

Вместо частот m_i каждому значению x_i можно сопоставить относительную частоту (частость) w_i=m_i/n.

Определенным образом заданное соответствие между возможными значениями признака x_i и соответствующими им весами (частотами - m_i или относительными частотами (частостями) - w_i) называют статистическим распределением выборки.

Числовые характеристики, получаемые по различным выборкам, как правило, отличаются не только друг от друга, но и от соответствующей характеристики генеральной совокупности. Поэтому числовая характеристика, полученная по выборочным данным, является только статистической оценкой неизвестного параметра генеральной совокупности.

Обозначим Θ неизвестный параметр генеральной совокупности, Θ^* - его статистическую оценку, полученную по выборочным данным.

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Это – требования:

- несмещенности,

- эффективности и

- состоятельности.

Несмещенной называют статистическую оценку Θ^*, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т.е.

M(Θ^*) = Θ.

Смещенной называют статистическую оценку Θ^*, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.

Состоятельной называют статистическую оценку, которая при n → ∞ стремится к оцениваемому параметру, т.е.

.

Различают точечные и интервальные оценки.

Точечной называют оценку, которая определяется одним числом.

В качестве точечных оценок параметров генеральной совокупности используются соответствующие выборочные характеристики. Теоретическое обоснование возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чисел и центральная предельная теорема Ляпунова.

Выборочная средняя является точечной несмещенной, состоятельной, а при известном σ – и состоятельной оценкой генеральной средней, т.е.

_≈

Генеральная дисперсия имеет 2 точечные оценки:

- выборочная дисперсия – смещенная оценка генеральной дисперсии;

- исправленная выборочная дисперсия - несмещенная оценка генеральной дисперсии.

исчисляется при , а - при .

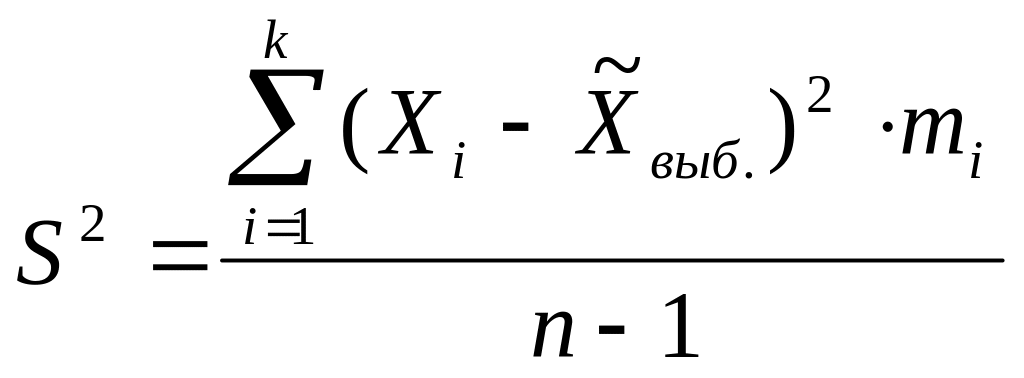
или

При больших объемах выборки и практически совпадают.

Генеральное среднее квадратическое отклонение также имеет 2 точечные оценки:

- выборочное среднее квадратическое отклонение и

- исправленное выборочное среднее квадратическое отклонение.

используется для оценивания при , а для оценивания , при _.

При этом: , а .

Интервальной оценкой называют оценку, которая определяется двумя числами - границами интервала, который с заданной надежностью накрывает неизвестный параметр генеральной совокупности.

Интервал, содержащий оцениваемый параметр генеральной совокупности, называют доверительным интервалом.

Для его определения вычисляется предельная ошибка выборки , позволяющая установить предельные границы, в которых с заданной вероятностью (надёжностью) должен находиться неизвестный оцениваемый параметр генеральной совокупности.

Ошибка репрезентативности может быть представлена как разность между генеральными и выборочными характеристиками изучаемой совокупности:

ε = Θ - Θ^*.

Поскольку оцениваются, как правило, средние или доли, то:

, либо .

Пусть представляет собой предел, которым ограничена сверху абсолютная величина . Тогда: . Следовательно,

.

Мы получили интервальную оценку неизвестного параметра генеральной совокупности.

Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между характеристиками выборочной и генеральной совокупностей будет сколь угодно мала.

,

где t – кратность ошибки,

μ – стандартная (средняя) ошибка выборки,

- предельная ошибка выборки.

Согласно центральной предельной теореме Ляпунова выборочные распределения статистик (при n ³ 30) будут иметь нормальное распределение независимо от того, какое распределение имеет генеральная совокупность. Следовательно:

,

где 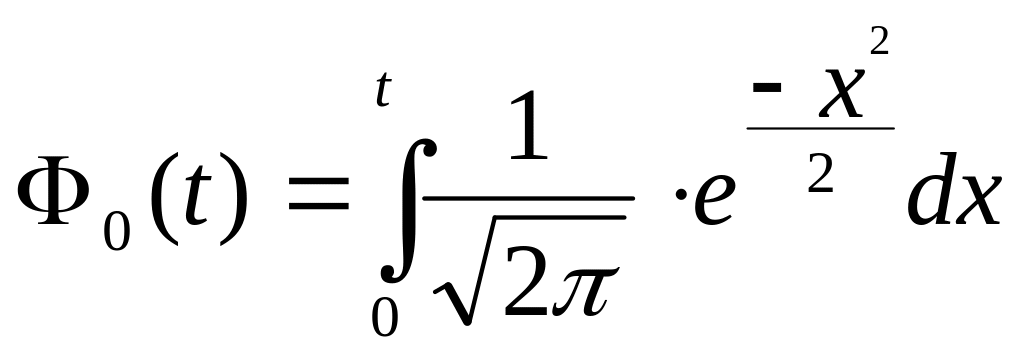- функция Лапласа,

γ – доверительная вероятность (надежность).

Запись показывает, что о величине расхождения между неизвестным параметром генеральной совокупности и его выборочной характеристикой , можно судить лишь с определенной вероятностью, от которой зависит величина t.

Здесь устанавливается связь между пределом ошибки , гарантируемым с некоторой надежностью γ, кратностью ошибки t и стандартной (средней) ошибкой выборки μ.

Надежность γ устанавливается до проведения выборочного обследования. Если γ=0,95, то: со статистической надежностью в 95% доверительный интервал содержит неизвестный оцениваемый параметр генеральной совокупности. Статистической надежности в 95% соответствует доверительная вероятность - 0,95. В 5% случаев утверждение «неизвестный оцениваемый параметр генеральной совокупности принадлежит доверительному интервалу» будет неверным. Т.е. 5% задает уровень значимости ( =0,05) или 0,05 - вероятность ошибки. Доверительная вероятность и уровень значимости дополняют друг друга до 1, т.е. представляют собой сумму вероятностей противоположных событий:

γ+α=1.

При n < 30 выборочные распределения статистик будут иметь распределение Стьюдента. Тогда:

,

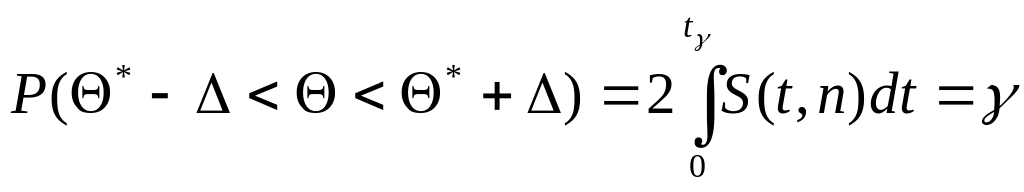где - плотность распределения Стьюдента,

и

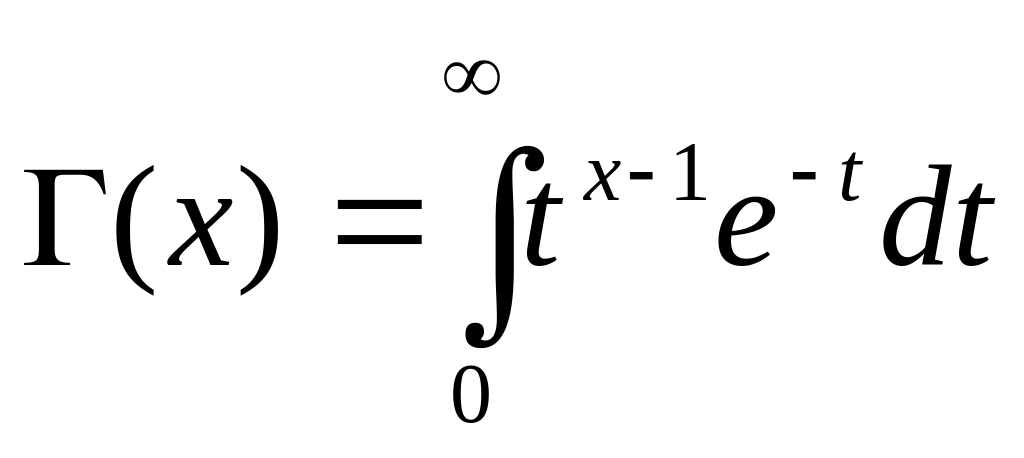- гамма-функция.

Значения вероятностей, соответствующие различным t, содержатся в специальных таблицах: при n ³ 30 - в таблице значений Ф₀(t), а при n < 30 в таблице распределения t-Стьюдента.

При больших выборках, т.е. n ³ 30 t определяется по таблицам функции Лапласа из соотношения 2F₀(t) = g.

При малых выборках, т.е. n < 30 t определяется по таблицам Стьюдента

по уровню значимости a = 1 - g

и числу степеней свободы k = n - 1;

Стандартная (средняя) ошибка выборки μ представляет собой среднее квадратическое (стандартное) отклонение оценки неизвестного параметра генеральной совокупности σ(Θ^*). В зависимости от оцениваемого параметра и способа отбора стандартная (средняя) ошибка выборки μ определяется по различным формулам.

С помощью доверительного интервала можно оценить генеральную среднюю, генеральную долю и другие неизвестные параметры генеральной совокупности.

Границы доверительного интервала генеральной средней при больших выборках можно оценить с помощью следующего соотношения:

,

- при малых:

.

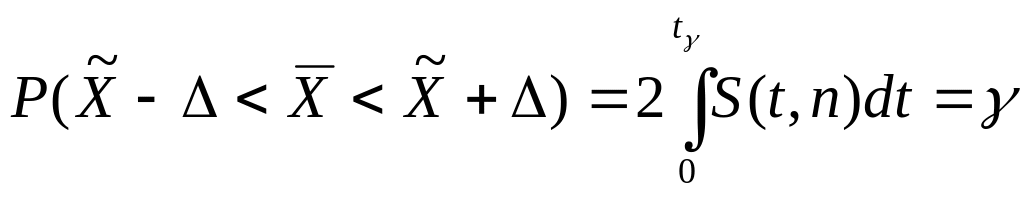Границы доверительного интервала генеральной доли при больших выборках можно оценить с помощью следующего соотношения:

.

При малых:

.

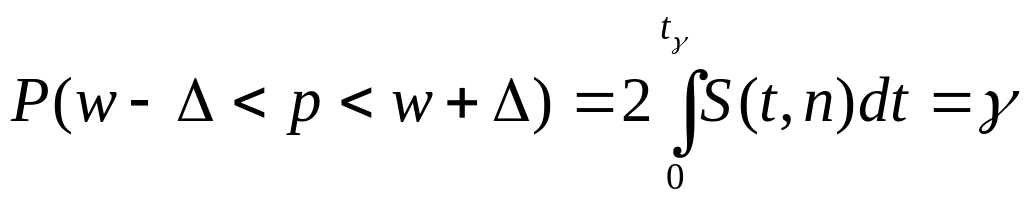Одной из важнейших проблем выборочного метода является определение необходимого объема выборки. От объема выборки зависят надежность оценок параметров генеральной совокупности, размеры стандартной (средней) μ, а, значит, и предельной Δ ошибок выборки и экономичность проводимого выборочного наблюдения, т.к. чем больше объем выборки, тем больше затраты на изучение элементов выборки, но тем меньше при этом ошибки выборки.

Расчет минимально необходимой численности выборки – это ответ на вопрос: «Сколько нужно обследовать единиц генеральной совокупности, чтобы с заранее заданной надежностью γ не превысить заранее заданную ошибку Δ?». Необходимо помнить, что точность и надежность оценок необходимо задавать до проведения выборки.

Формулы расчета необходимой численности выборки n для различных способов отбора можно получить из формул предельной ошибки и, соответственно, формул стандартных (средних) ошибок выборки.