10. Розклад многочлена на множники

Із вищої алгебри відомо, що алгебраїчне рівняння степеня має коренів — дійсних чи комплексних, простих чи кратних. Многочлен степеня

можна представити у вигляді добутків двучленів , де — корінь рівняння

,

тобто у вигляді

. (26)

Представлення многочлена у вигляді (26) називають розкладом многочлена на множники.

Приклад . Розкласти на множники многочлен

Розв’язання. Позначимо . Тоді заданий многочлен набуває вигляду . Розв’язуємо рівняння . Корені цього рівняння . Тоді

.

Оскільки , то і потрібно знайти корені степеня із комплексних чисел .

Запишемо число в тригонометричній формі: . Маємо . Для знаходження використаємо формули (25). Маємо , . Тоді

Комплексне число відрізняється від комплексного числа тільки модулем: Тоді . Використовуючи формули (25) та враховуючи знайдені корені , дістаємо корені із комплексного числа :

Таким чином, маємо розклад заданого многочлена на множники:

.

11. Показникова форма комплексного числа

Наведемо (без доведення) деякі відомості із математичного аналізу, які потрібні для введення показникової форми комплексного числа.

Означення. Числовою послідовністю називають функцію , аргументом якої є натуральне число .

Позначають послідовність так: , або , або .

При цьому називається загальним членом послідовності. Якщо відомий загальний член послідовності, то можна записати будь-який член цієї послідовності.

Дамо означення границі числової послідовності дійсних чисел.

Означення. Число називається границею числової послідовності , якщо для будь-якого, наперед заданого, достатньо малого, додатного числа існує такий номер , який залежить від , що для всіх виконується нерівність

.

Позначають границю так: .

Розглянемо числову послідовність

. (27)

Запишемо декілька членів цієї послідовності:

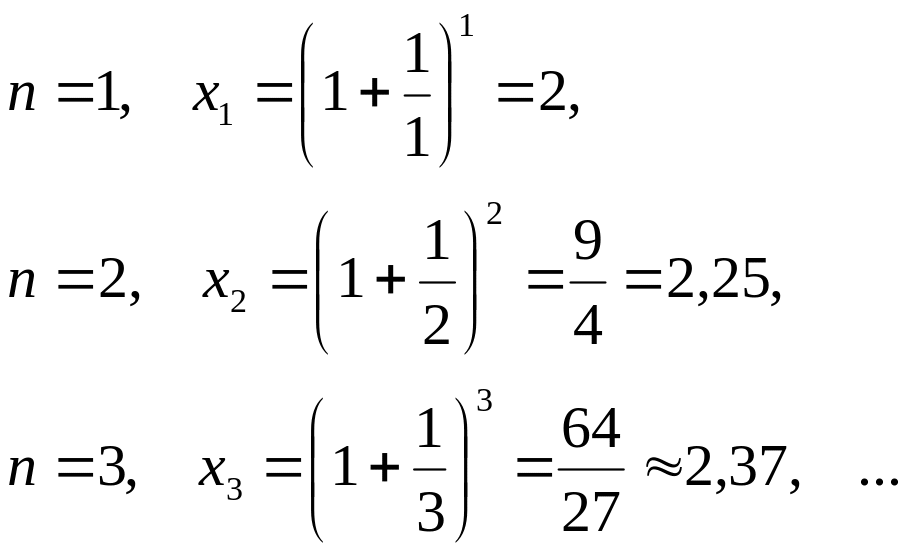
Послідовність , має границю. Ця границя — число Ейлера , тобто

.

Можна довести, що границя послідовності є функція

. (28)

Розглянемо послідовність комплексних чисел

де

Означення. Число називається границею послідовності комплексних чисел , якщо для будь-якого, наперед заданого, достатньо малого, додатного числа існує такий номер , який залежить від , що для всіх виконується нерівність

.

Позначають границю так: .

Нехай існують границі послідовностей дійсної і уявної частини комплексних чисел: Враховуючи, що , маємо

.

Границя послідовності комплексних чисел існує тоді і тільки тоді, коли існують границі послідовностей дійсних чисел .

Означення. Функцією комплексної змінної називається правило, за яким кожному комплексному значенню із деякої області комплексної площини ставиться у відповідність одне або декілька значень із області іншої комплексної площини.

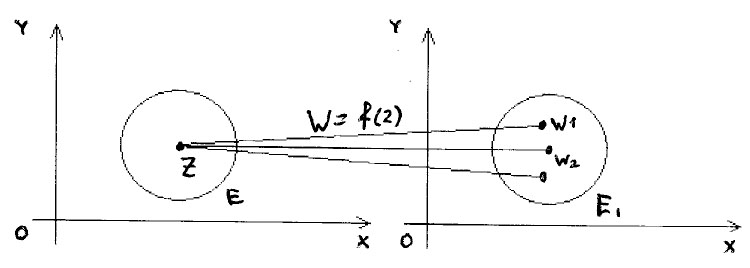
Рис. 12

Позначається комплексна функція так .

Одну із комплексних функцій ми розглянули, коли виконували операцію добування кореня із комплексного числа: . При цьому одному значенню комплексної змінної , було поставлено у відповідність значень функції : , .

Функцію комплексної змінної визначимо аналогічно тому, як визначали функцію дійсної змінної , тобто

.

З іншої сторони, функцію дійсної змінної можна представити у вигляді розвинення в ряд (таке представлення обгрунтовується в розділі вищої математики «Ряди»):

. (29)

Наведемо також розвинення в ряди функцій та

,

.

Аналогічні формули розвинення в ряди мають місце і для функцій комплексної змінної. А саме,

. (30)

Нехай . Тоді, враховуючи ряди для функцій та , маємо

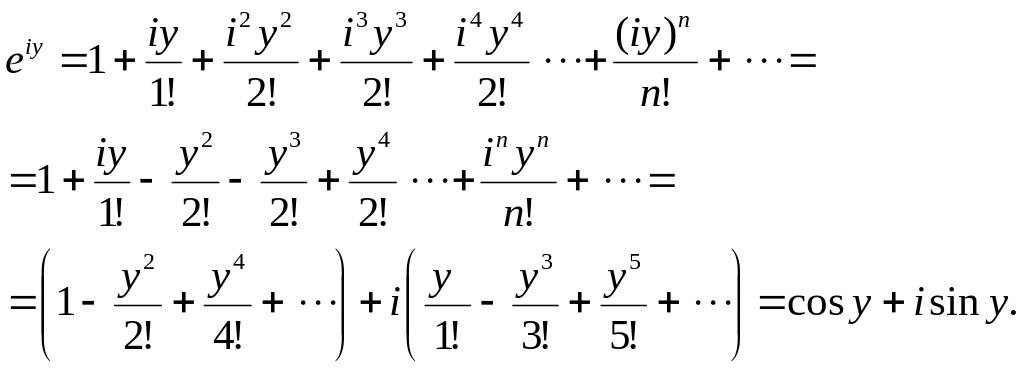
Таким чином,

(31)

Заміняючи на , дістаємо або

(32)

Якщо додати ліві і праві частини рівностей (31) та (32), то дістанемо, що

.

Якщо відняти ліві і праві частини рівностей (31) та (32), то дістанемо, що .

Після заміни на в цих формулах маємо формули Ейлера

, . (33)

Якщо у формулі (31) замінити на , то ця формула набуває вигляду

(34)

Запишемо комплексне число у тригонометричній формі:

. Із формули (34) дістаємо, що , тоді число набуває вигляду .

Представлення комплексного числа у вигляді

. (35)

називається показниковою формою комплексного числа. При цьому .

Властивості функції

Розглянемо показникову функцію , де і наведемо деякі її властивості.

Маємо .

Або

. (36)

Звідки отримуємо, що модуль функції дорівнює , , а аргумент функції дорівнює .

11.1. Для показникової функції мають місце формули

. (37)

Доведемо першу із формул (37). Нехай . Використаємо представлення функції у вигляді (36) і правило множення чисел в тригонометричній формі. Тоді

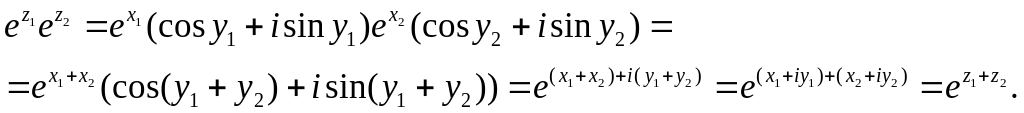
Інші формули (37) доводяться аналогічно. Доведіть їх самостійно.

11.2. Функція є періодичною функцією з суто уявним періодом .

Покажемо це. Використовуємо формулу (37) і показникову форму функції . Маємо , тобто

. (38)

11.3. Періодом функції є також суто уявне число , де — ціле число:

,

Дійсно, .

11.4. Крім функція інших періодів не має.

Нехай — період функції, тобто . Звідки при маємо .

Нехай — комплексне число вигляду . Тоді або , тобто . Звідки і . Тоді . Отже, , а це і означає, що інших переодів, крім немає.

Приклад. Записати число в алгебраїчній, тригонометричній і показниковій формі.

Розв’язання. Використаємо формули (37) і формули Ейлера (33):

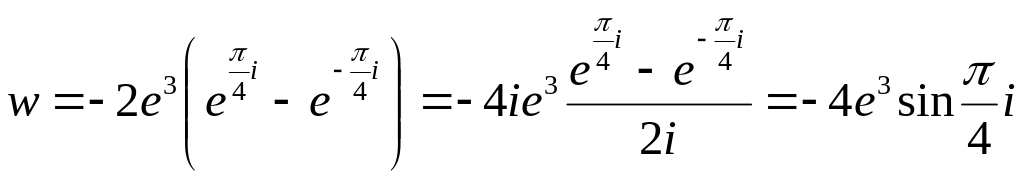. Задане число має вигляд в алгебраїчній формі: .

Враховуючи, що згідно з формулами (13) , маємо задане число в тригонометричній формі . Задане комплексне число має модуль і аргумент . Отже, в показниковій формі .

11.5. Запишемо в показниковій формі дійсні числа та уявні числа , використовуючи їх тригонометричну форму(13). Маємо

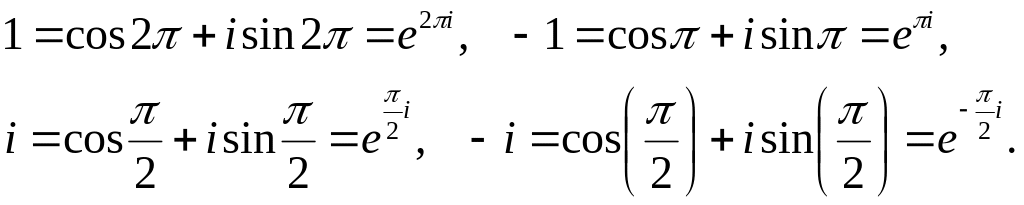
Таким чином, крім формул (13) запису в тригонометричній формі дійсних чисел та уявних чисел маємо запис цих чисел в показниковій формі

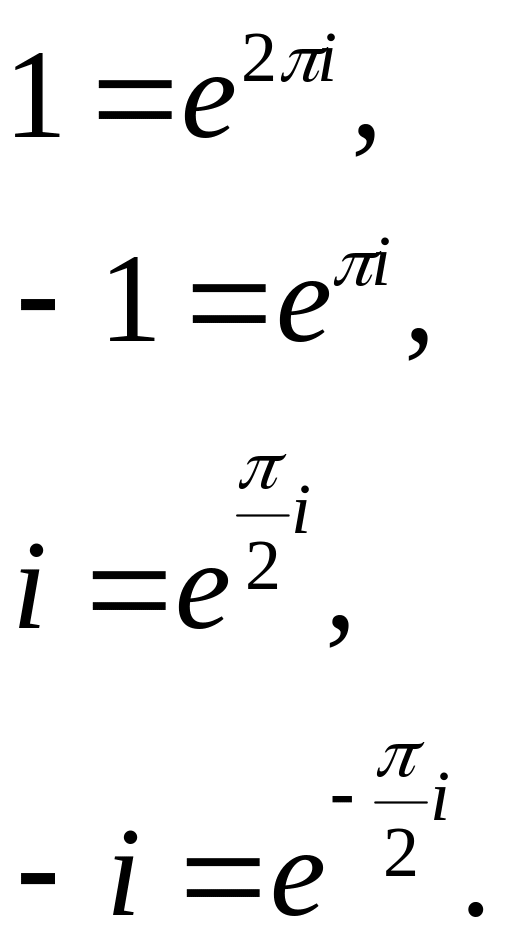(39)

Наведемо ще одну комплексну функцію . Натуральним логарифмом комплексного числа називається комплексне число, що має вигляд

.

Приклад 1. Знайти .

Згідно з означення логарифму комплексного числа маємо .

Приклад 2. Знайти .

Для заданої функції . Знаходимо модуль і аргумент заданого числа. Таким чином, .