
- •Раздел второй кинетика
- •4. Кинетика
- •4.1. Введение в кинетику
- •4.1.1. Предмет кинетики. Основные понятия
- •4.1.2. Основные законы механики
- •4.1.3. Связи и реакции связей
- •4.1.4. Силы трения
- •4.1.5. Классификация связей
- •Вопросы для повторения
- •4.2. Дифференциальные уравнения движения материальной точки
- •4.2.1. Дифференциальные уравнения движения свободной точки
- •4.2.2. Движение несвободной материальной точки
- •4.2.3. Дифференциальные уравнения относительного движения материальной точки
- •4.2.4. Две основные задачи динамики
- •Вопросы для повторения
- •4.3. Введение в динамику механической системы
- •4.3.1. Дифференциальные уравнения движения механической системы
- •4.3.2. Силы, действующие на абсолютно твердое тело
- •4.3.3. Распределенные силы. Центр тяжести
- •4.3.4. Момент силы относительно точки и относительно оси
- •4.3.5. Пара сил
- •4.3.6. Главный вектор и главный момент системы сил. Свойства внутренних сил
- •4.3.7. Приведение системы сил к данному центру
- •4.3.8. Масса и центр масс системы материальных точек
- •4.3.9. Моменты инерции
- •4.3.10. Моменты инерции простейших однородных тел
- •Вопросы для повторения
- •4.4. Теоремы об изменении количества движения и о движении центра масс
- •4.4.1. Количество движения материальной точки и системы материальных точек. Элементарный и полный импульсы силы.
- •4.4.2. Теорема об изменении количества движения системы
- •4.4.3. Теорема о движении центра масс
- •4.4.4. Дифференциальные уравнения поступательного движения твердого тела
- •Вопросы для повторения
- •4.5. Теорема об изменении кинетического момента
- •4.5.1. Кинетический момент точки
- •4.5.2. Кинетический момент системы материальных точек
- •4.5.3. Теорема об изменении кинетического момента системы материальных точек
- •4.5.4. Дифференциальное уравнение вращательного движения твердого тела
- •Вопросы для повторения
- •4.6. Теорема об изменении кинетической энергии
- •4.6.1. Кинетическая энергия точки и системы точек
- •4.6.2. Работа силы
- •4.6.3. Работа силы, приложенной к вращающемуся твердому телу
- •4.6.4. Работа внутренних сил
- •4.6.5. Мощность
- •Вопросы для повторения
- •4.6.6. Теорема об изменении кинетической энергии
- •Вопросы для повторения
- •4.6.7.* Потенциальное силовое поле
- •4.6.8.* Потенциальная энергия
- •4.6.9*. Закон сохранения механической энергии
- •Вопросы для повторения
- •5. Статика
- •5.1. Условия равновесия системы сил, приложенных к твердому телу
- •5.2. Теорема Вариньона о моменте равнодействующей
- •5.3. Условия равновесия систем сходящихся и параллельных сил
- •5.4. Условия равновесия плоской системы сил
- •Решив эту систему, получим
- •5.5. Равновесие системы тел. Примеры решения задач
- •Вопросы для повторения
- •5.6.* Принцип возможных перемещений
- •Вопросы для повторения
- •6. Принцип даламбера
- •6.1. Принцип Даламбера для материальной точки
- •6. 2. Принцип Даламбера для системы материальных точек
- •6. 3 *. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
- •6.4*. Общее уравнение динамики
- •Вопросы для повторения
- •Список литературы Основная
- •Дополнительная
- •4.1. Введение в кинетику ………………………………… . ..141
- •4.1.1.Предмет кинетики. Основные понятия………… ……..141
4.3.9. Моменты инерции
Движение механической системы материальных точек зависит не только от массы системы, но и от распределения этой массы. Так, из двух маховиков одинаковой массы (веса) быстрее раскрутится при одинаковых силах маховик меньшего диаметра. Распределение масс в механической системе характеризуется моментами инерции. Различают следующие моменты инерции:
осевые
![]()
полярный JО;
центробежные
![]()
О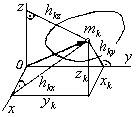 севой
момент инерции равен сумме произведений
массы тk каждой точки
системы на квадрат ее расстояния до
соответствующей оси (рис. 4.38); Полярный
момент инерции равен сумме произведений
массы каждой точки на квадрат ее
севой
момент инерции равен сумме произведений
массы тk каждой точки
системы на квадрат ее расстояния до
соответствующей оси (рис. 4.38); Полярный
момент инерции равен сумме произведений
массы каждой точки на квадрат ее
Рис. 4.38 расстояния до начала координат:
![]() ,
,
![]() ,
(4.60)
,
(4.60)
![]() .
.
Из данных выражений следует, что
![]() .
(4.61)
.
(4.61)
Действительно,
![]()
![]()
![]() +
+
![]()
![]() =2JО.
=2JО.
Центробежный момент инерции равен алгебраической сумме произведений массы каждой точки системы на произведение ее соответствующих координат:
![]() ,
,
![]() .
(4.62)
.
(4.62)
![]() ,
,
Если относительно какой-либо системы координат центробежные моменты равны нулю, то оси этой системы называются главными осями инерции в начале координат. Если же начало этой системы координат совпадает с центром масс, то такие оси называются главными, центральными осями инерции. Главными осями являются: 1) ось материальной симметрии системы материальных точек, 2) ось, перпендикулярная плоскости материальной симметрии системы материальных точек и имеющая начало в плоскости симметрии.
Момент инерции твердого тела относительно заданной оси, например оси Oz, можно представить в виде произведения массы тела на квадрат линейной величины, называемой радиусом инерции тела относительно этой оси:
![]() ,
(4.63)
,
(4.63)
где М — масса тела, ρz — радиус инерции тела относительно оси Оz.
Данная формула показывает, что радиус инерции ρz определяет расстояние от оси Oz до материальной точки, в которой нужно сосредоточить всю массу М тела, чтобы момент инерции полученной точки относительно данной оси равнялся моменту инерции тела. Моменты инерции измеряются в кг·м2.
Н айдем
зависимость между моментами инерции
тела относительно параллельных осей
z и z',
одна из которых, ось z',
проходит через центр масс С тела
(рис. 4.39). Проведем остальные оси
айдем
зависимость между моментами инерции
тела относительно параллельных осей
z и z',
одна из которых, ось z',
проходит через центр масс С тела
(рис. 4.39). Проведем остальные оси
Рис. 4.39 так, как это показано на рисунке, и обозначим через d расстояние между осями Oz и Cz'. Момент инерции тела относительно оси Сz' равен
![]() ,
,
а относительно оси Oz
![]() .
.
Координаты точки
Мk в системах Oxyz
и Cx'y'z'
связаны соотношениями
![]() ,
,
![]() +
d. Подставим эти
значения в выражение для Jz:
+
d. Подставим эти
значения в выражение для Jz:
=![]() =
=
=![]() .
.
Но
![]() =
=![]() ,
,
![]() ,
,
где
М— масса тела, a
![]() ,
так как начало координат системы Cx'y'z'
находится в центре масс тела. Следовательно,
,
так как начало координат системы Cx'y'z'
находится в центре масс тела. Следовательно,
![]() +
Md2.
(4.64)
+
Md2.
(4.64)
Это уравнение выражает теорему Гюйгенса — Штейнера: момент инерции системы материальных точек относительно какой-либо оси равен ее моменту инерции относительно параллельной оси, проходящей через центр масс системы, плюс произведение массы системы на квадрат расстояния между этими, осями.
Из теоремы следует, что наименьший момент инерции — это момент относительно оси, проходящей через центр масс системы.
