Равновесие тела с учетом трения скольжения

2.1.83. На наклонной плоскости лежит груз. Определить в градусах максимальный угол наклона плоскости к горизонту, при котором груз останется в покое, если коэффициент трения скольжения равен 0,6. (31)

2.1.84. Каким должен быть наименьший вес тела 2 (рис. 251), для того чтобы тело 1 весом 200 Н начало скользить по горизонтальной плоскости, если коэффициент трения скольжения f = 0,2. (40,0)

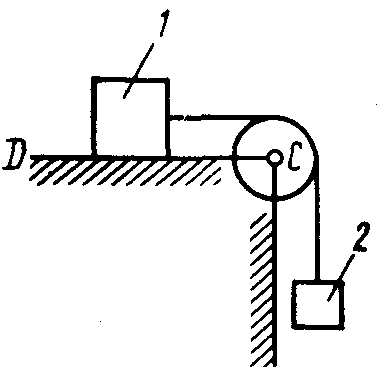
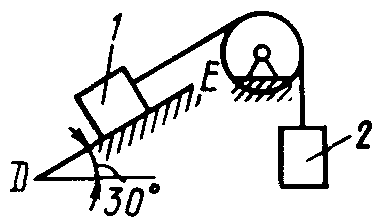
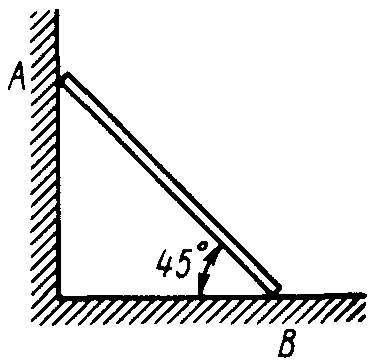
Рис. 251 Рис. 252 Рис.253

2.1.85. Определить наименьший вес тела 1, при котором оно скользит вниз по плоскости DE (рис. 252), если вес груза 2 равен 320 Н, коэффициент трения сколь-жения между телом 1 и плос­костью DE равен 0,2. (979)

2.1.86. Однородный брус АВ (рис. 253) опирается в точке А на гладкую стену, а в точке В на негладкий пол. Определить наименьший коэффициент трения скольжения между брусом и полом, при котором брус останется в указанном поло­жении в покое. (0,50)

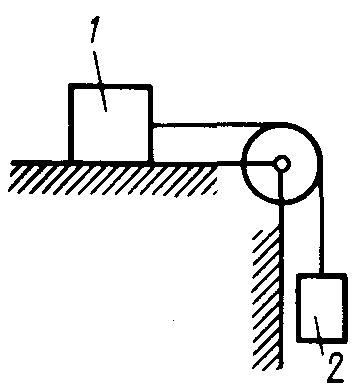
2.1.87. Определить наименьший коэффициент тре­ния скольжения между грузом 1 весом 400 Н и плоскостью DC (рис. 254), при котором груз 1 оста­нется в покое, если вес груза 2 равен 96 Н. (0,24)

2.1.88. Определить наименьший вес груза 1(рис. 255), при котором он останется в покое, если вес груза 2 равен 140 Н, а коэффициент трения скольже­ния между грузом 1 и плоскостью равен 0,2. (700)

2.1.89. Каким должен быть вес тела 1(рис. 256), для того чтобы началось скольжение вверх по наклон­ной плоскости, если сила F = 90 Н, а коэффи­циент трения скольжения f = 0,3? (118)

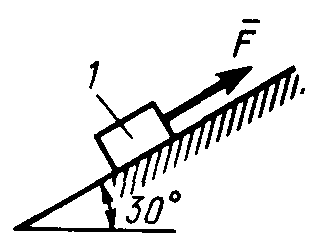
Рис. 254 Рис. 255 Рис. 256

2 .1.90. Каким должен быть наибольший вес груза 2 (рис. 257), для того чтобы груз 1 весом 100 Н оставал­ся в покое на наклонной

Рис. 257 плоскости, если коэффициент трения скольжения f = 0,3? (76,0)

Равновесие тела с учетом трения качения

2.1.91*. Определить модуль горизонталь­ной силы , под действием которой тележка весом G движется равномерно по рельсовому пути (рис. 258), если веса всех колес равны Q, их ра­диусы R, а коэффициент трения качения колес о рельсы равен k. Принять АО=ОВ.

Ответ:

2.1.92*. Катушка радиусом R и весом Р находится в равновесии на горизонтальной плоскости (рис. 259). На среднюю цилиндрическую часть катушки радиусом r намотана нить, переброшенная через идеальный блок А и несущая на своем конце груз D весом Q. Участок нити АВ составляет с вертикалью угол α. Определить момент сил трения качения и реакцию плоскости в точке каса­ния С.

О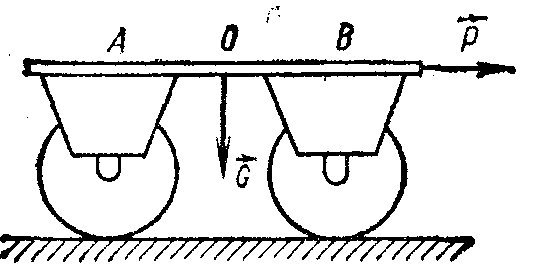 твет: M = Q(R sinα - r) (при М > 0 пара трения качения стремится вращать катушку против хода часовой стрелки); Х_С = - Qsin α; Y_С = Р - Q cos α.

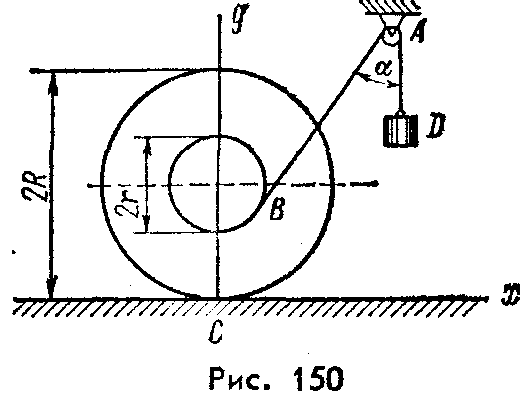
Рис. 258 Рис. 259

2.1.93. Цилиндр весом 520 Н лежит на горизон-тальной плоскости. Опре­делить наименьший модуль момента пары сил, необходимый для качения цилиндра. Коэффициент трения качения δ = 0,007 м. (3,64)

2.1.94. К однородному катку (рис. 260) весом 700 Н прило­жена сила . Определить наименьший модуль этой силы, для того чтобы каток начал ка­титься со скольжением, если радиус R = 1 м, коэффициенты трения скольжения и качения соответственно равны: f = 0,2, δ = 0,008 м. (183)

2.1.95. На однородный каток (рис. 261) весом 2 кН дейст­вуют горизонтальная сила F₂ = 10 Н и верти­кальная сила F₁. Каким должен быть наиболь­ший модуль силы F₁, для того чтобы началось качение катка, если коэффициент трения ка­чения δ = 0,005 м, радиус R = 0,8 м, размер А = 0,4 м? (400)

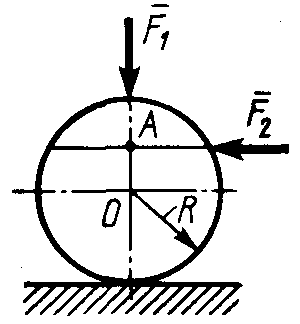
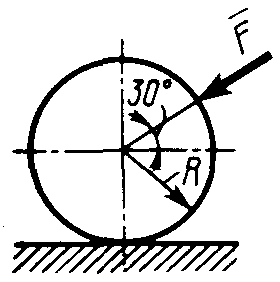
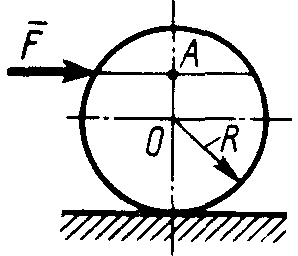
Рис. 260 Рис. 261 Рис. 262

2.1.96. К однородному катку (рис. 262) весом 2 кН прило­жена горизонтальная сила F. Определить наи­больший модуль силы F, при котором каток не скользит и не катится, если коэффициент трения качения δ = 0,006 м, коэффициент трения скольжения f = 0,2, радиус R = 0,6 м, размер ОА = 0,4м. (12,0)

2.1.97. К катку 1 (рис. 263) с помощью нерастяжимой нити подвешен груз 2. Определить наибольший вес этого груза, при котором каток 1 весом 3,2 кН останется в покое, если коэффициент трения качения δ = 0,004 м, радиус R = 32,4 см. (40,0)

2.1.98. К однородному катку 1 (рис. 264) весом 5 кН при­ложена пара сил с моментом М = 210 Н·м. Определить, каким должен быть наибольший вес груза 2, для того чтобы каток катился влево, если коэффициент трения качения δ = 0,003 м, радиус R = 0,453 м. (428)

2.1.99. Однородный каток 2 весом 4 кН связан с телом 1 нерастяжимой нитью (рис. 265). Радиус R = 0,5 м, коэффициент трения качения δ = 0,005 м, момент пары сил М = 50 Н·м. Определить наибольший вес тела 1, при котором оно начнет скользить, если коэффициент трения скольжения для катка и тела f = 0,2. (150)

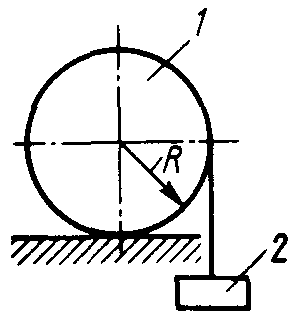
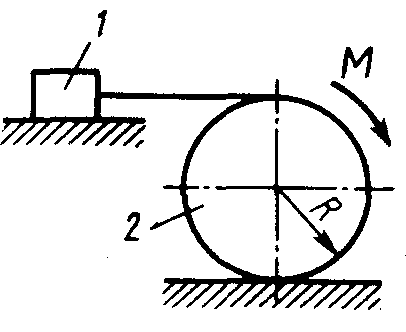
Рис. 263 Рис. 264 Рис. 265

2.1.100. Определить наименьшую силу F (рис. 266), необхо­димую для качения катка радиуса R = 0,3 м, если предельный момент трения качения равен 3,46 Н·м, угол

α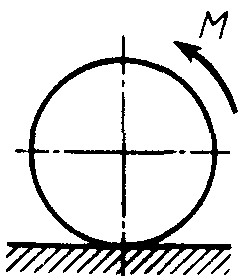 = 30°, расстояние ОА = 0,2 м. (7,99)

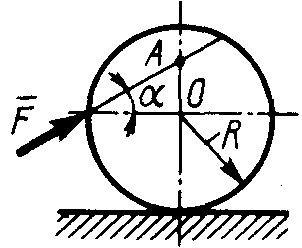
Рис. 266 Рис. 267 Рис. 268

2.1.98. К однородному катку радиуса R = 0,4 м (рис. 267) приложена горизонтальная сила F=12 Н. Каким должен быть наименьший вес катка в кН, для того чтобы он находился в покое, если коэффициент трения качения δ = 0,008 м, размер ОА = 0,2 м? (0,9)

2.1.99. К однородному катку весом 4 кН (рис. 268) прило­жена пара сил с моментом М = 20 Н·м. Опре­делить наименьший коэффициент трения каче­ния, при котором каток находится в покое. (5.10^-3)

2.1.100. К однородному катку весом 4 кН (рис. 269) прило­жена горизонтальная сила F = 50 Н и пара сил с моментом М = 20 Н·м. Определить наимень­ший радиус R катка, при котором он будет катиться влево, если коэф-фициент трения качения δ = 0,005 м и ОА = 0,6R. (0,50)

2.1.101. К однородному катку, малый радиус которого 0,2 м (рис. 270), подвешен груз 1 весом 200 Н и приложена пара сил с моментом М = 57,6 Н·м. Определить в кН наибольший вес катка, при котором он будет катиться влево, если коэффициент трения качения δ = 0,008 м. (2,0)

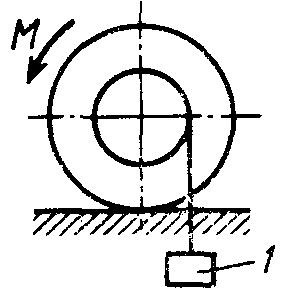
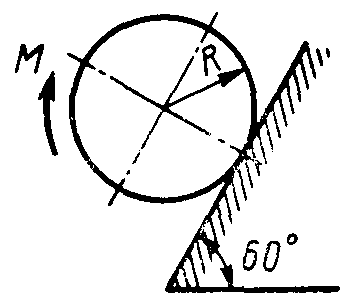
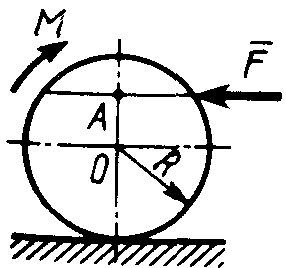
Рис. 269 Рис. 270 Рис. 271

2.1.102. К однородному катку (рис.271) радиуса R = 0,4 м приложена пара сил с моментом М = 210 Н·м. Каким должен быть наибольший вес катка, для того чтобы он мог катиться вверх по наклонной плоскости, если коэффициент тре­ния качения δ = 0,006 м? (601)

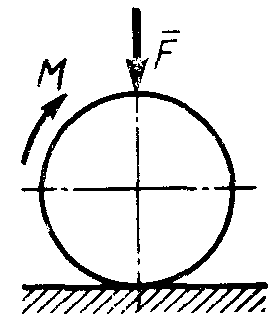
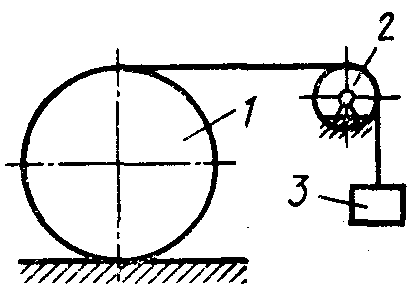
Рис. 272 Рис. 273 Рис. 274

2.1.103. Однородный каток (рис. 272), к которому приложе­на пара сил с моментом М = 18 Н·м, прижи­мается к опорной плоскости силой F = 600 Н. Каким должен быть наибольший вес катка в кН, при котором он будет катиться, если коэффициент трения качения δ = 0,006 м. (2,40)

2.1.104. Однородный каток 1 весом 10 кН и ради­усом 0,5м (рис. 273) связан с грузом 3, вес которого равен 80 Н, горизонтальной нерастяжимой нитью, перекинутой через блок 2. Определить наименьший коэффициент трения качения, при котором каток останется в покое. (0,008)

2.1.105. На конец кабеля (рис. 274), намотанного на барабан, действует сила F = 20 Н. Барабан катится рав­номерно по горизонтальной плоскости без скольжения. Определить в кН вес барабана, если его радиусы r = 0,5 м и R = 1 м. Коэф­фициент трения качения барабана δ = 0,01 м. (3,0)