2.2.3. Равновесие плоских механизмов

2.2.30. Укажите максимальное число независимых неизвестных для механизма, состоящего из двух тел и находящегося в равновесии под действием плоской системы сил? (6)

2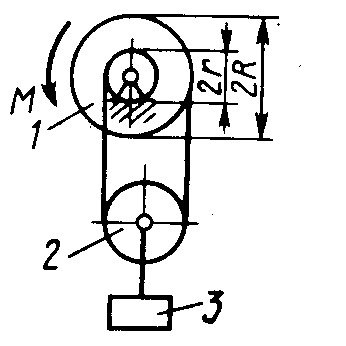 .2.31. Определить момент М пары сил (рис. 294), который необходимо приложить к барабану 1 диффе­ренциального ворота для равномерного подъ­ема груза 3 весом 2·10³ Н, если радиусы R = 15 см и r =10 см. Весом блока 2 пренебречь. (50)

Рис. 294 Рис. 295 Рис. 296

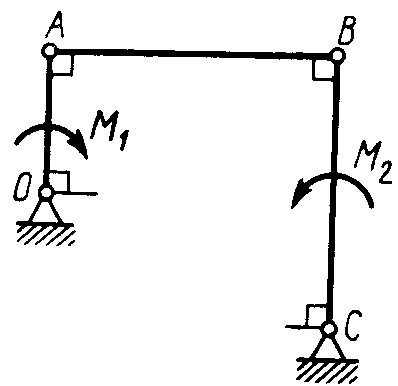
2.2.32. На звено ВС шарнирного четырехзвенника (рис. 296) действует пара сил с моментом M₂ = 200 Н·м. Определить момент М₁ пары сил, который надо приложить к кривошипу ОА, для того чтобы механизм находился в равновесии, если длины звеньев ВС = 2 ОА = 400 мм. (100)

2.2.33. Шарнирный четырехзвенник (рис. 296), весом кото­рого можно пренебречь, находится в равнове­сии. Определить силу F, если к кривошипу ОА приложена пара сил с моментом М = 10 Н·м, а размеры ОА = 10 см, ВС = CD, угол α = 30°. (400)

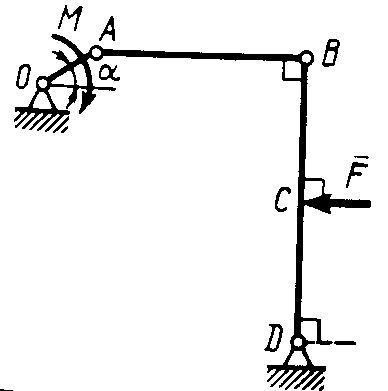
2.2.34. На толкатель I кулачкового механизма (рис. 297) действует сила F = 100 Н. При каком моменте М пары сил, приложенных к кулачку 2, воз­можно равновесие механизма, если расстояние ОА = 10см. (7,07)

2.2.35. На призму 1 (рис. 298) действует сила F₁= 100 Н. Определить силу F₂, которую необходимо приложить к стержню 2, шарнирно связанному с роликом 3, для равновесия системы. (173)

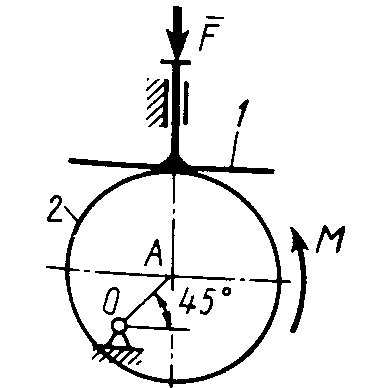
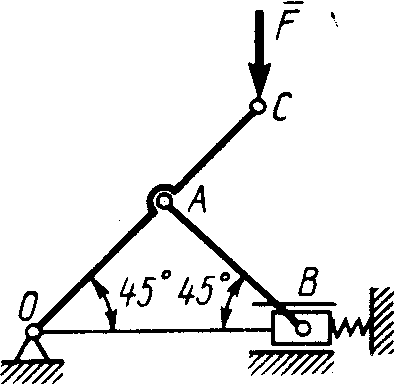
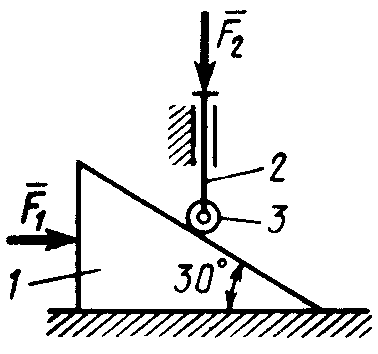
Рис. 297 Рис. 298 Рис. 299

2.2.36. Определить силу упругости пружины в кН при равновесии механизма (рис. 299), если сила взаимно­го давления кривошипа ОАС и шатуна АВ в шарнире А равна 1 кН. (0,707)

2.2.37. Кривошипно-ползунный механизм (рис. 300) нахо­дится в равновесии. Определить в кН силу взаимодействия кривошипа ОАС и шатуна АВ, если к точке С приложена вертикальная сила F₁ = 1 кН, размеры ОА = АС = 0,3 м, угол α =45°. (1,41)

2.2.38. Кулисный механизм (рис.301) находится в равновесии под действием сил F ₁= 1 кН и F₂. Опре­делить в кН силу давления втулки 1 на верти­кальный стержень 2, если углы φ = 30°, α = 60°, длины О = 0,5 м, ОД = 1,2 м. (2,08)

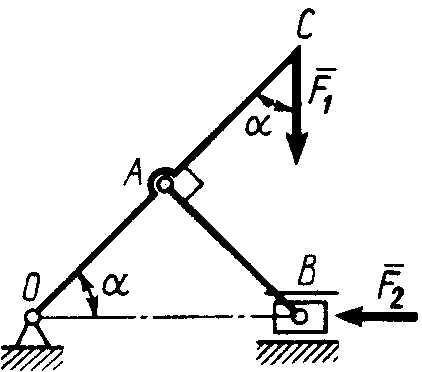
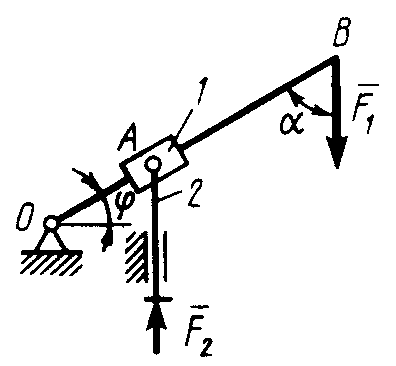
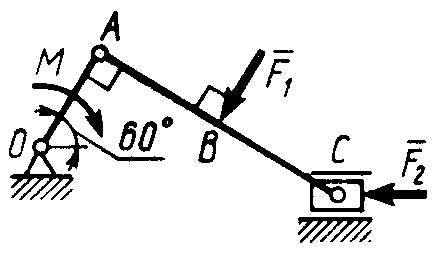
Рис. 300 Рис. 301 Рис. 302

2.2.38. Кривошипно-ползунный механизм (рис. 302) нахо­дится в состоянии равновесия под действием пары сил с моментом М, сил F₁ = 200 Н и F₂ = 500 Н. Определить силу воздействия поршня С на направляющую, если расстояния АВ = ВС = 30 см. (404)

2.3. Фермы

2.3.1. Статически определимые и статически неопределимые фермы. Ненагруженные стержни

Фермой называется конструкция из стержней, соединенных между собой по концам шарнирно и образующих геометрически неизменяемую систему.

Фермой без лишних стержней называется такая ферма, в которой при удалении любого стержня нарушается ее геометрическая неизменяемость. Каждый стержень фермы испытывает только сжатие или растяжение, если выполняются следующие условия:

1. Все стержни прямолинейные.

2. Трение в шарнирах отсутствует.

3. Заданные (активные) силы лежат в плоскости фермы (рассматриваем плоские фермы) и приложены только к узлам фермы.

4. Весом каждого стержня можно пренебречь по сравнению с силами, приложенными к узлам фермы.

5. Ферма без лишних стержней является фермой статически определимой. Это условие выражается формулой:

т = 2 п – 3,

где т – число стержней фермы, п – число узлов фермы.