
- •1. Вычисление определителей
- •1.1. Вычислить определитель второго порядка
- •1.2. Вычислить определитель третьего порядка двумя способами:
- •1.3. Вычислить определитель, предварительно выполнив элементарные преобразования.
- •2. Действия над матрицами
- •2.1. Сложение и вычитание матриц
- •2.2. Умножение матрицы на число
- •2.3. Умножение матриц
- •Алгоритм вычисления произведения матрицы на матрицу :
- •Свойства операции умножения матриц
- •2.4. Возведение матрицы в целую положительную степень
- •2.5. Транспонирование матрицы
- •2.6. Вычисление обратной матрицы
- •Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)
- •Алгоритм построения обратной матрицы с помощью элементарных преобразований строк матрицы
- •2.7. Вычисление ранга матрицы
- •Вычисление ранга матрицы методом окаймления миноров
- •3. Решение систем линейных уравнений
- •3.1. Решить систему линейных уравнений методом обратной матрицы (матричным методом)
- •3.2. Решить систему линейных уравнений по формулам Крамера.
- •3.3. Решить систему линейных уравнений методом Гаусса
- •4. Решение произвольных систем линейных уравнений
- •4.1. Исследовать на совместность и решить неоднородные системы линейных уравнений
- •4.2. Исследовать и решить системы линейных однородных уравнений
- •5. Линейная зависимость и независимость векторов
- •6. Вычисление собственных значений и собственных векторов заданных матриц
4. Решение произвольных систем линейных уравнений
При решении произвольных систем линейных уравнений первым делом проверяем систему уравнений на совместность, для этого воспользуемся теоремой Кронекера-Капелли:
Теорема: Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.
Следующий шаг: 1) если система не совместна, то делаем вывод, что система решений не имеет; 2) если система совместна и ранг ее матрицы равен r, то для решения системы руководствуемся правилом:
выбираем из всех уравнений системы r уравнений, матрица из коэффициентов при неизвестных у которых имеет ранг r. В левых частях этих уравнений оставить такие r неизвестных, что определитель из коэффициентов при них отличен от нуля. Переменные, оставленные в левых частях уравнений называются базисными переменными. Остальные неизвестные объявить свободными и перенести в правые части уравнений. Решить систему дальше – это значит выразить переменные, оставленные в левых частях уравнений, через свободные переменные. Получим, так называемое, общее решение системы. Далее, давая свободным переменным произвольные значения и вычисляя значения базисных переменных, например, по формулам Крамера, можно получить все частные решения системы.
4.1. Исследовать на совместность и решить неоднородные системы линейных уравнений
Примеры выполнения заданий:
1) Дано:

Решение: Запишем
расширенную матрицу
![]() системы, совмещенную с матрицей А
системы:
системы, совмещенную с матрицей А
системы:
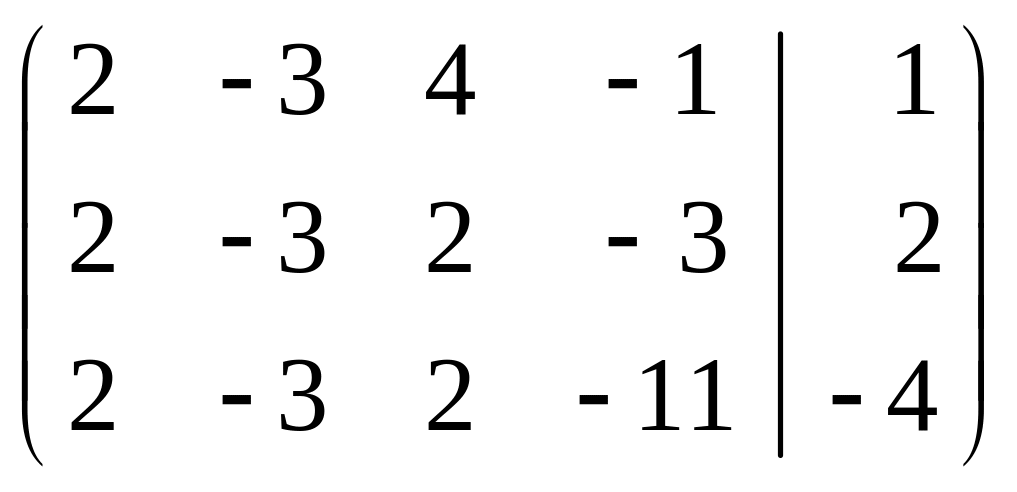 .
.
Вычислим ранги обеих матриц методом приведения их к ступенчатому виду с помощью элементарных преобразований строк. С этой целью первую строку вычтем из второй, а вторую – из третьей, получим:
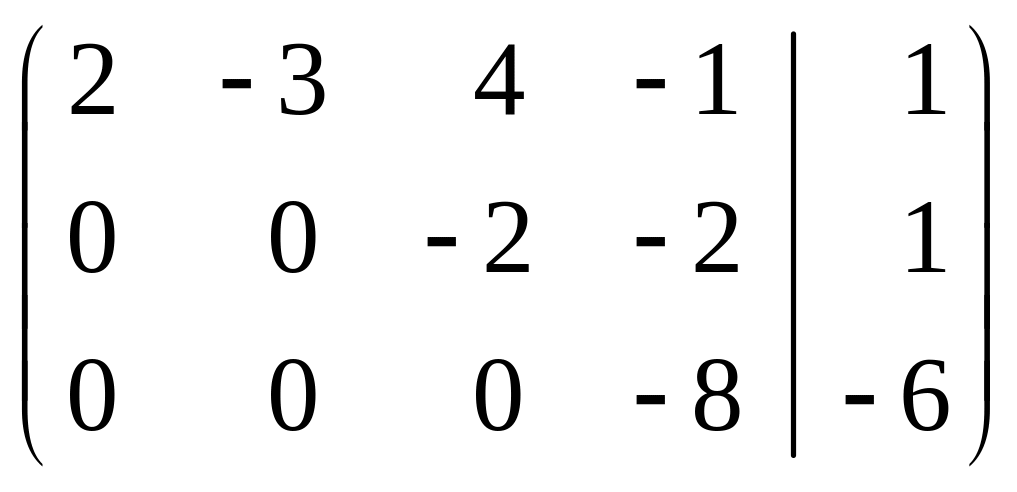 или
или
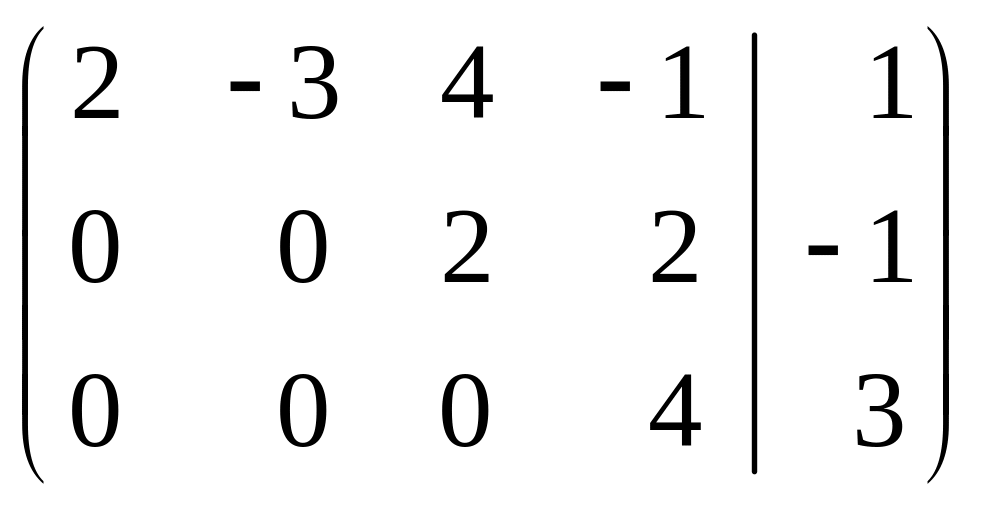 .
.
Отсюда видно, что как матрица системы А, так и расширенная матрица имеют одинаковый ранг, равный трем. Делаем вывод, что заданная система совместна, причем все три ее уравнения являются линейно независимыми (число уравнений и ранг матрицы совпадают). Таким образом, заданная система эквивалентна следующей системе:

Вычисляя определители матрицы этой системы:
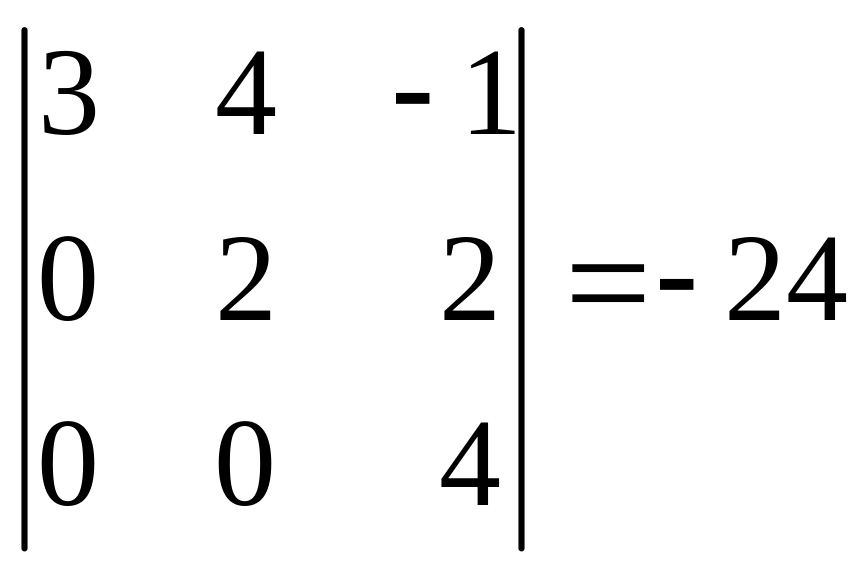
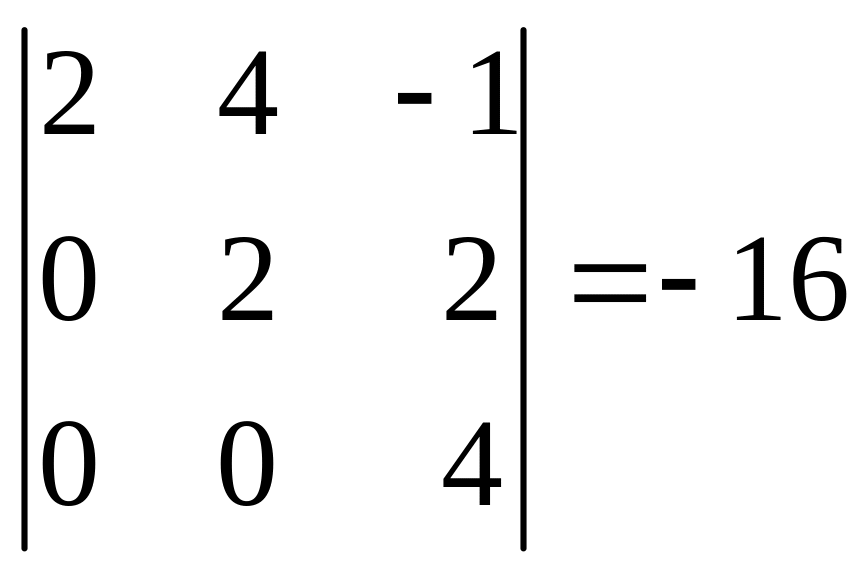
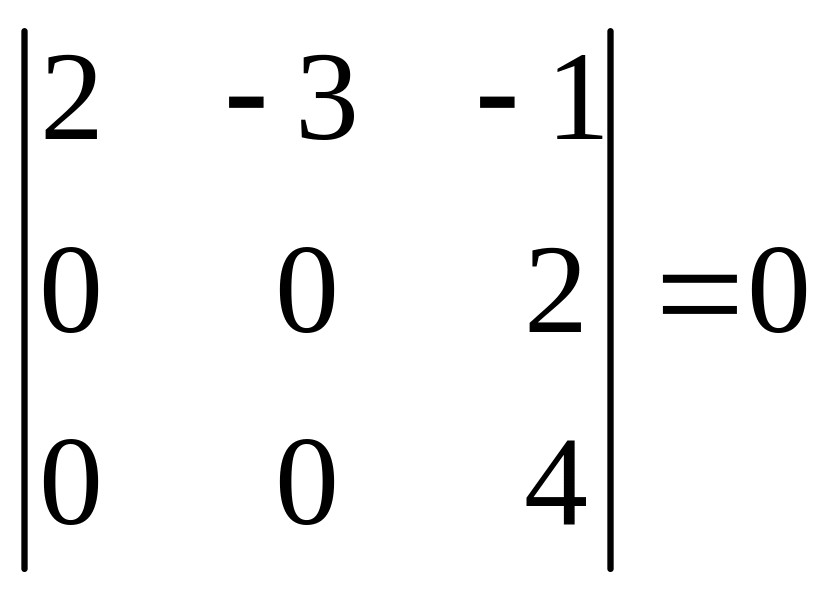
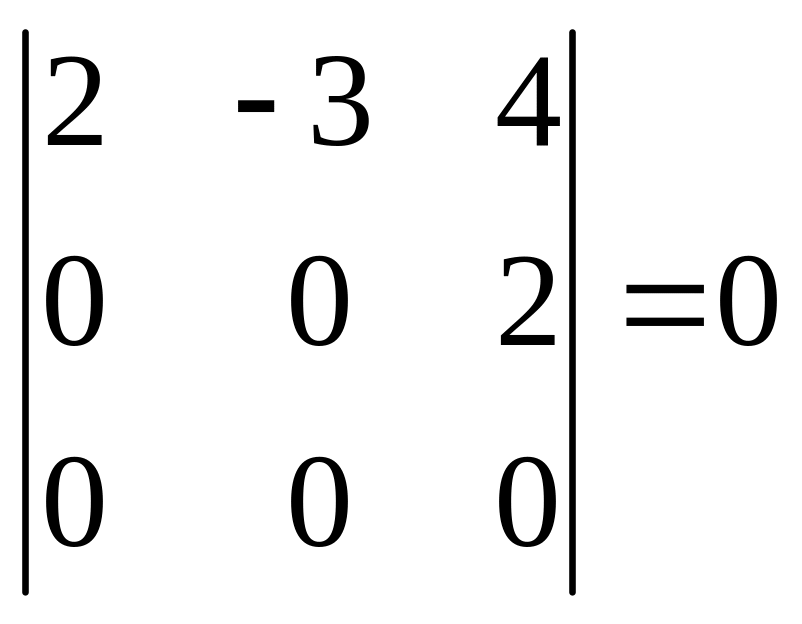
делаем вывод, что
свободной может быть объявлена либо
![]() ,
либо
,
либо
![]() неизвестная. Поэтому в первом уравнении
системы в правую часть следует перенести
неизвестная. Поэтому в первом уравнении
системы в правую часть следует перенести
![]() или
или
![]() .
.
Перенеся , получим:
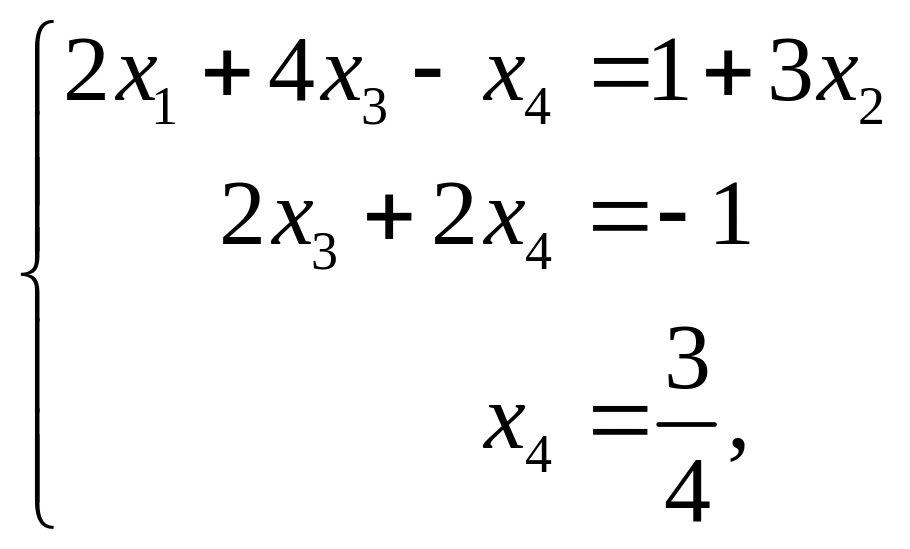
откуда находим:
![]() .
Подставляем во второе уравнение системы.
Получим
.
Подставляем во второе уравнение системы.
Получим
![]()
Подставляем найденные значения и в первое уравнение системы, найдем .
![]() .
.
Записываем общее решение системы:

Найдем какое-нибудь
частное решение. Пусть свободная
переменная
![]() .
Тогда частное решение системы будет
равно
.
Тогда частное решение системы будет
равно
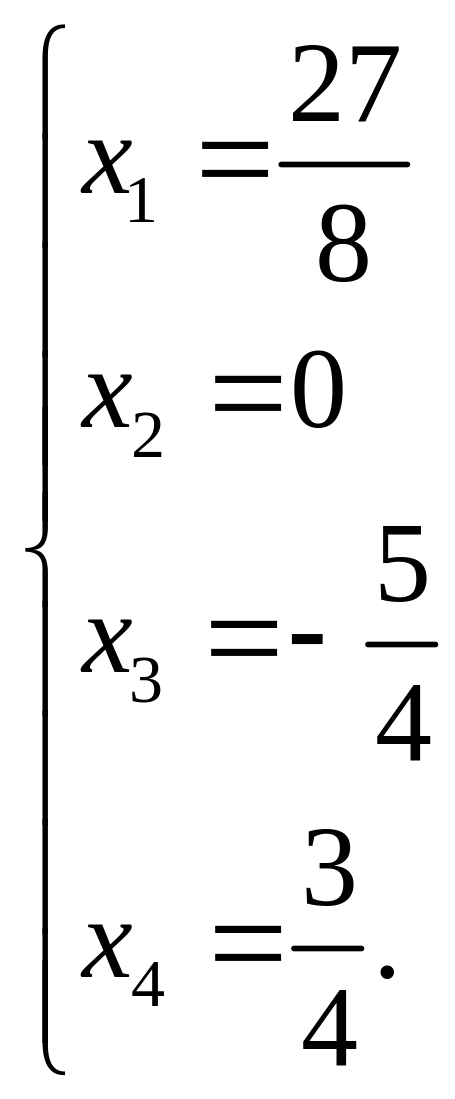
Ответ:
 – общее решение
системы
– общее решение
системы
– частное решение системы.
2) Дано:
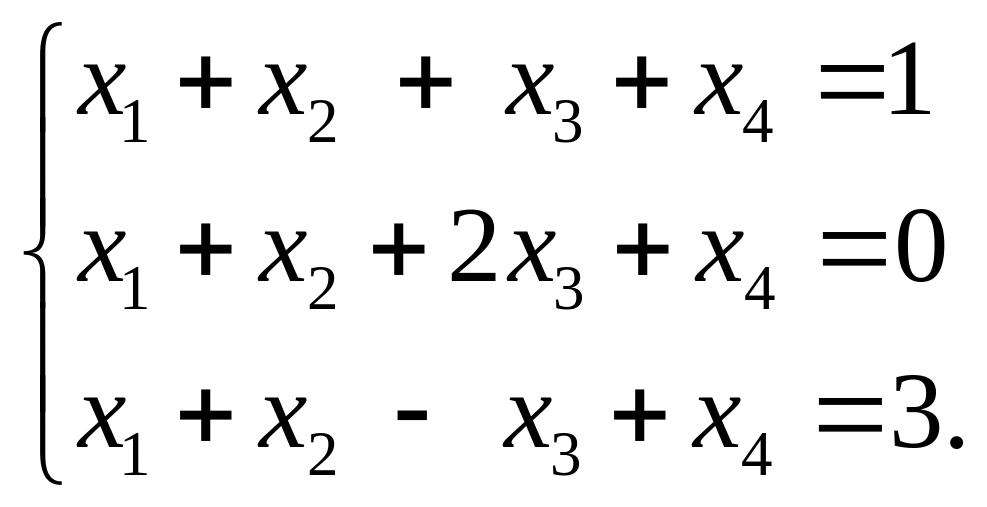
Решение: Запишем расширенную матрицу системы, совместив ее с матрицей А системы
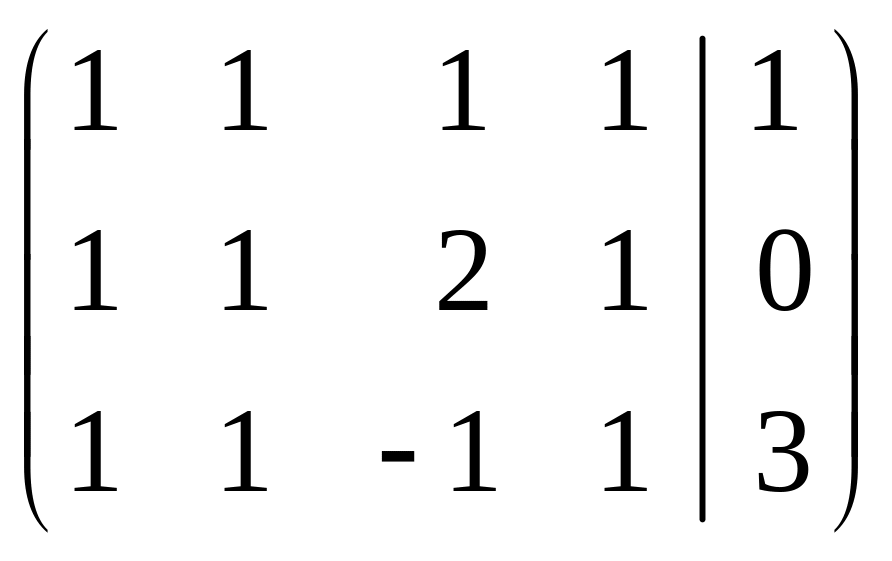 .
.
Выполним элементарные преобразования над строками совмещенных матриц, вычислим ранги матриц:

Получили матрицу, имеющую две ненулевые строки. Видно, что как матрица системы А, так и расширенная матрица имеют одинаковый ранг, равный двум. Делаем вывод, что заданная система линейных уравнений совместна. Вместе с тем линейно независимы только первые два уравнения (ранг равен двум), а третье – следствие двух первых (при элементарных преобразованиях расширенной матрицы ее последняя строка стала нулевой). Таким образом, заданная система эквивалентна следующей системе:
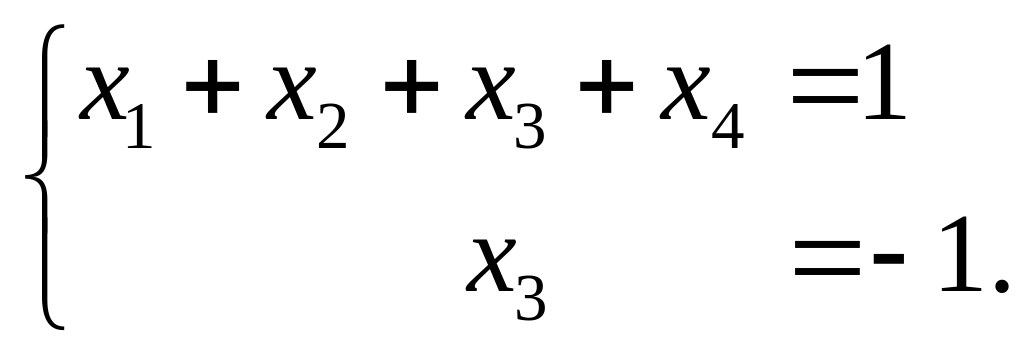
Для решения
полученной системы необходимо определиться
со свободными переменными. Так как ранг
заданной системы
![]() ,
то базисных переменных будет тоже две.
Все остальные – свободные, найдем их.
,
то базисных переменных будет тоже две.
Все остальные – свободные, найдем их.
Вычислим определители второго порядка, составленные из коэффициентов при неизвестных, и отметим отличные от нуля.
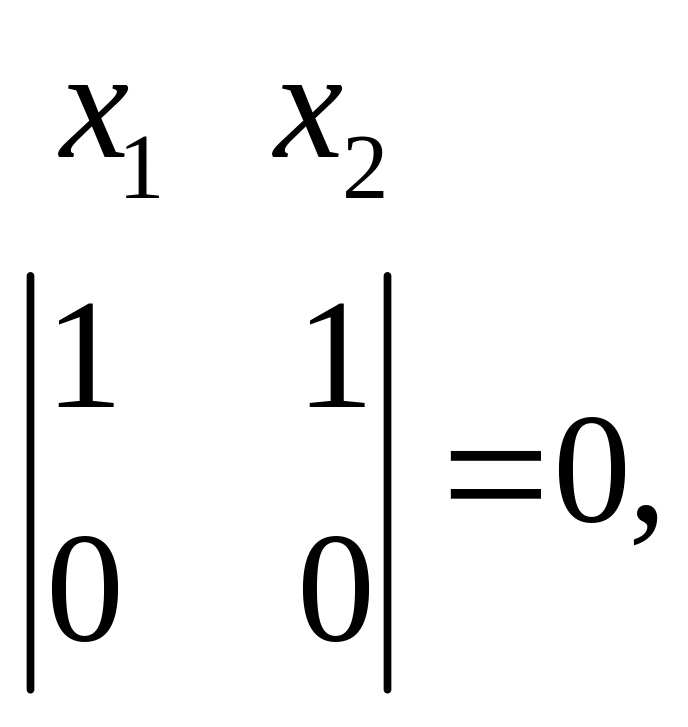
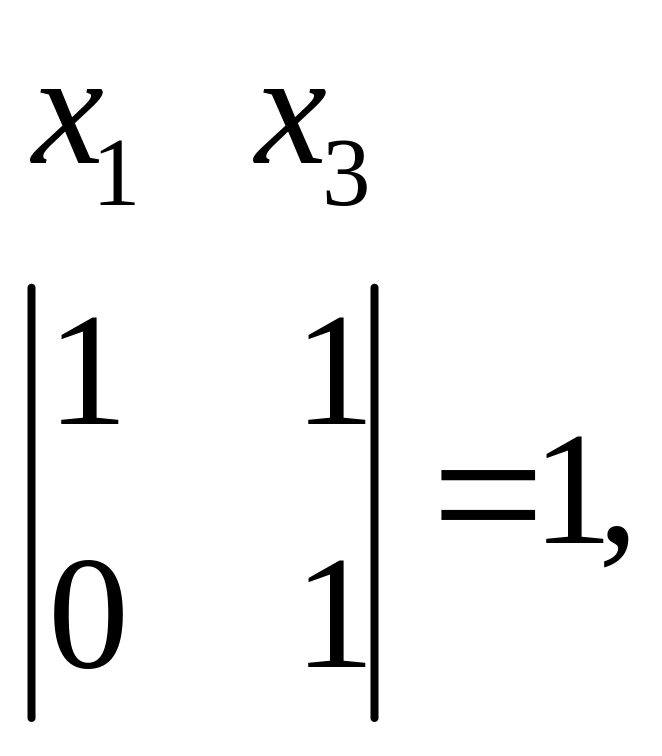
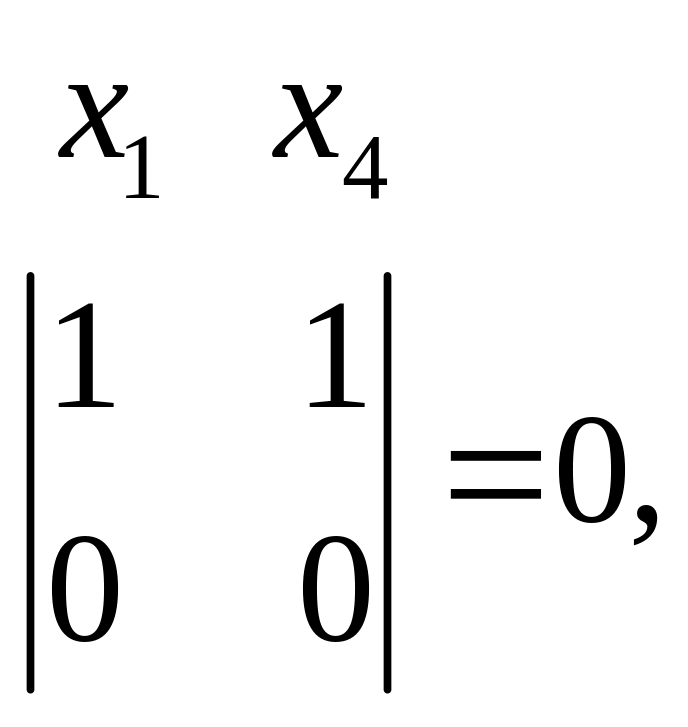
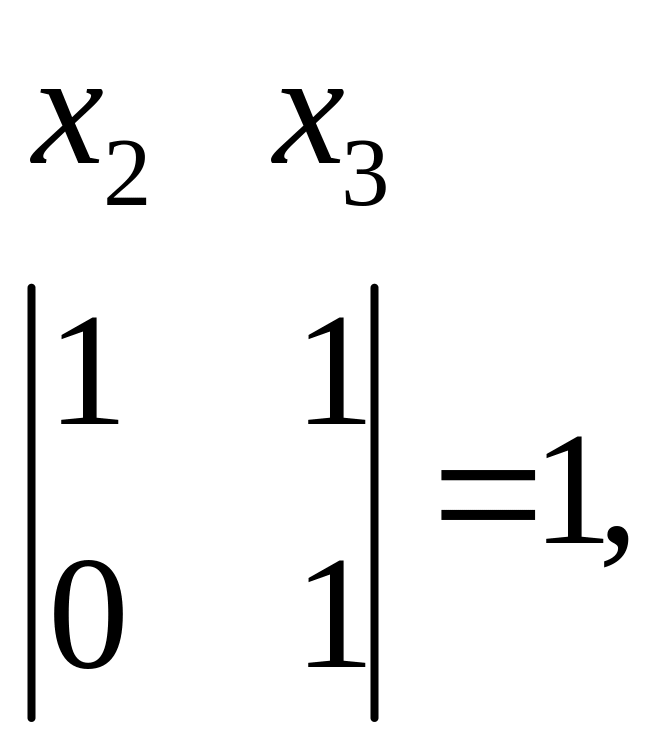
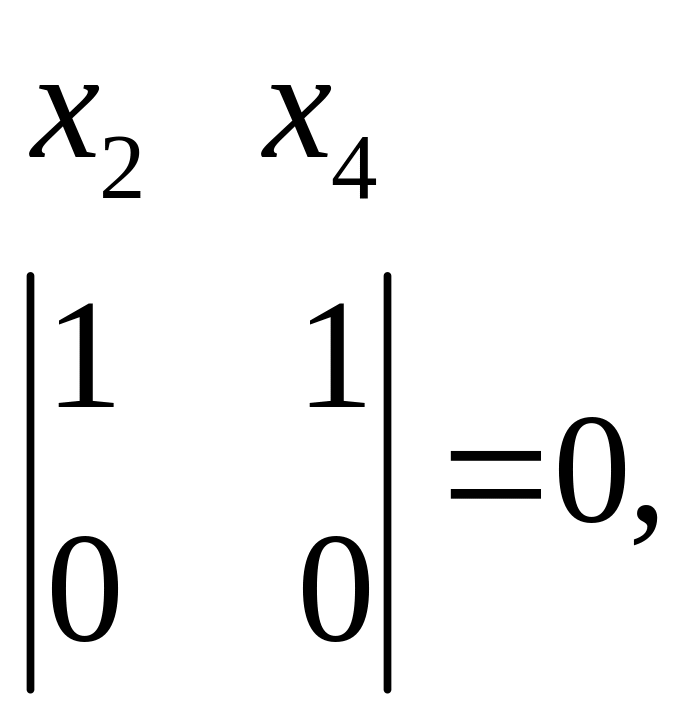

Делаем вывод, что переменная обязательно должна быть базисной. Вторую переменную выбираем произвольно из , , . Пусть будет базисной переменной, тогда и будут свободными, переносим их в правую часть уравнений
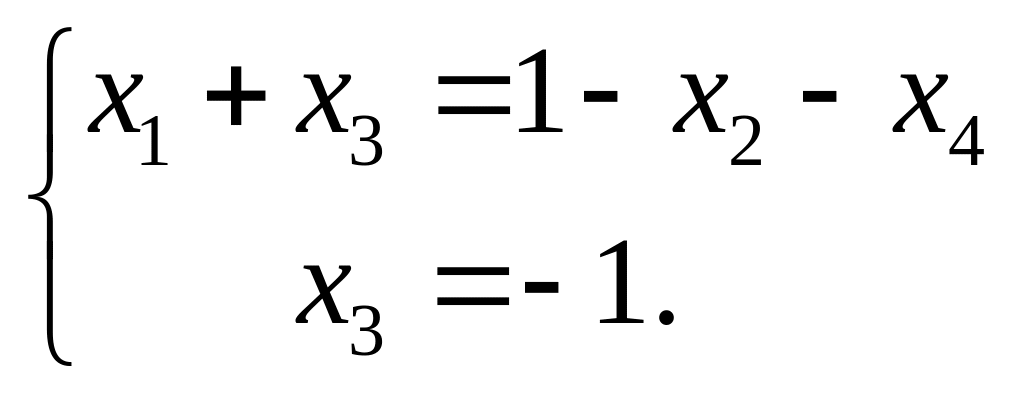
Решая эту систему находим:
![]()
Тогда общее решение системы будет иметь вид:

Найдем какое-нибудь
частное решение. Пусть
,
![]() .
Тогда получим:
.
Тогда получим:
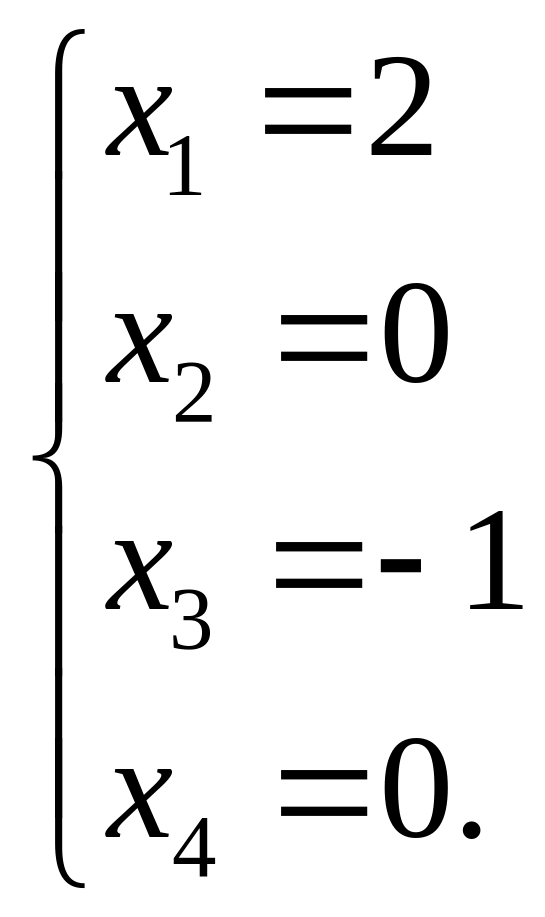
Ответ:
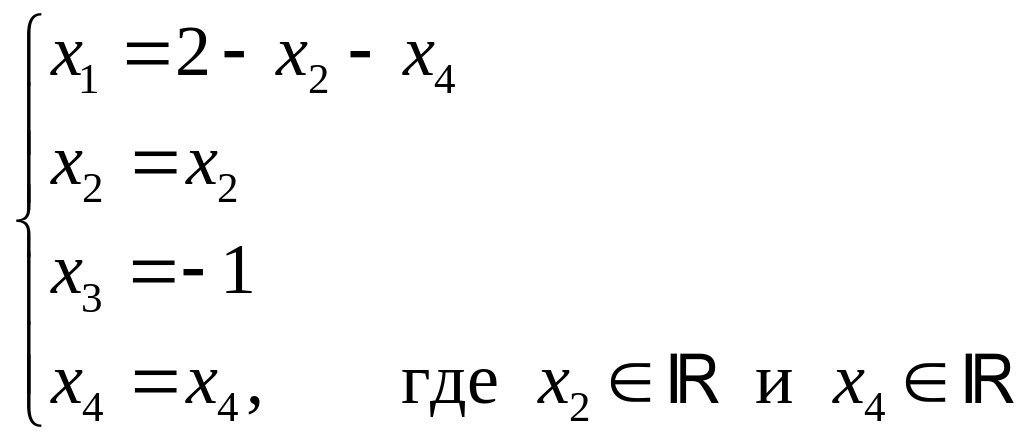 – общее решение системы.
– общее решение системы.
3) Дано:

Решение: Запишем расширенную матрицу системы, совместив ее с матрицей А системы и найдем их ранги:

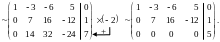
Отсюда видно, что ранг матрицы А заданной системы равен двум (третья строка матрицы А состоит из нулей, а миноры второго порядка отличны от нуля), в то время как ранг расширенной матрицы равен трем. Поэтому, на основании теоремы Кронекера-Капелли, заданная система несовместна, т.е. не имеет решений.
Ответ: система не имеет решений.
4) Дано:
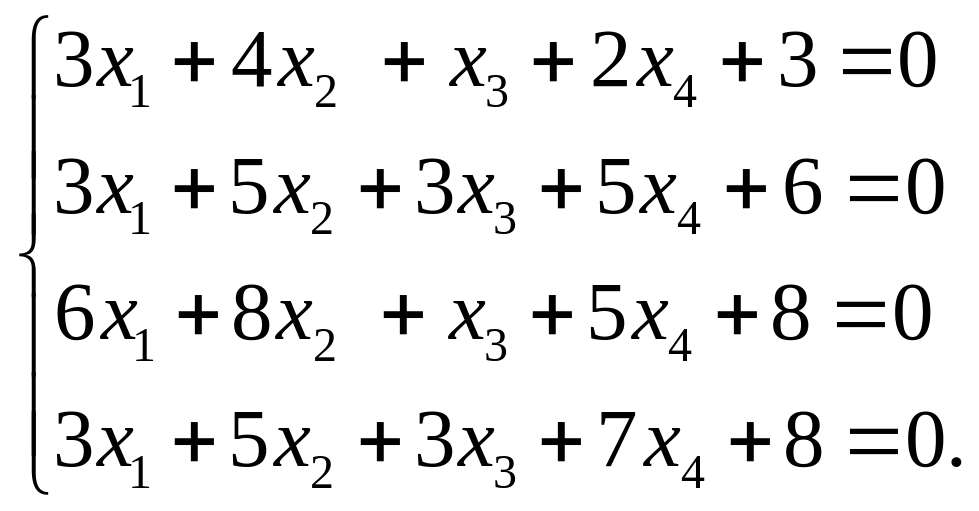
Решение: Запишем расширенную матрицу системы, совместив ее с матрицей А системы, найдем их ранги, делая элементарные преобразования над строками:

Полученный результат свидетельствует, что данная система совместна, так как ранги матриц А и одинаковы и равны четырем. Не трудно заметить, что ранг матрицы системы равен числу уравнений системы, поэтому делаем вывод о том, что все уравнения системы линейно независимы. При этом ранг матрицы системы равен числу неизвестных – это свидетельствует о том, что система имеет единственное решение.
Заданная система эквивалентна следующей:

Решим эту систему:
![]()
![]() .
.
Записываем ответ.
Ответ:
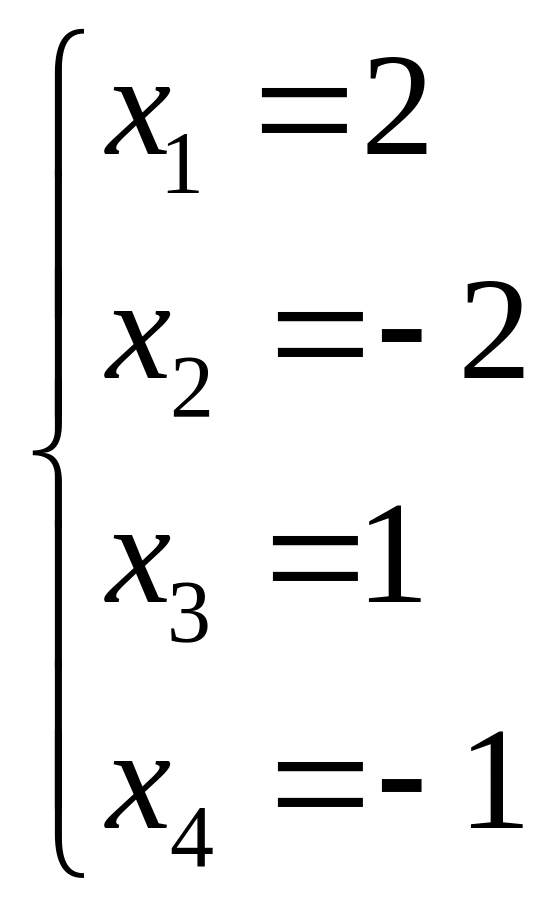 – единственное решение заданной
системы.
– единственное решение заданной
системы.
Для самостоятельного решения:
1.
 2.
2.
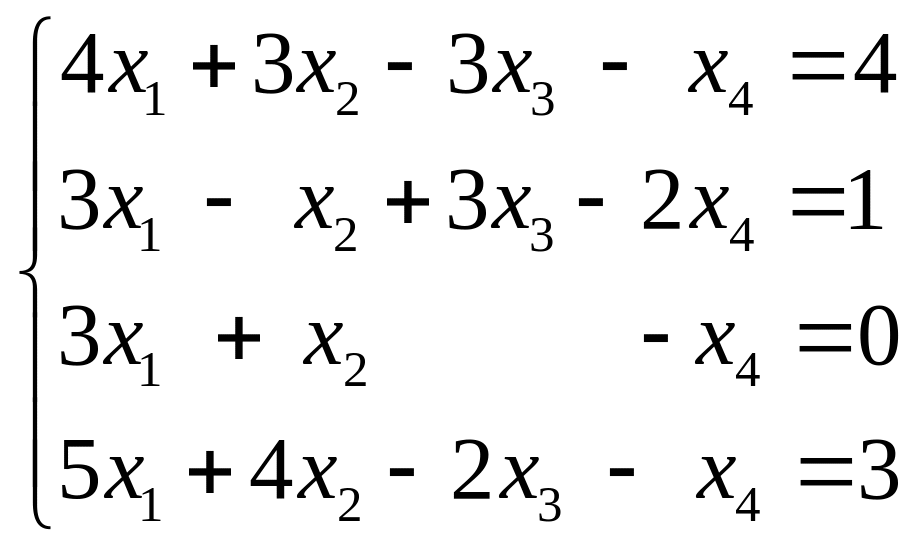
3.
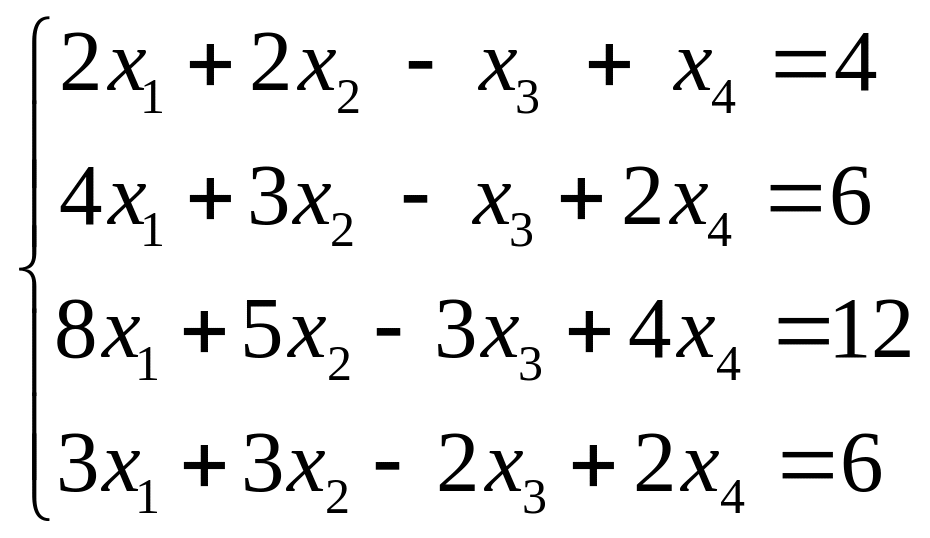 4.
4.
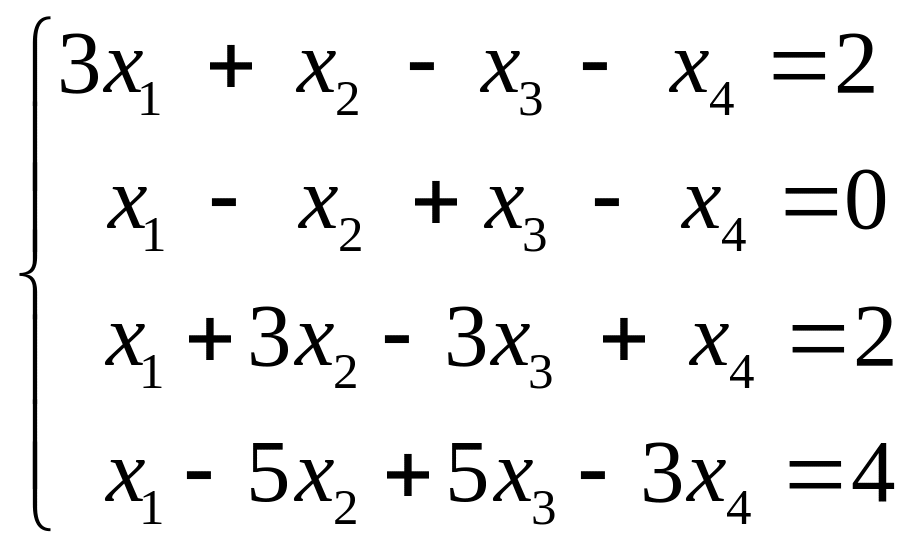
5.
 6.
6.

7.
 8.
8.
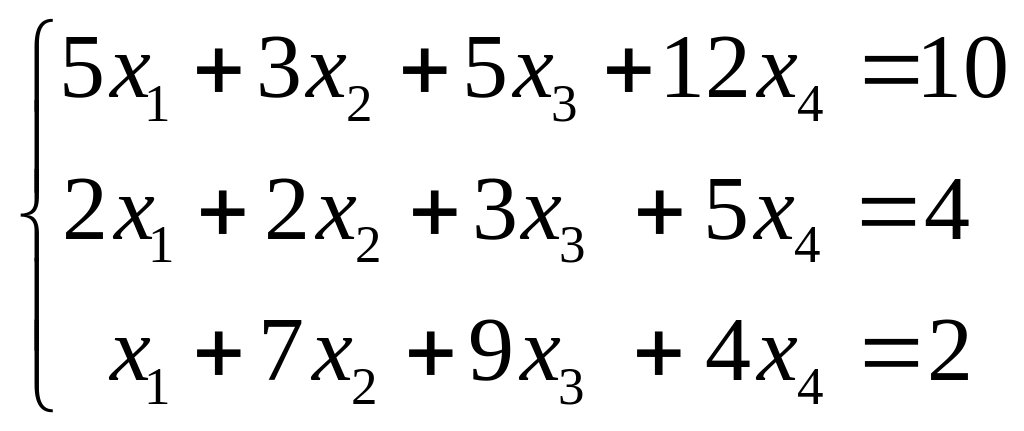
9.
 10.
10.

11.
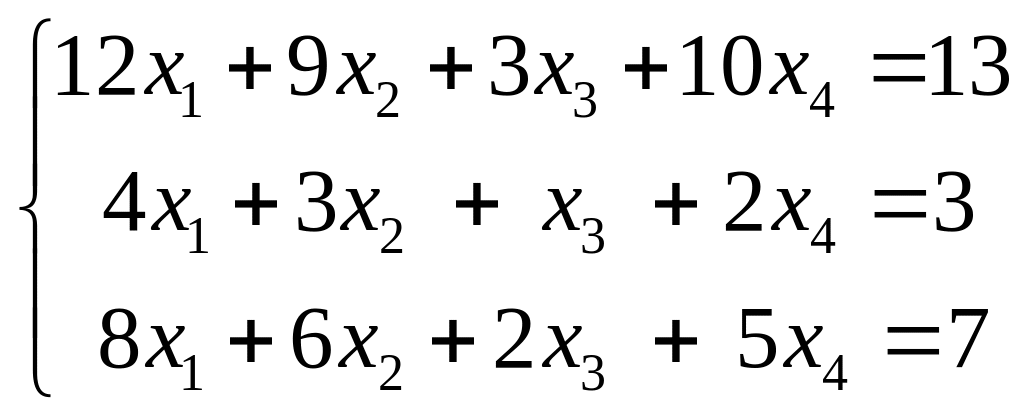 12.
12.
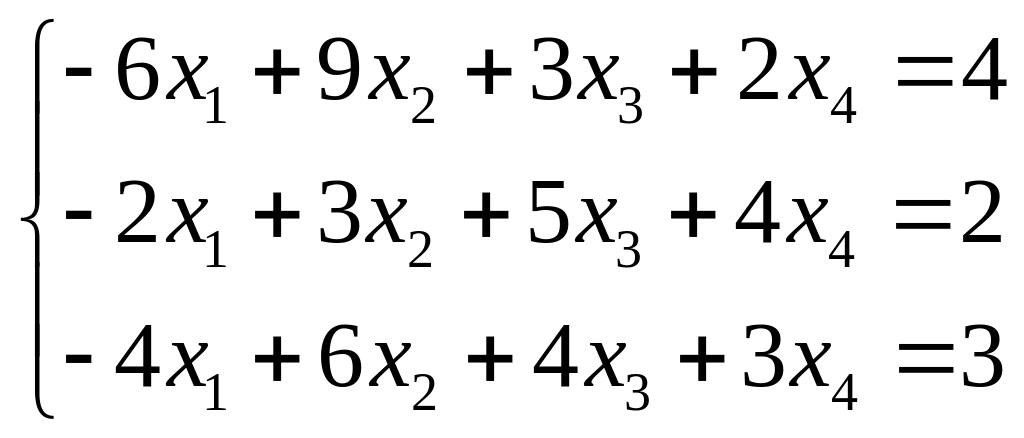
13.
 14.
14.
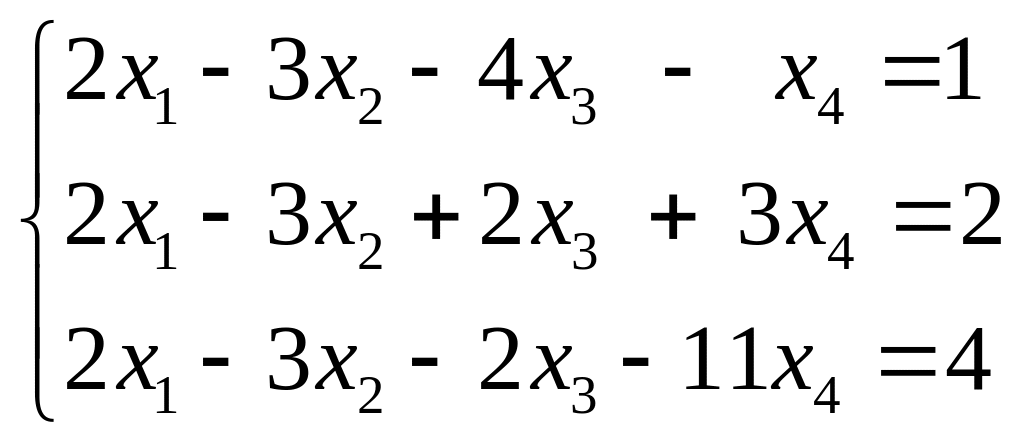
15.
 16.
16.

17.
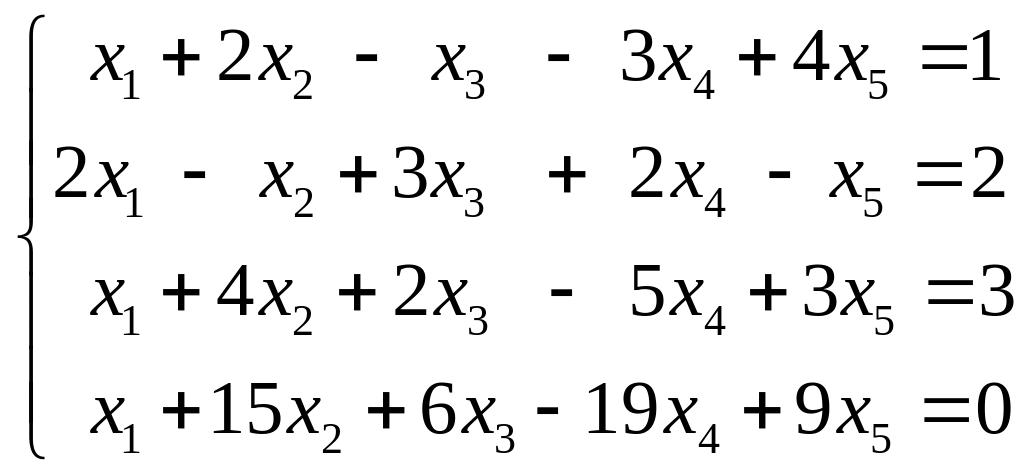 18.
18.

