2.4. Возведение матрицы в целую положительную степень
Операция возведения
квадратной матрицы в степень
определяется в виде:
.
По определению
полагают
.
Легко показать, что
.
Замечание 1.3. Возведение в степень матрицы может привести к нулевой матрице.
Замечание 1.4. Операция возведения в степень определена только для квадратных матриц.
Пример выполнения задания:
Найдите значение матричного многочлена
.
Решение:
Ответ:
.
Для самостоятельного решения:
а) Найдите матрицу
.
1.
; 2.
; 3.
.
б) Найдите значение
матричного многочлена
.
1.
; 2.
;
3.
. 4.
.
2.5. Транспонирование матрицы
Транспонирование – это замена строк столбцами. Например, пусть дана матрица А размерностью :
.
Если в матрице А
поменять местами строки и столбцы, то
получится матрица, транспонированная
к данной, обозначаемая
:
.
Приведем основные свойства операции транспонирования, которые легко доказываются вычислением:
1. Двойное
транспонирование возвращает исходную
матрицу:
.
2. Транспонирование
суммы матриц эквивалентно сумме
транспонирования слагаемых:
.
3. Транспонирование
произведения двух матриц эквивалентно
произведению транспонированных матриц,
взятых в обратном порядке:
.
4. Произведение
матрицы на свою транспонированную
или
всегда имеет результатом симметричную
квадратную матрицу.
5. Если матрица А
– квадратная, то значение ее определителя
не зависит от транспонирования:
.
Примеры выполнения заданий:
Задача 1.
Транспонируйте матрицу
.
Решение:
Записывая первую
и вторую строки матрицы А как первый
и, соответственно, второй столбец матрицы
,
получим матрицу
.
Ответ:
.
Задача 2.
Транспонируйте матрицу
.
Решение:
Так как у матрицы
А две строки и три столбца, то у
матрицы
будет три строки и два столбца:
.
Ответ: .
Для самостоятельного решения:
а) Найдите матрицу
1.
; 2.
;
3.
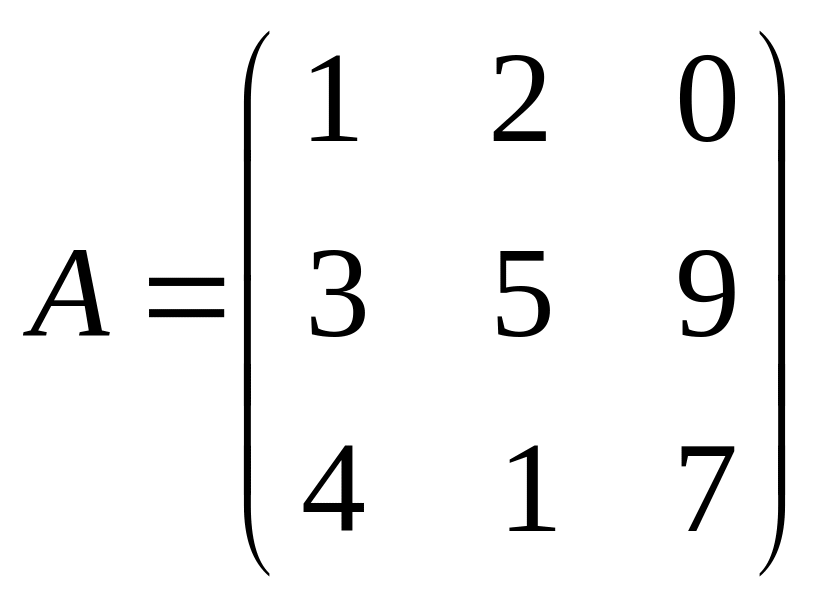; 4.
;
5.
.
б) Найдите произведение матриц и .
1.
; 2.
;
3.
; 4.
.
2.6. Вычисление обратной матрицы
Определение.
Матрица
называется обратной для квадратной
матрицы А, если
.
Матрица А имеет обратную тогда и только тогда, когда её определитель не равен нулю.
Определение. Матрица называется невырожденной, если ее определитель не равен нулю.
Квадратная матрица А, определитель которой не равен нулю, имеет единственную обратную матрицу
,
где
матрицы А.
алгебраическое
дополнение к элементу
матрицы А.
Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)
1. Найти определитель матрицы А. Если определитель отличен от нуля, то матрица имеет обратную матрицу.
2. Поменять местами столбцы матрицы (транспонировать матрицу) А.
3. Найдем алгебраические
дополнения элементов матрицы
.
Заменим каждый элемент матрицы А
его алгебраическим дополнением:
,
– дополнительный минор, он равен
определителю матрицы, которая получается
вычёркиванием i-ой
строки и j-го столбца.
4. Вычисляем
обратную матрицу
.
5. Проверить
правильность вычисления обратной
матрицы по формуле:
.
Примеры выполнения заданий:
Задача 1. Найти
матрицу, обратную к матрице А, если
дана матрица
.
Решение: Применим алгоритм нахождения обратной матрицы.
1. Найти определитель матрицы А. Если определитель отличен от нуля, то матрица имеет обратную матрицу.
Матрица имеет
обратную матрицу, так как
.
2. Найдем матрицу
,
транспонированную к матрице А:
.
3. Найдем алгебраические
дополнения элементов матрицы
.
Заменим каждый элемент матрицы А
его алгебраическим дополнением:
,
– дополнительный минор, он равен
определителю матрицы, которая получается
вычёркиванием i-ой
строки и j-го столбца.
.
4. Вычисляем обратную матрицу .
5. Проверим правильность вычисления обратной матрицы по формуле:
.
Ответ:
Задача 2.
Найдите матрицу, обратную к данной
матрице
.
1. Найдем
.
2. Найдем матрицу :___________________________.
3. Найдем алгебраические дополнения элементов матрицы :___________________ .
4. Вычисляем обратную матрицу :
_____________________________________________________________________________
.
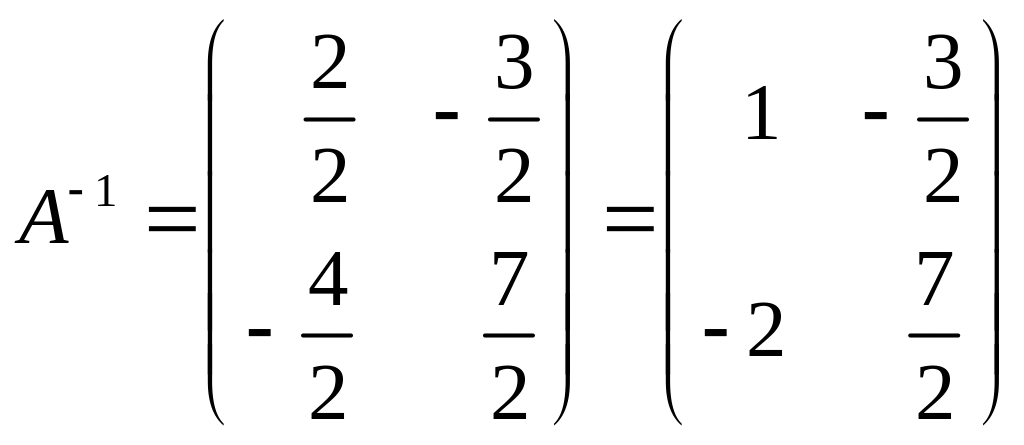5. Проверим правильность вычисления обратной матрицы по формуле:
______________________________________________________________________________.
Ответ:
.
Элементарными преобразованиями строк (столбцов) матрицы называются:
а) умножение i-ой строки (столбца) матрицы на число ;
б) прибавление к i-ой строке (столбцу) j-ой строки (столбца), умноженной на ;
в) перестановка i-ой и j-ой строк (столбцов) матрицы.