Вычисление ранга матрицы методом окаймления миноров
1. Найти ненулевой
элемент матрицы (если такого нет, то
);
2. Вычислить миноры второго порядка, которые окаймляют выбранный элемент;
3. Если среди
вычисленных миноров второго порядка
имеется отличный от нуля, рассмотреть
все миноры третьего порядка, окаймляющие
какой-нибудь минор второго порядка, не
равный нулю. Продолжать так далее, пока
все миноры, окаймляющие не нулевой минор
-го
порядка, не будут равны нулю. В этом
случае ранг матрицы равен
.
Примеры выполнения заданий:
Задача 3. Найдите
ранг матрицы методом окаймляющих
миноров, и укажите какой – либо базисный
минор
.
Решение:
Так как у матрицы
A есть ненулевые
элементы, то
.
Найдём какой – либо ненулевой минор
второго порядка (если он существует).
Таким минором является, например,
.
Значит,
.
Вычислим миноры
третьего порядка, окаймляющие
:
.
Все миноры третьего
порядка, окаймляющие
,
равны нулю, следовательно,
.
Итак,
.
Одним из базисных
миноров является
.
Ответ:
;
.
Задача 4. Найти
,
если
.
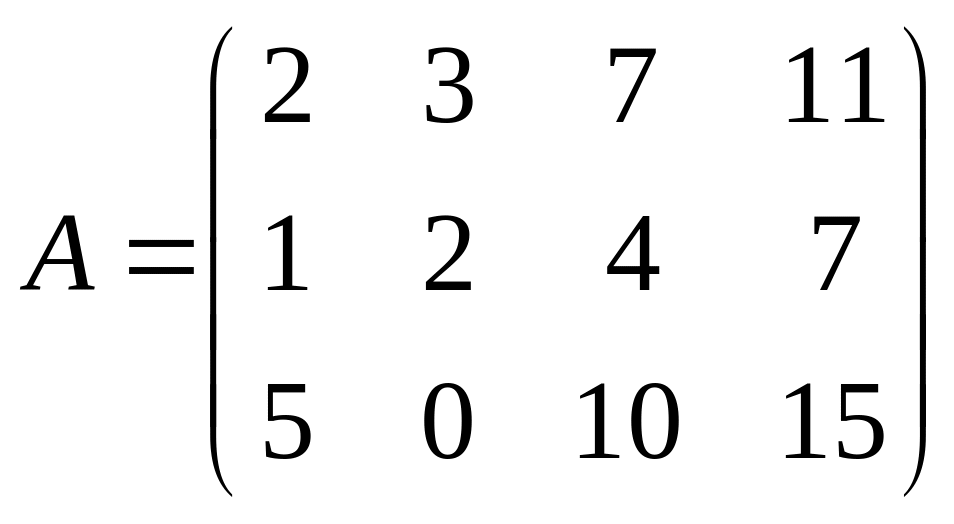Решение:
.
.
Ответ: .
Задача 5.
Найти
,
если
.
.
,
Ответ:
.
Для самостоятельного решения:
1. Приведите к ступенчатому виду матрицу.
а)
; б)
.
в)
; г)
.
2. Найдите ранг матрицы методом элементарных преобразований.
а)
; б)
;
в) ; г) .
3. Найдите ранг матрицы методом окаймляющих миноров, и укажите какой – либо базисный минор.
а)
; б)
.
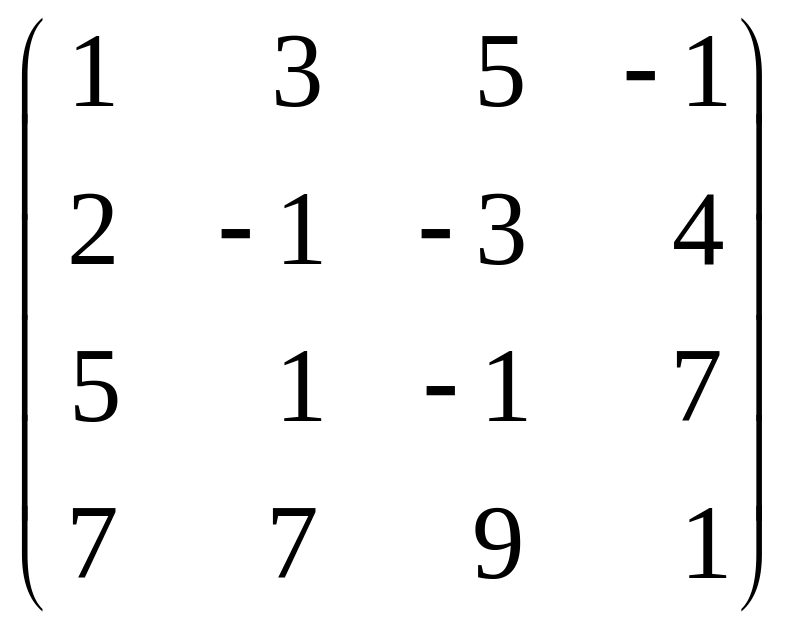3. Решение систем линейных уравнений
3.1. Решить систему линейных уравнений методом обратной матрицы (матричным методом)
Рассмотрим систему уравнений
(3.1)
Данная система
может быть записана в матричном виде
,
где
Тогда решение
системы (3.1.) имеет вид
(
- обратная матрица).
Примеры выполнения заданий:
Решить систему методом обратной матрицы (матричным методом)
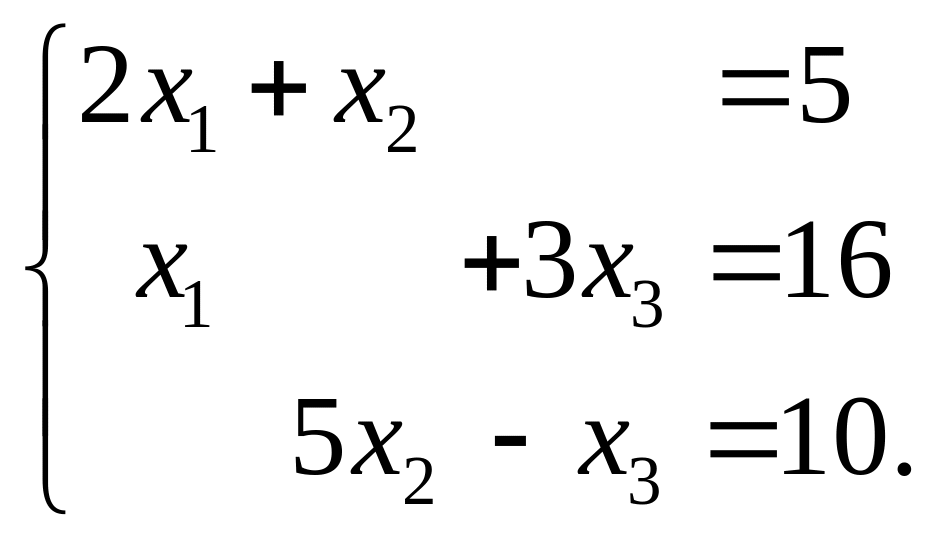
Решение: Найдем матрицу обратную матрице системы:
.
Алгебраические дополнения
, 
, 
, 
, 
,
, 
, 
.
Матрица из алгебраических дополнений
.
Обратная матрица
Находим решение системы
,
,
Ответ: , , .
3.2. Решить систему линейных уравнений по формулам Крамера.
Рассмотрим систему трёх линейных уравнений с тремя неизвестными
Система имеет
единственное решение при условии, что
определитель системы отличен от нуля,
т.е.
,
которое определяется по формулам
(3.2)
где
.
Формулы (3.2) называются формулами Крамера.
Примеры выполнения заданий:
Задача 1. Решить систему линейных уравнений по формулам Крамера
Решение: Найдем определитель матрицы системы
.
Выпишем столбец
свободных членов
Заменим первый столбец матрицы А на столбец из свободных членов и вычислим полученный определитель
.
Тогда
.
Заменим второй столбец матрицы А на столбец из свободных членов и вычислим полученный определитель
.
Находим неизвестную
.
Для нахождения
неизвестной
в матрице А заменяем _________ столбец
на столбец из ____________.
.
Находим неизвестную
.
Ответ:
,
,
.
Задача 2. Приведено решение системы
по формулам Крамера
,
,
;
,
.
Найти значения а, b, x и y.