
- •1. Вычисление определителей
- •1.1. Вычислить определитель второго порядка
- •1.2. Вычислить определитель третьего порядка двумя способами:
- •1.3. Вычислить определитель, предварительно выполнив элементарные преобразования.
- •2. Действия над матрицами
- •2.1. Сложение и вычитание матриц
- •2.2. Умножение матрицы на число
- •2.3. Умножение матриц
- •Алгоритм вычисления произведения матрицы на матрицу :
- •Свойства операции умножения матриц
- •2.4. Возведение матрицы в целую положительную степень
- •2.5. Транспонирование матрицы
- •2.6. Вычисление обратной матрицы
- •Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)
- •Алгоритм построения обратной матрицы с помощью элементарных преобразований строк матрицы
- •2.7. Вычисление ранга матрицы
- •Вычисление ранга матрицы методом окаймления миноров
- •3. Решение систем линейных уравнений
- •3.1. Решить систему линейных уравнений методом обратной матрицы (матричным методом)
- •3.2. Решить систему линейных уравнений по формулам Крамера.
- •3.3. Решить систему линейных уравнений методом Гаусса
- •4. Решение произвольных систем линейных уравнений
- •4.1. Исследовать на совместность и решить неоднородные системы линейных уравнений
- •4.2. Исследовать и решить системы линейных однородных уравнений
- •5. Линейная зависимость и независимость векторов
- •6. Вычисление собственных значений и собственных векторов заданных матриц
3.3. Решить систему линейных уравнений методом Гаусса
Примеры выполнения заданий:
Задача 1. Решить систему методом Гаусса

Решение: Запишем расширенную матрицу системы
 .
.
В каждой строчке
выбираем первый ненулевой элемент и
под ним зануляем все элементы, используя
элементарные преобразования. Начинаем
с первой строки. Обводим первый ненулевой
и обозначаем
 элементы, подлежащие занулению
элементы, подлежащие занулению

Сравниваем элементы первого столбца. Первую строку умножаем на 5 и из нее вычитаем семь вторых строк
![]()
![]()
Эту строку записываем вместо второй.
Первую строку умножаем на 10 и из нее вычитаем семь третьих строк
![]()
![]()
Эту строку запишем вместо третьей. После преобразования имеем

Выбираем первый ненулевой элемент второй строки

Умножаем вторую строку на 97 и вычитаем из нее третью строку, умноженную на 31
![]()
![]()
Результат запишем вместо третьей строки

Матрица системы приведена к верхнетреугольному виду. Запишем эквивалентную систему

Поднимаемся от последнего уравнения к первому:
1)
![]() ,
,
![]() ,
,
2)
![]()

3)
![]()

Ответ:
![]() ,
,
![]() ,
,
![]() .
.
Задача 2. Решить систему методом Гаусса

Решение: Запишем расширенную матрицу системы
 .
.
О бведем
первый ненулевой элемент первой строки
и укажем знаком
элементы, которые нужно занулить
бведем
первый ненулевой элемент первой строки
и укажем знаком
элементы, которые нужно занулить
Умножаем первую строку на 3 и складываем со второй
![]()
![]()
Результат запишем вместо второй строки.
Умножаем первую строку на 2 и вычитаем из результата третью строку
![]()
![]()
Результат запишем вместо третьей строки. Умножаем первую строку на 2 и вычитаем из результата четвертую строку
![]()
![]()
Результат записываем вместо четвертой строки

Первый ненулевой элемент во второй строке указан и обведены элементы подлежащие занулению. Какие элементарные преобразования нужно сделать для зануления требуемых элементов? После преобразований получаем эквивалентную матрицу

В эквивалентной системе

Получили противоречивое равенство. Поэтому система несовместна.
Ответ: система несовместна.
Задача 3. Решить систему методом Гаусса

Решение: Запишем расширенную матрицу системы

Здесь уже указан первый ненулевой первой строки и обведены элементы под ним, которые нужно занулить. Для зануления требуемых элементов выполнить действия:
Из первой строки вычесть две вторые строки. Результат записать вместо второй строки.
Первую строку умножить на 3 и из результата вычесть две третьи строки. Результат записать вместо третьей строки.
Из первой строки вычесть две четвертые строки. Результат записать вместо четвертой строки.
Результат всех действий

Здесь указан первый ненулевой элемент второй строки и обведены элементы под ним, которые нужно занулить. Схематически указаны требуемые действия:
Вторую строку умножаем на 13 и из результата вычитаем девять третьих строк.
Вторую строку складываем с тремя четвертыми строками.
Результат действий

Нулевую строку вычеркиваем. Вторую строку можно разделить на 3.
Результат действий

Первые ненулевые
находятся в первом, третьем и пятом
столбце. Поэтому
![]() ,
,
,
,
![]() –зависимые переменные, остальные
–зависимые переменные, остальные
![]() ,
,
![]() – независимые переменные. Запишем
эквивалентную систему
– независимые переменные. Запишем
эквивалентную систему

Независимые переменные переносим в правые части уравнений

Поднимаемся от последнего уравнения к первому
1)
![]()
2)
![]()
![]()
![]() ,
,
![]()
3)
![]()
![]()
![]()
![]()
Ответ:

![]() ,
,
![]() .
.
Для самостоятельного решения:
1. Решить систему линейных уравнений методом Крамера, Гаусса и матричным способом.
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

11.
 12.
12.

13.
 14.
14.

15.
 16.
16.

17.
 18.
18.
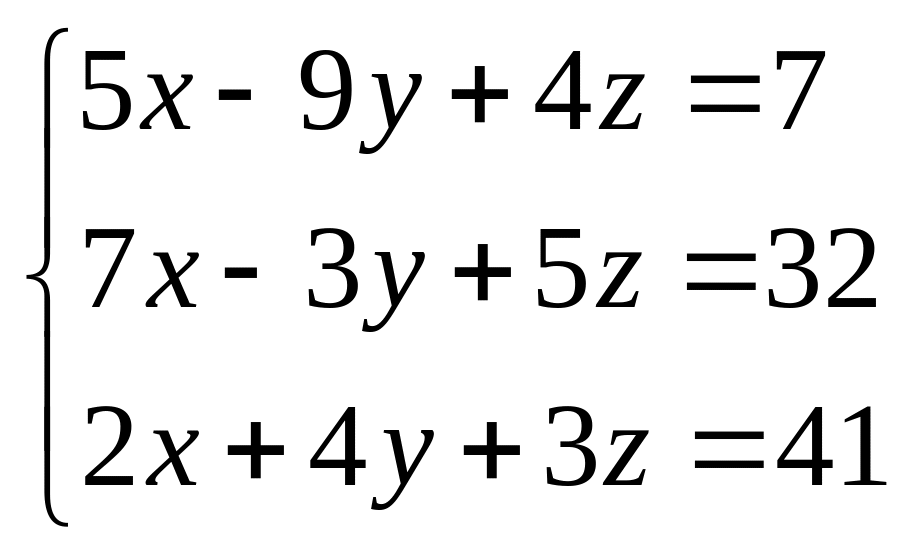
19.
 20.
20.

2. Решить систему линейных уравнений методом Гаусса
1.
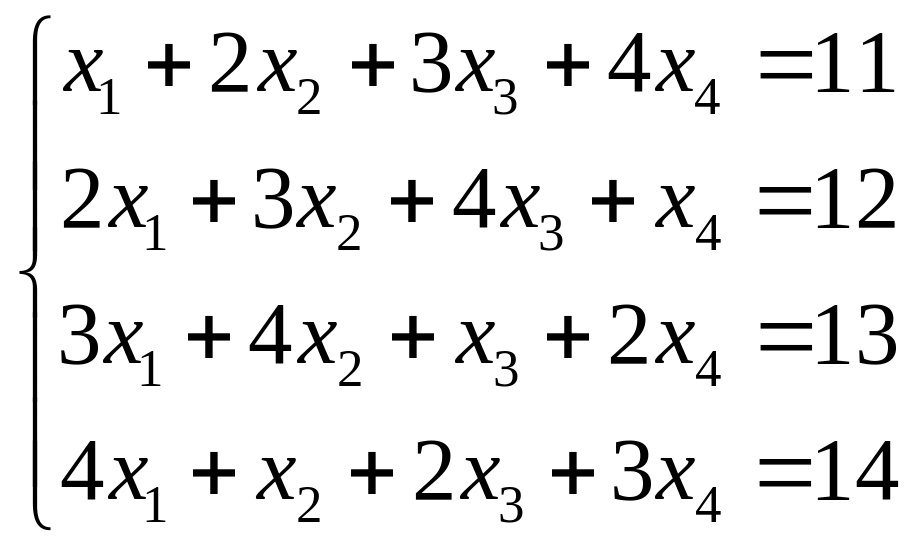 2.
2.
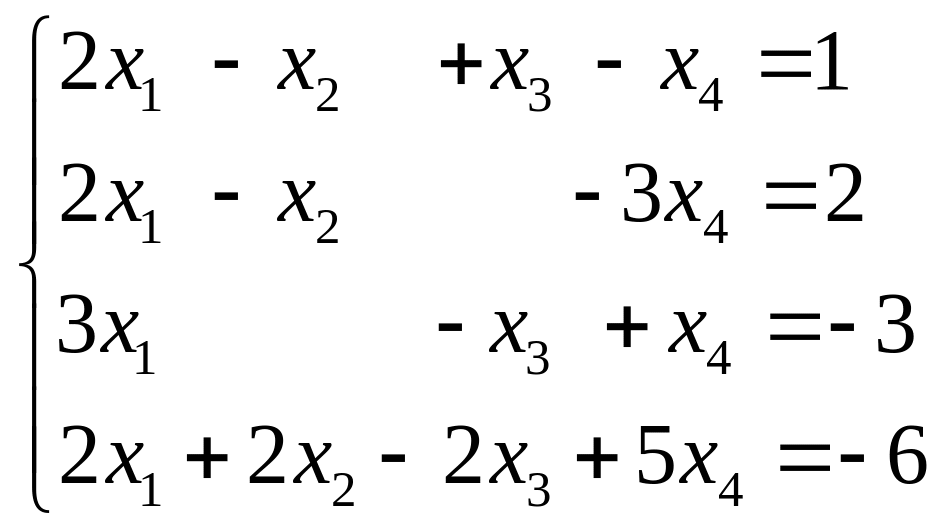
3.
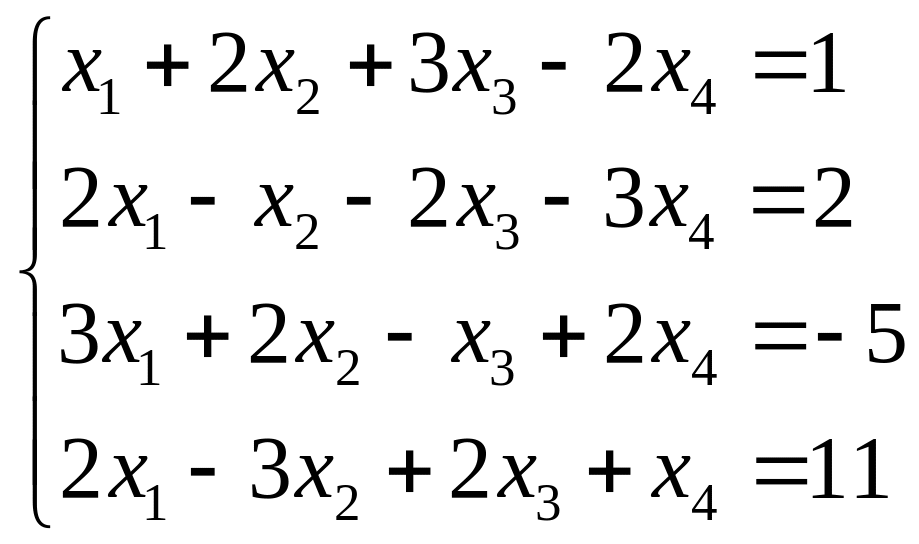 4.
4.

5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

11.
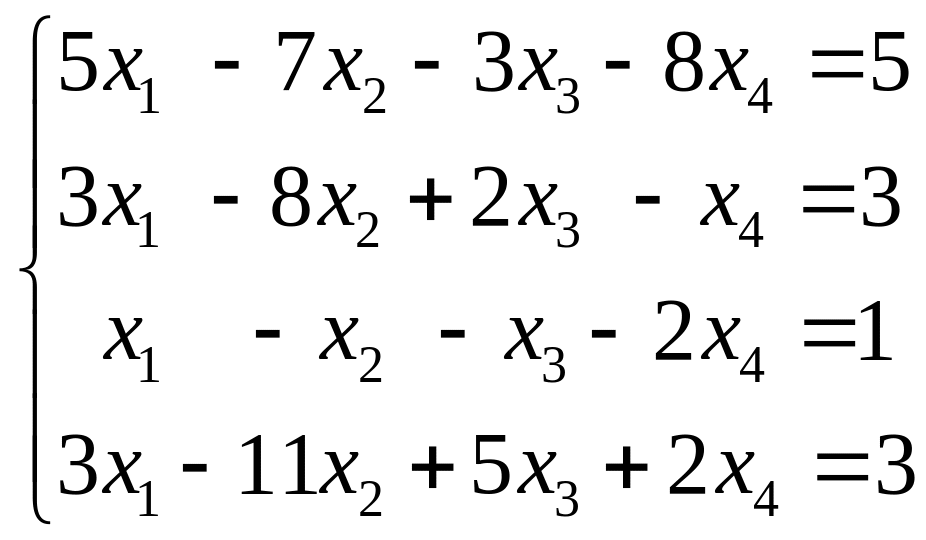 12.
12.

13.
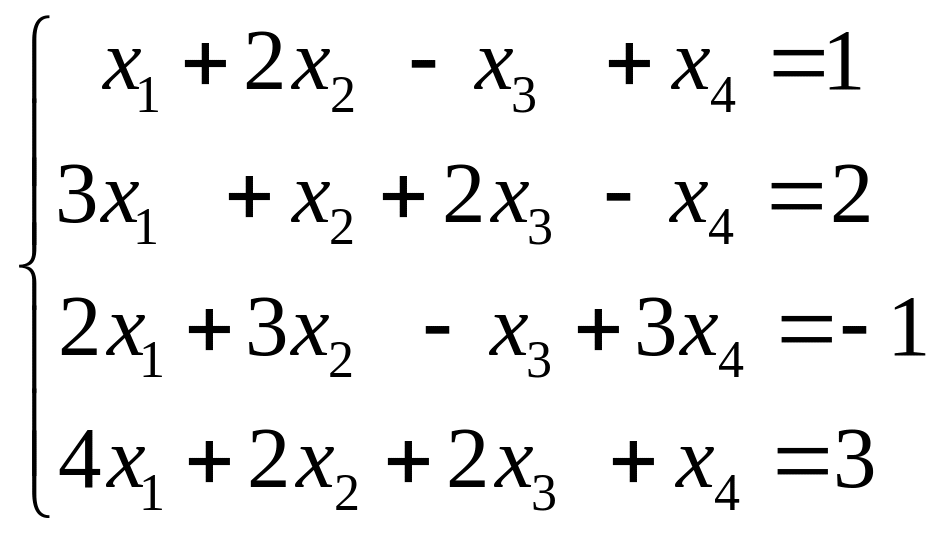 14.
14.

15.
 16.
16.

17.
 18.
18.

19.
 20.
20.

