2.2. Умножение матрицы на число
Матрицу любой
размерности можно умножить на число
.
Это значит – умножить на число все
элементы матрицы:
,
т.е.
если
,
то
.
Примеры выполнения заданий:
Задача 1. Даны
матрицы:
.
Выполните действия:
.
Решение:
;
.
Ответ:
.
Задача 2. Найдите
значение линейной комбинации матриц
.
Решение:
.
Ответ:
.
Для самостоятельного решения:
Найдите линейные комбинации заданных матриц:
1)
.
2)
.
3)
.
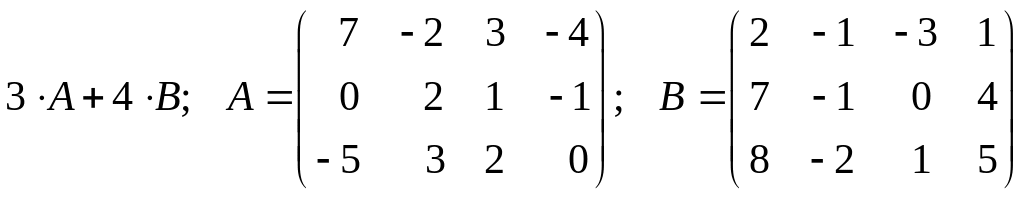2.3. Умножение матриц
Матрицу A можно умножить на матрицу B только в том случае, когда число столбцов матрицы A равно числу строк матрицы B.
В результате
умножения получится матрица C,
у которой столько же строк, сколько их
в матрице A, и столько
же столбцов, сколько их в матрице B,
а элементы матрицы C
вычисляются по формуле:
.
Другими словами:
для получения элемента
,
расположенного в i-ой
строке и j-ом столбце
матрицы C надо элементы
i-ой строки матрицы A
умножить на соответствующие элементы
j-го столбца матрицы
B и полученные
произведения сложить.
Алгоритм вычисления произведения матрицы на матрицу :
1) Проверить,
совпадает ли число столбцов матрицы
с числом строк матрицы
,
(«согласованы» ли порядки множителей).
Только в этом случае можно умножить A
на B. В противном случае
вычислить C нельзя.
2) Определить
порядок матрицы произведения:
имеет
порядок
,
где
m – число строк первого
множителя A, k
– число столбцов второго множителя B.
3) Вычислить каждый
элемент матрицы произведения C
по формулам:
4) Выписать полученную матрицу C.
Примеры выполнения заданий:
Задача 1. Найдите
произведение матриц
,
если
.
Решение:
1. Проверим, совпадает ли число столбцов матрицы А с числом строк матрицы B – совпадают, порядки множителей «согласованы».
2. Определим порядок
матрицы произведения:
имеет порядок
,
где 2 – число строк первого множителя
A, 2 – число столбцов
второго множителя B.
3. Вычислим каждый элемент матрицы произведения C по формулам:
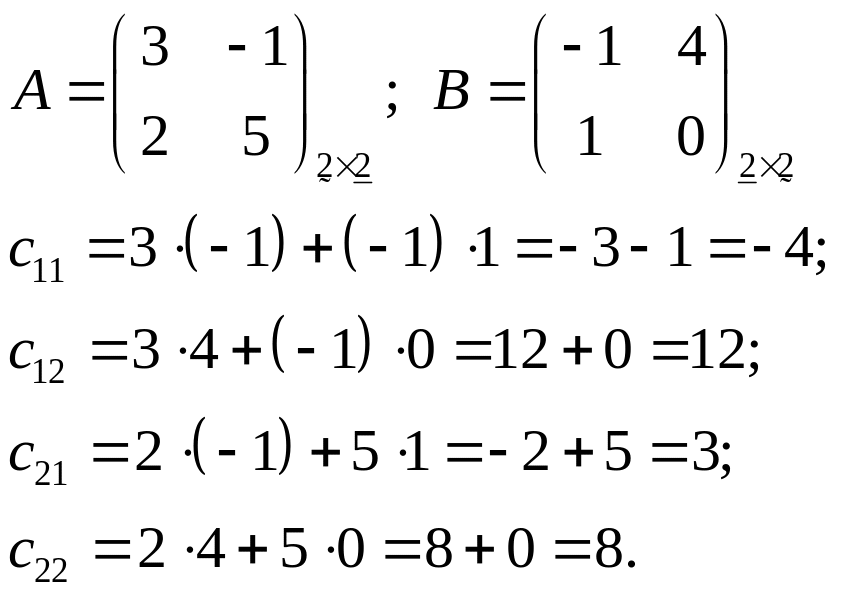
4. Выписать полученную матрицу C.
Ответ:
.
Задача 2. Пусть
.
Найдите произведения
и
(если это возможно).
Решение:
Произведение
не существует, так как число столбцов
матрицы B не совпадает
с числом строк матрицы
.
Задача 3. Найдите
произведение матриц
,
если
;
Решение:
.
Ответ:
.
Задача 4. Найдите
произведение матриц
,
если
.
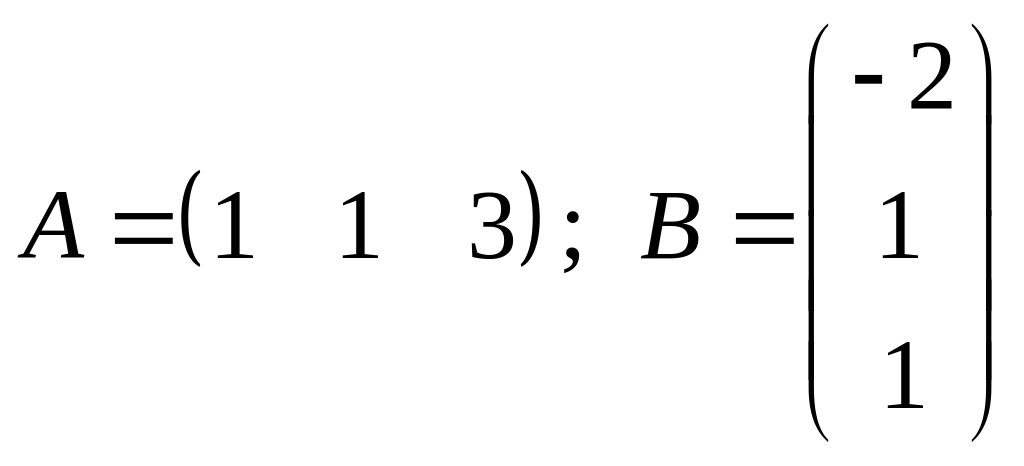Решение:
.
Ответ: 2.
Задача 5. Найдите
произведение матриц
,
если
.
Решение:
.
Ответ:
.
Задача 6. Найдите
произведение матриц
,
если
.
Решение:
.
Ответ:
.
Задача 7.
Найдите произведение матриц
,
если
Решение:
.
Ответ:
.
Задача 8. Найдите
произведение матриц
,
если
.
Решение:
Ответ:
.
Для самостоятельного решения:
Даны матрицы
.
Найти
и
.
Докажите, что
.
Свойства операции умножения матриц
1. Умножение
матриц не коммутативно, т.е.
,
даже если определены оба произведения.
Однако если для каких-либо матриц
соотношение
выполняется, то такие матрицы называются
еще перестановочными.
Самым характерным
примером может служить единичная матрица
E, которая является
перестановочной с любой другой матрицей
того же размера. Перестановочными могут
быть только квадратные матрицы одного
и того же порядка
.
Очевидно, что для любых матриц выполняется
следующее свойство:
,
где O – нулевая
матрица.
2. Операция
перемножения матриц ассоциативна,
т.е. если определены произведения
и
,
то определены
и
,
и выполняется равенство:
.
3. Операция умножения
матриц дистрибутивна по отношению
к сложению, т.е. если имеют смысл выражения
и
,
то соответственно:
4. Если произведение
определено, то для любого числа k
верно соотношение:
.
Замечание 1.1. Произведение матриц определено только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведение матриц содержит столько строк, сколько имеет первая матрица, и столько столбцов, сколько имеет вторая матрица.
Замечание 1.2. В общем случае , даже если оба произведения матриц, и , определены. Матрицы, для которых выполняется условие , называются коммутативными.
5. Как и умножение чисел, произведение матриц подчиняется сочетательному закону: .
Для самостоятельного решения:
Проверьте, коммутируют ли матрицы
1.
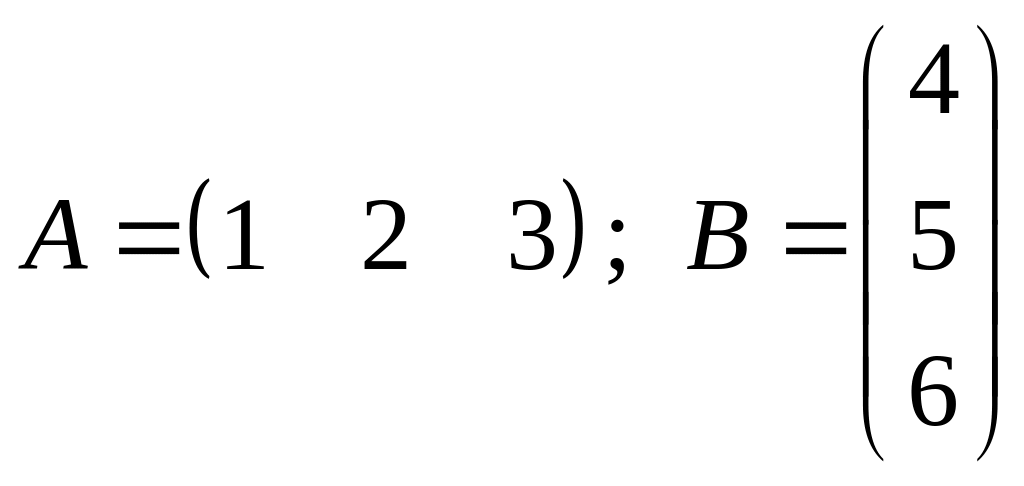; 2.
;
3.
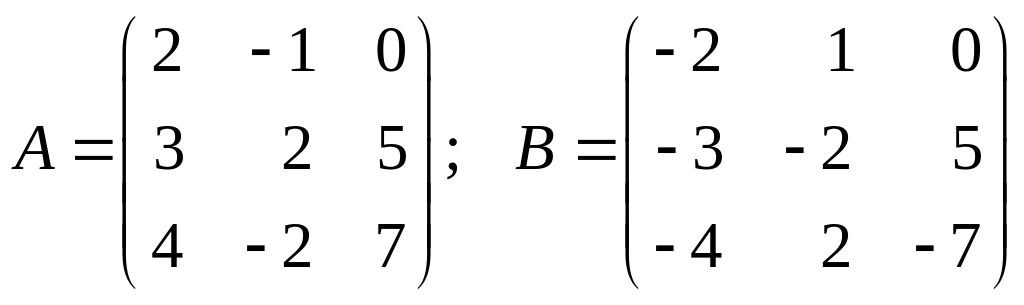; 4.
.