
- •Ряды Числовые ряды. Признаки сходимости.
- •1. Понятие числового ряда
- •2. Сходимость и расходимость числового ряда
- •3. Понятие суммы ряда
- •4. Примеры сходящихся и расходящихся рядов
- •5. Необходимый признак сходимости ряда
- •6. Достаточный признак расходимости ряда
- •7. Остаток ряда
- •8. Некоторые операции над рядами
- •Умножение ряда на число.
- •Сумма (разность) двух рядов.
- •3) Группировка членов ряда.
- •9. Числовые ряды с положительными членами
- •10. Перестановка членов ряда
- •11. Достаточные признаки сходимости рядов с положительными членами
- •Признак сравнения.
- •Признак Даламбера.
- •Признак Коши
- •Интегральный признак Маклорена-Коши
- •Пример14. Ряд расходится. Пример 15. Ряд сходится.
- •12. Ряды со знакочередующимися членами
- •13. Ряды с произвольными членами
Интегральный признак Маклорена-Коши
Теорема
13.
Пусть дан ряд с положительными членами
(15) и существует функция
![]() такая, что
такая, что
![]()
При этом функция
![]() непрерывна в промежутке
непрерывна в промежутке
![]() положительна, и убывает в этом промежутке.
Тогда, если интеграл
положительна, и убывает в этом промежутке.
Тогда, если интеграл
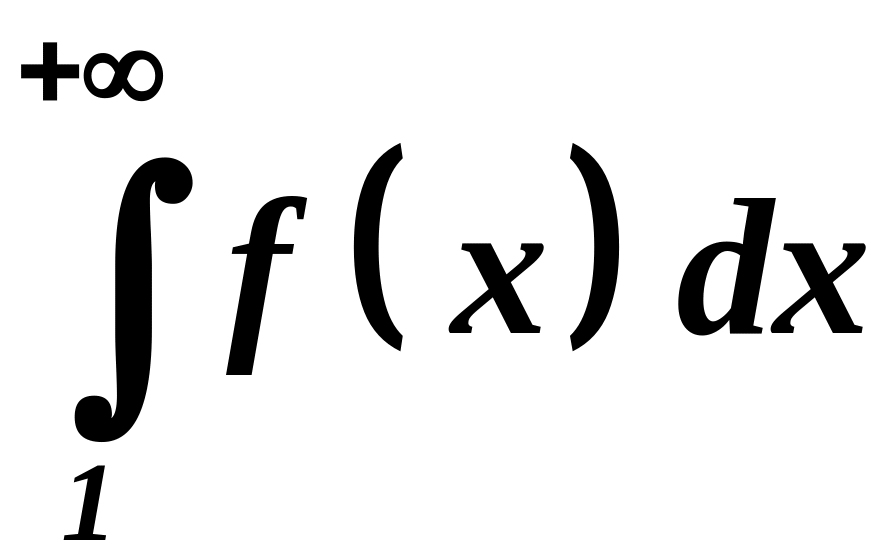 сходится, то и ряд (1) сходится, а если
интеграл
расходится, то и ряд (15) расходится.
сходится, то и ряд (1) сходится, а если
интеграл
расходится, то и ряд (15) расходится.
Пример
13.
Исследовать на сходимость обобщенный
гармонический ряд:
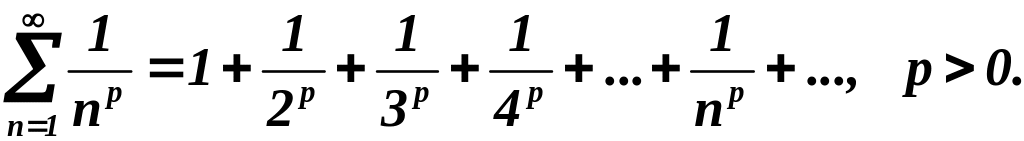
Решение.
При
![]() имеем ряд:
имеем ряд: 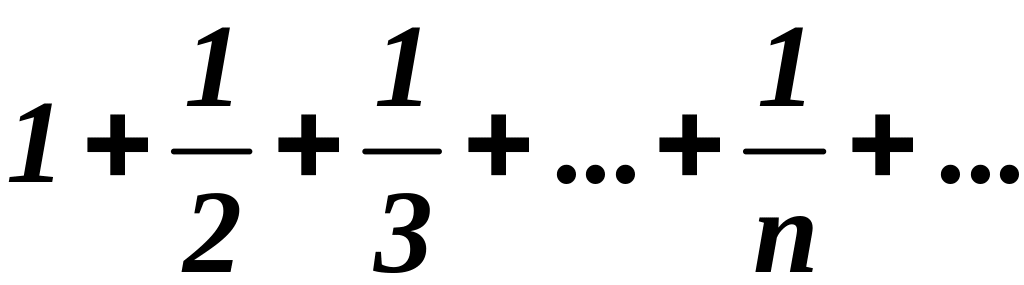 .
Это гармонический ряд, и он расходится.
.
Это гармонический ряд, и он расходится.
Пусть
![]() Рассмотрим функцию:
Рассмотрим функцию:
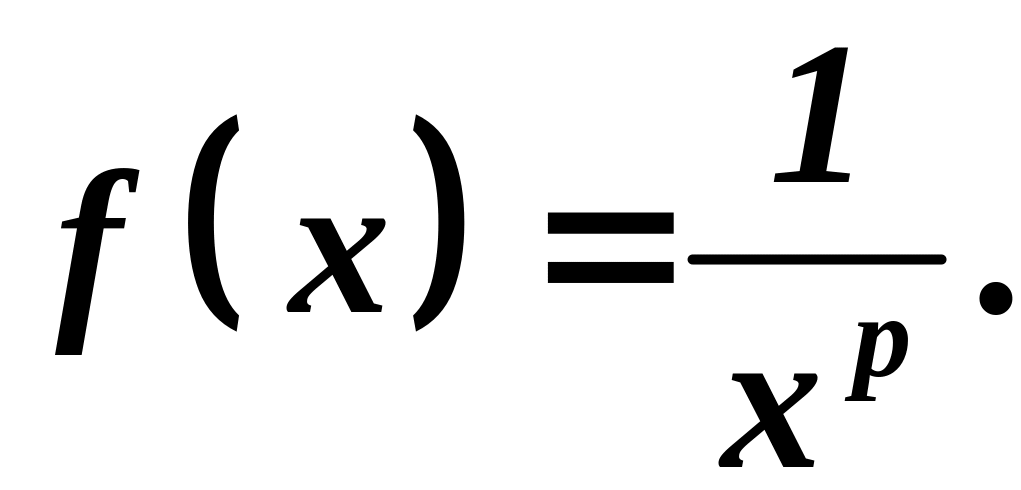 Нетрудно проверить, что
удовлетворяет всем условиям теоремы:
Нетрудно проверить, что
удовлетворяет всем условиям теоремы:
![]()
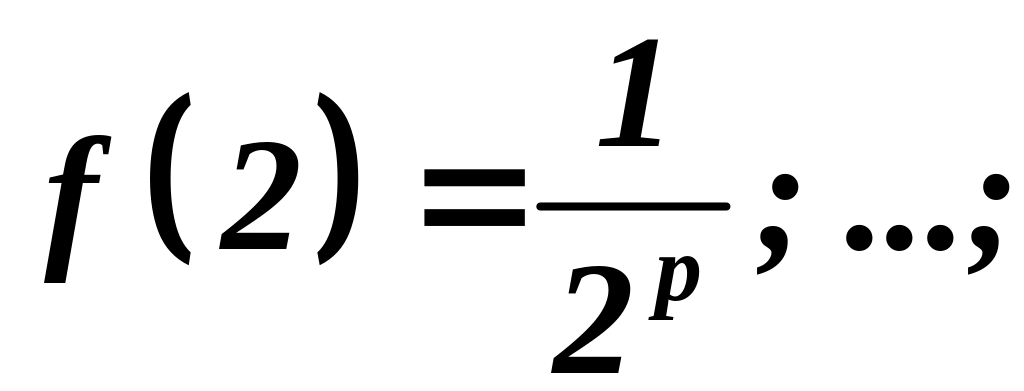
 .
Эта функция непрерывна в промежутке
положительна, и строго убывает.
.
Эта функция непрерывна в промежутке
положительна, и строго убывает.
Рассмотрим интеграл:
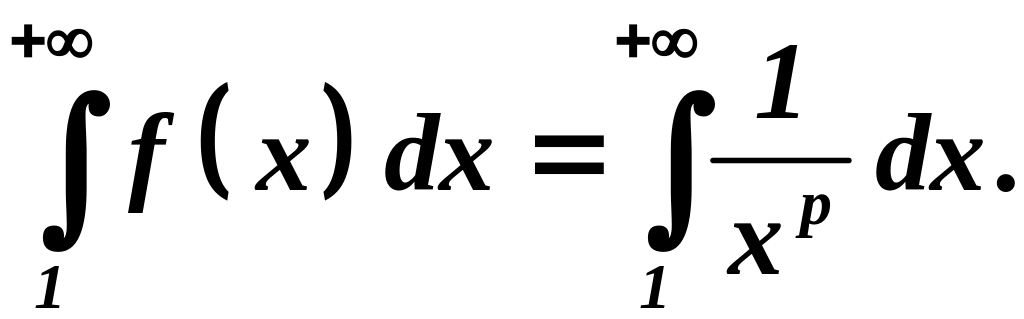
Из интегрального
исчисления известно, что этот интеграл
сходится при
![]() и расходится при
и расходится при
![]() значит, утверждаем, что обобщенный
гармонический ряд сходится при
и расходится при
значит, утверждаем, что обобщенный
гармонический ряд сходится при
и расходится при
![]()
Пример14. Ряд расходится. Пример 15. Ряд сходится.
12. Ряды со знакочередующимися членами
Определение 4. Рядами со знакочередующимися членами называются ряды вида:
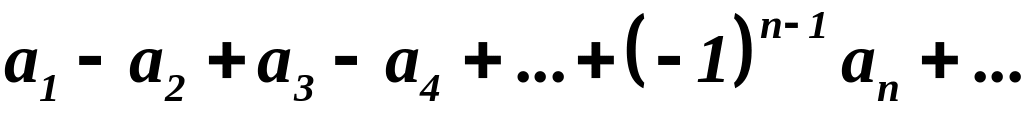 ;
;
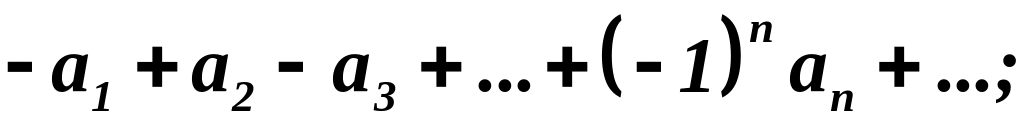
при любом п.
Так как второй
ряд получается из первого умножением
на
![]() то можно изучать первый ряд и все будет
справедливо для второго ряда. Для
знакочередующихся рядов имеет место
теорема, которая является достаточным
признаком сходимости ряда.
то можно изучать первый ряд и все будет
справедливо для второго ряда. Для
знакочередующихся рядов имеет место
теорема, которая является достаточным
признаком сходимости ряда.
Теорема Лейбница 14. Если в ряде (18)
Члены убывают по
модулю, т.е.
![]() при любом п
и предел
при любом п
и предел
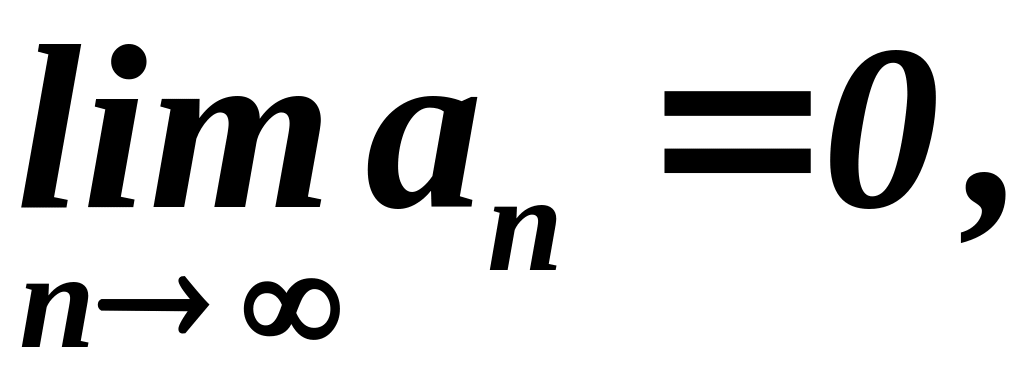 то ряд сходится.
то ряд сходится.
Доказательство. Пусть для ряда (18) условия теоремы выполняются. Рассмотрим частичную сумму ряда с четным номером 2п:
![]()
Перепишем ее в
виде:
![]() (19)
(19)
В формуле (19) каждая
скобка справа будет больше нуля, т.к.
![]() поэтому
поэтому
![]() при любом п.
Кроме этого, очевидно, что последовательность
будет строго возрастать. Покажем, что
эта последовательность является
ограниченной сверху. Перепишем
при любом п.
Кроме этого, очевидно, что последовательность
будет строго возрастать. Покажем, что
эта последовательность является
ограниченной сверху. Перепишем
![]()
![]() (20)
(20)
Так как
![]() то
то
![]() значит, из (20) следует, что
значит, из (20) следует, что
![]() Таким образом,
Таким образом,
![]() будучи строго возрастающей, ограничена
сверху числом
будучи строго возрастающей, ограничена
сверху числом
![]() .
Тогда по теореме Вейерштрасса утверждаем,
что последовательность
имеет конечный предел, обозначим его
S:
.
Тогда по теореме Вейерштрасса утверждаем,
что последовательность
имеет конечный предел, обозначим его
S:
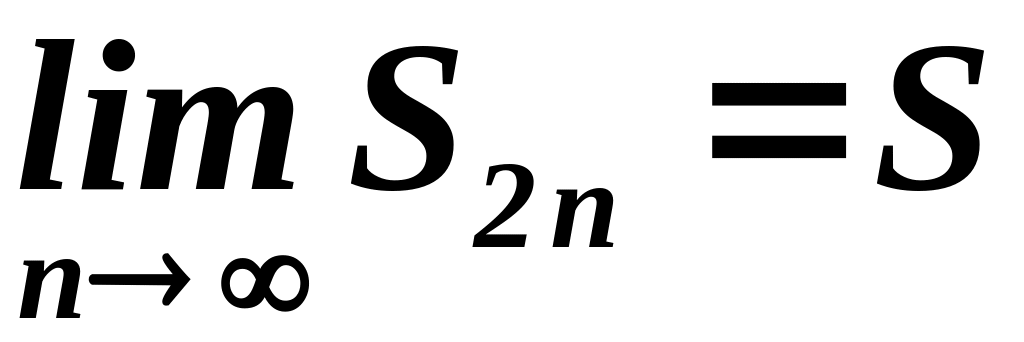 .
.
Рассмотрим последовательность частичных сумм с нечетными номерами . Запишем равенство:
![]()
![]() (21)
(21)
Так как по условию
теоремы
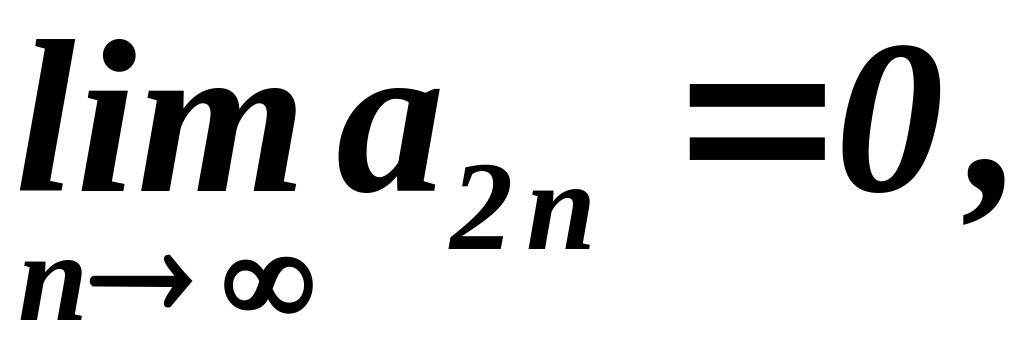 то, переходя к пределу в равенстве (21),
получим:
то, переходя к пределу в равенстве (21),
получим:
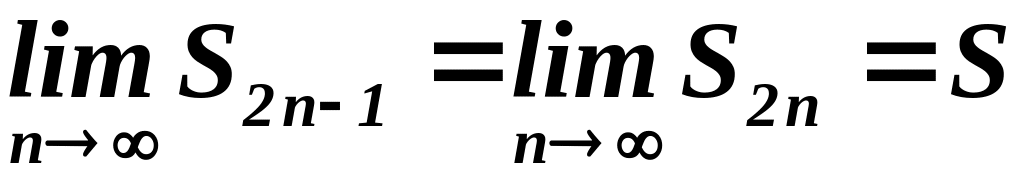
Итак,
последовательности частичных сумм с
четными и нечетными номерами имеют один
и тот же предел S.
Отсюда следует, что последовательность
частичных сумм ряда (18)
имеет предел, равный S.
В самом деле, возьмем произвольное
![]() и рассмотрим окрестность точки S.
Так как
,
то в
и рассмотрим окрестность точки S.
Так как
,
то в
![]() -окрестности
точки S
будут
находится все члены последовательности
,
начиная с некоторого номера. Так как
-окрестности
точки S
будут
находится все члены последовательности
,
начиная с некоторого номера. Так как
 ,
то в этой же окрестности будут находиться
все члены последовательности, начиная
с некоторого номера. Следовательно,
можно указать номер, с которого все
члены последовательности
и с четными, и с нечетными номерами будут
находиться в некоторой окрестности
точки S,
то есть
,
то в этой же окрестности будут находиться
все члены последовательности, начиная
с некоторого номера. Следовательно,
можно указать номер, с которого все
члены последовательности
и с четными, и с нечетными номерами будут
находиться в некоторой окрестности
точки S,
то есть
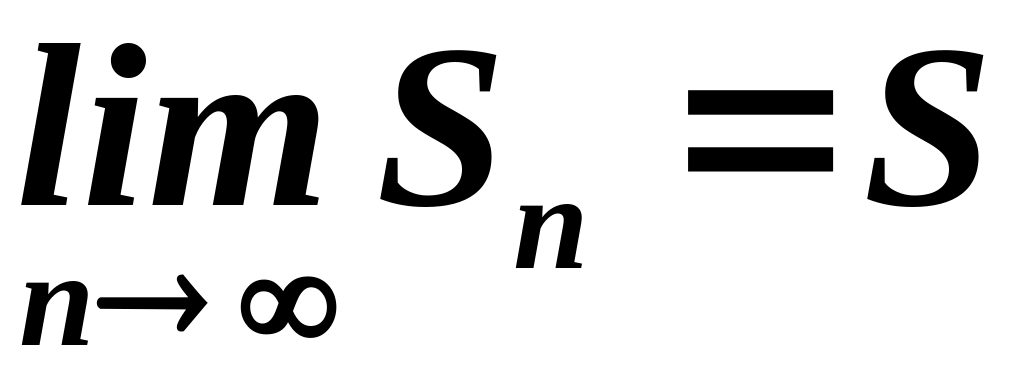 .
Теорема доказана.
.
Теорема доказана.
Определение 5. Ряды со знакочередующимися членами, которые удовлетворяют условиям теоремы Лейбница, называются рядами лейбницкого типа.
Следствие
3(из теоремы Лейбница). Если
S
– сумма ряда
лейбницкого типа, то модуль
![]() .
Это следствие имеет значение в приближенных
вычислениях суммы ряда.
.
Это следствие имеет значение в приближенных
вычислениях суммы ряда.
