13. Ряды с произвольными членами
Определение 6. Числовой ряд (22)
называется рядом с произвольными членами, если в нем имеется бесконечное множество положительных членов и бесконечное множество отрицательных членов.
Частным видом ряда с произвольными членами является ряд со знакочередующимися членами.
Определение
7. Числовой
ряд (22) называется абсолютно
сходящимся,
если сходится ряд, составленный из
модулей членов этого ряда:
(23)
Пусть ряд (22) сходится абсолютно, это значит, по определению, что сходится ряд (23). Возникает вопрос, а сходится ли сам ряд (22)? Ответ дает теорема.
Теорема 15. Абсолютно сходящийся ряд есть ряд сходящийся.
Определение 8. Числовой ряд (22) называется не абсолютно сходящимся, если он сходится, а ряд, составленный из модулей его членов, т.е. ряд (23) расходится. Не абсолютно сходящийся ряд называется условно сходящимся.
Пример
16.
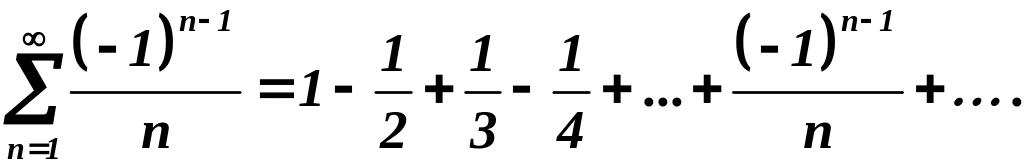
Решение.
Этот ряд со знакочередующимися членами,
его члены убывают по модулю, и
.
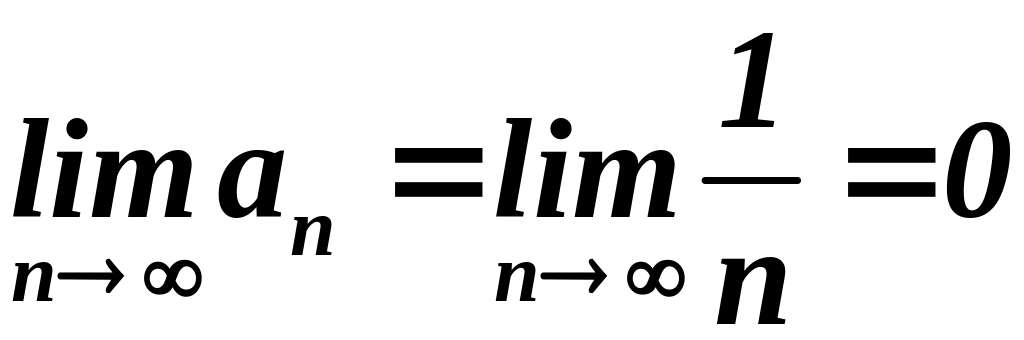Ряд сходится по теореме Лейбница. Запишем
ряд, состоящий из модулей:
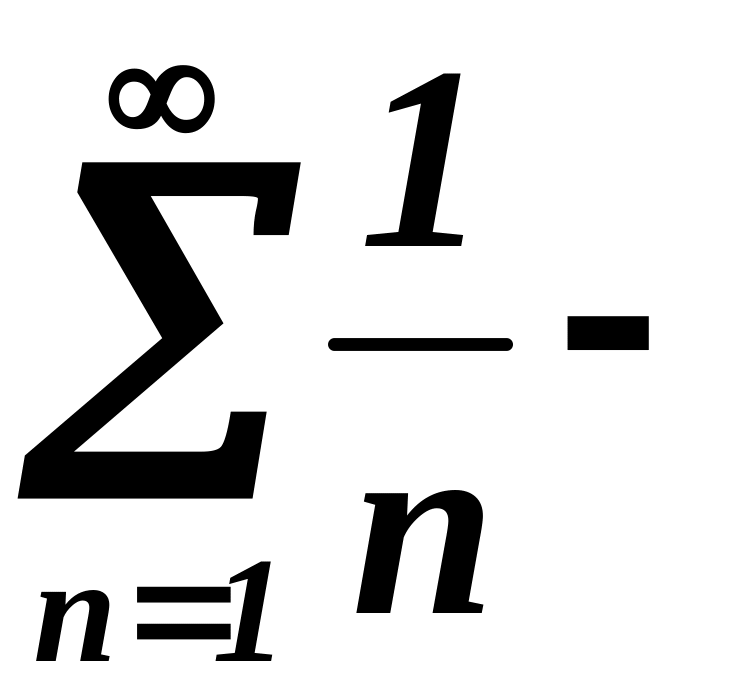гармонический
ряд. Он расходится. Следовательно,
исходный ряд сходится условно.
Пример
17.
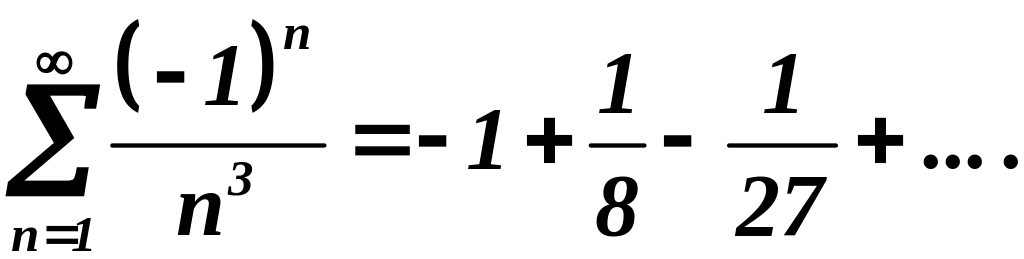
Решение.
Этот ряд со знакочередующимися членами.
Он сходится по теореме Лейбница. Запишем
ряд, состоящий из модулей:
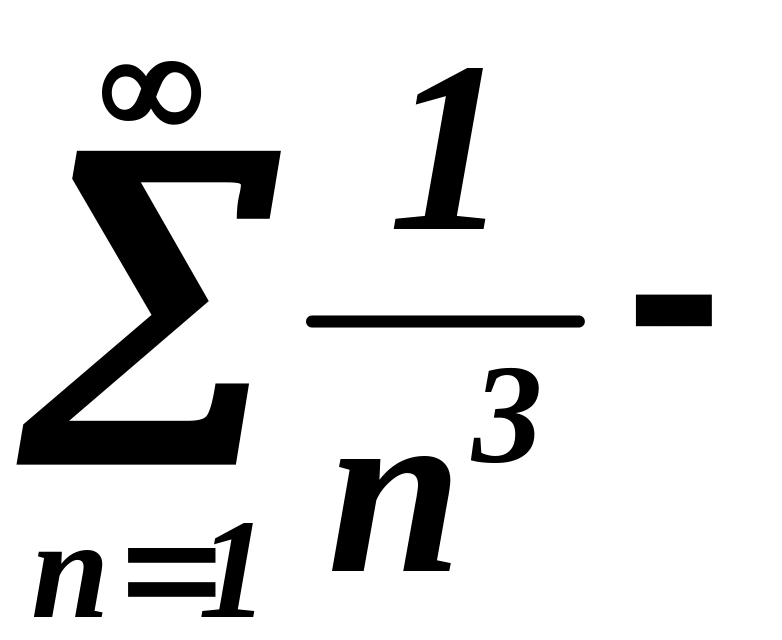обобщенный гармонический ряд. Он сходится
при
Значит, исходный ряд сходится абсолютно.
14. Достаточные признаки сходимости рядов с произвольными членами
Признак сравнения
Теорема 16. Пусть дан ряд с произвольными членами
(25)
и сходящий ряд с положительными членами
Если хотя бы, начиная с некоторого номера, выполняется неравенство:
то ряд (24) сходится и при том абсолютно.
Признак Даламбера
Теорема 17. Если ряд (26)
таков, что существует
предел
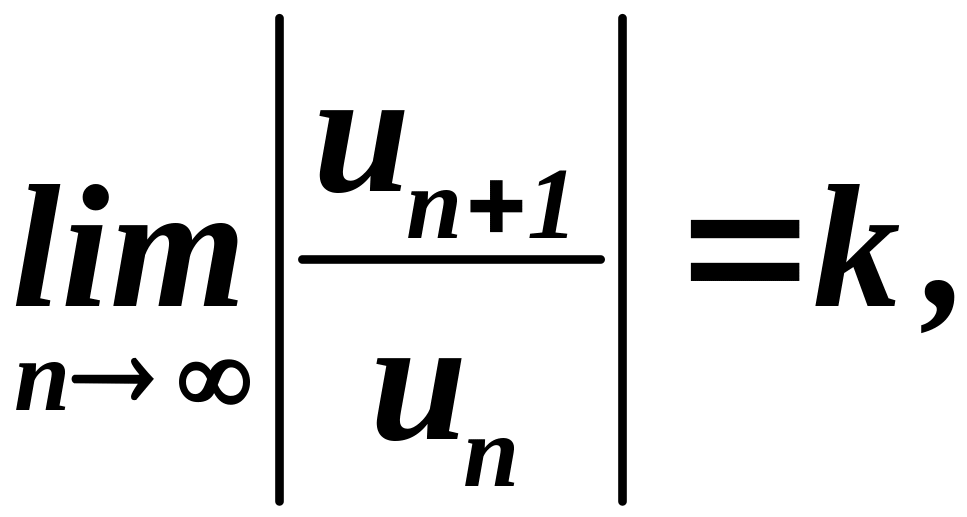то при
ряд (26) сходится и при том абсолютно, при
ряд (26) расходится. При
признак Даламбера не дает ответа на
вопрос о сходимости или расходимости
ряда.
Признак Коши
Теорема
18.
Если числовой ряд
(27) таков, что существует предел
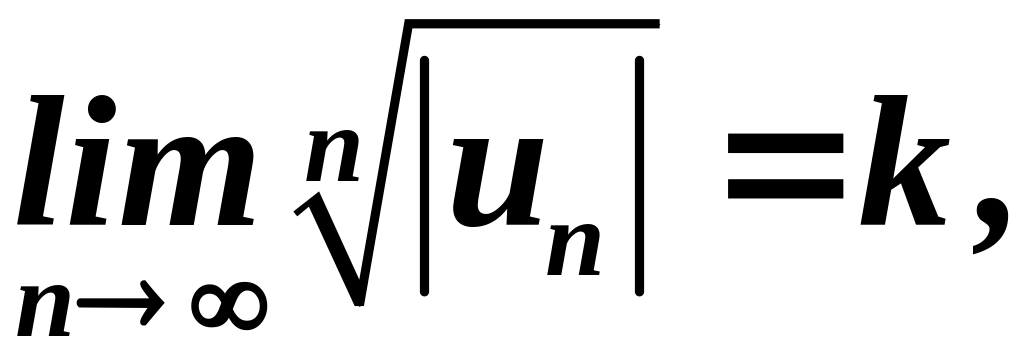то при
ряд (27) сходится и при том абсолютно, при
ряд (27) расходится. При
признак Коши не дает ответа на вопрос
о сходимости или расходимости ряда.
15. Перестановка членов ряда
Теорема 19. Если члены абсолютно сходящегося ряда переставить каким-либо образом, то получим ряд, который абсолютно сходится, и его сумма равна сумме исходного ряда.
Эта теорема выражает переместительное свойство абсолютно сходящихся рядов. Для условно сходящихся рядов переместительное свойство не справедливо. Более того, имеет место следующая теорема.
Теорема 20. (теорема Римана). Если ряд сходится не абсолютно, то переставляя его члены, можно добиться того, что вновь полученный ряд будет иметь любую наперед заданную сумму.
В частности, переставляя члены ряда, можно добиться расходимости вновь полученного ряда.