Ряды Числовые ряды. Признаки сходимости.

1. Понятие числового ряда

Пусть дана бесконечная последовательность действительных чисел:

Соединяя члены последовательности знаками (+), получим символ: (1)

Этот символ носит название числового ряда. Кратко числовой ряд (1) записывают: Числа, образующие числовой ряд (1), называются его членами: первый член ряда, второй член ряда и т.д., называется общим членом ряда.

Пример 1. Пусть числовой ряд. Общий член этого ряда равен п.

Пример 2. Дан числовой ряд: . п-ый член ряда равен:

Пример 3. Гармонический ряд: Запишем общий член ряда:

Пример 4. Ряд геометрической прогрессии: Запишем общий член ряда:

Замечание 1. Не всегда общий член ряда определяется формулой. Например, рассмотрим ряд, членами которого являются все последовательные простые числа: . Так как не существует формулы, по которой можно написать любое простое число на заданном месте, то общий член ряда не может быть выражен аналитически.

2. Сходимость и расходимость числового ряда

Пусть дан числовой ряд: (2)

В определении ряда сказано, что это символ. Однако этот символ имеет реальный смысл. Он имеет (правда не всегда) конкретное числовое значение. Обозначим через через сумму двух первых членов ряда (2), т.е. через и т.д.,

Число называется первой частичной суммой ряда (2), число второй частичной суммой ряда (2), число -ой частичной суммой ряда (2).

Запишем последовательность частичных сумм Это числовая последовательность, так как при любом п - есть действительное число, но тогда могут представиться три случая:

1. последовательность частичных сумм ряда (2) имеет конечный предел;

2. последовательность частичных сумм ряда (2) имеет бесконечный предел;

3. последовательность частичных сумм ряда (2) не имеет предела.

Определение 1. Числовой ряд

называется сходящимся, если последовательность его частичных сумм имеет конечный предел.

Определение 2. Числовой ряд

называется расходящимся, если последовательность его частичных сумм имеет бесконечный предел или не имеет предела.

3. Понятие суммы ряда

Пусть числовой ряд (3)

сходится. Это значит, по определению, что последовательность его частичных сумм имеет конечный предел. Обозначим его через S:

Число S называется суммой ряда (3). Можно записать: .

4. Примеры сходящихся и расходящихся рядов

Пример 5. Пусть дан ряд:

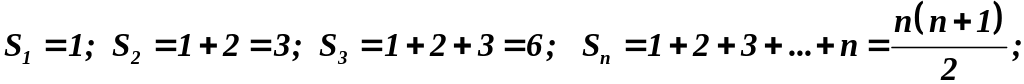
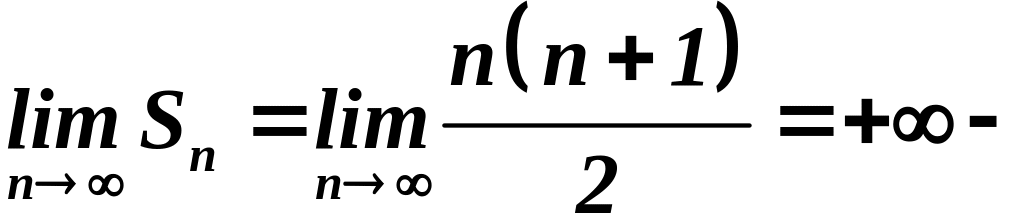ряд расходится.

Пример 6. Имеем ряд:

Не трудно проверить, что

Ряд сходится и его сумма равна 1.

Пример 7. Дан гармонический ряд:

Запишем п-ю частичную сумму:

Докажем, что гармонический ряд расходится. Из теории пределов известно, что последовательность с общим членом имеет конечный предел, равный е. (Второй замечательный предел).

При этом известно, что эта последовательность строго возрастает, значит, при любом п имеем:

Запишем неравенство при

Складывая почленно неравенства, получим:

Переходя к пределу при получим:

Значит, Гармонический ряд расходится.

Пример 8. Исследовать на сходимость ряд: (4)

п- ая частичная сумма есть сумма первых п членов геометрической прогрессии и, как известно, Рассмотрим случаи:

1. Пусть тогда Значит,

Ряд сходится и его сумма равна

2. Пусть тогда (в зависимости от а).

Ряд расходится.

3. Пусть тогда не существует. Ряд расходится.

4. Пусть тогда .

(в зависимости от а). Ряд расходится.

5. Пусть тогда . Последовательность частичных сумм предела не имеет, т.к.

Итак, если то ряд (4) сходится; если то ряд (4) расходится.