1.5. Шифрування методом гамування

1.5.1. Накладання гами шифру на вхідний текст

Під гамуванням розуміють процес накладання за певним законом гами шифру на вхідні дані. Гама шифру – це псевдовипадкова послідовність, створена за заданим алгоритмом для шифрування вхідних даних і дешифрування зашифрованих даних.

Процес шифрування полягає в генеруванні гами шифру і накладанні отриманої гами на початковий вхідний текст у зворотний спосіб, наприклад, з використанням операції додавання за модулем 2.

Необхідно зазначити, що перед шифруванням вхідні дані розбивають на блоки однакової довжини, зазвичай по 64 біти. Гама шифру створюється у вигляді послідовності блоків аналогічної довжини.

Рівняння шифрування можна записати у такому вигляді:

, (4.1)

де  – і-ий блок шифротексту;  – і-ий блок гами шифру;  – і-ий блок вхідного тексту; M – кількість блоків вхідного тексту.

Процес дешифрування зводиться до повторного генерування гами шифру і накладання цієї гами на зашифровані дані. Рівняння дешифрування має такий вигляд

, (4.2)

Отриманий цим методом шифротекст є надто складним для розкриття, оскільки тепер ключ є постійно змінним. По суті, гама шифру має змінюватися випадково для кожного зашифровуваного блока. Якщо період гами перевищує довжину всього зашифровуваного тексту і зловмисникові невідома жодна з частин вхідного тексту, то такий шифр можна розкрити тільки безпосереднім перебиранням усіх варіантів ключа. У цьому випадку криптостійкість шифру визначається довжиною ключа.

1.5.2. Методи генерування псевдовипадкових послідовностей чисел

При шифруванні методом гамування як ключ використовується випадковий рядок бітів, котрий поєднується з вхідним текстом, також поданим у двійковому вигляді (наприклад, m = 00010, Г = 00011, Ш = 00001 і т.д.), за допомогою побітового додавання за модулем 2 – і внаслідок виконання таких дій виходить зашифрований текст.

Генерування непередбачуваних двійкових послідовностей великої довжини є однією з важливих проблем класичної криптографії. Для розв'язання цієї проблеми широко використовуються генератори двійкових псевдовипадкових послідовностей.

Генеровані псевдовипадкові ряди чисел часто називають гамою шифру, чи просто гамою (за назвою літери  грецького алфавіту, часто використовуваної в математичних формулах для позначання випадкових величин).

Зазвичай, для генерування послідовності псевдовипадкових чисел застосовують комп'ютерні програми, котрі, хоча й називаються генераторами випадкових чисел, насправді видають детерміновані числові послідовності, котрі за своїми властивостями є надто схожі на випадкові.

До криптографічно стійкого генератора псевдовипадкової послідовності чисел (гами шифру) пред'являються три основних вимоги:

• період гами має бути надто великим дня шифрування повідомлень різної довжини;

• гама шифру має бути практично непередбачуваною, що означає неможливість передбачати наступний біт гами, навіть якщо відомі є тип генератора і попередній фрагмент гами;

• генерування гами шифру не повинно призводити до великих технічних складностей.

Довжина періоду гами шифру є найважливішою характеристикою генератора псевдовипадкових чисел. Після закінчення періоду гами шифру числа розпочнуть повторюватися – і їх можна буде передбачати. Необхідна довжина періоду гами шифру визначається ступенем закритості даних. Чим довшим є ключ, тим складніше його підібрати. Довжина періоду гами шифру залежить від обраного алгоритму отримання псевдовипадкових чисел.

Друга вимога пов'язана з такою проблемою: яким способом можна вірогідно переконатися, що псевдовипадкова гама шифру конкретного генератора є насправді непередбачуваною? Поки що не існує таких універсальних і практично перевірених критеріїв і методик. Щоби гама шифру вважалася непередбачуваною, тобто насправді випадковою, необхідно, аби її період був надто великим, а різноманітні комбінації бітів певної довжини були рівномірно розподілені по всій її довжині.

Третя вимога зумовлює можливість практичної реалізації генератора програмно чи апаратно із забезпеченням потрібної швидкодії.

Один з перших способів генерування псевдовипадкових чисел з використанням ЕОМ запропонував у 1946 році Джон фон Нейман. Суть цього способу полягає в тому, що кожне наступне випадкове число утворюється піднесенням до квадрата попереднього числа з відкиданням цифр молодших і старших розрядів. Однак цей спосіб виявився ненадійним – і від нього невдовзі відмовились.

З відомих процедур генерування послідовності псевдовипадкових цілих чисел найчастіше застосовується так званий лінійний конгруентний генератор. Цей генератор продукує послідовність псевдовипадкових чисел ₁, ₂, …, _i-1, _i ,…, використовуючи таке співвідношення:

, (4.3)

де:  – i-те (поточне) число послідовності;  – попереднє число послідовності; a, b та m – константи; m – модуль; а – множник (коефіцієнт); b – приріст. Поточне псевдовипадкове число отримують з попереднього числа множенням його на коефіцієнт a, додаванням з приростом b та обчисленням залишку від ділення на модуль m. Це рівняння генерує псевдовипадкові числа з періодом повторювання, котрий залежить від вибраних значень параметрів a, b та m і може сягати значення m. Значення модуля m обирається таким, щоб дорівнювало 2ⁿ або простому числу, наприклад m = 2³¹ – 1. Приріст b має бути взаємно простим з m, коефіцієнт а має бути непарним числом.

Конгруентні генератори, що працюють за алгоритмом, запропонованим Національним бюро стандартів США, використовуються, зокрема, в системах програмування. Ці генератори мають довжину періоду 2²⁴ і добрі статистичні властивості. Однак така довжина періоду є замалою для криптографічних застосувань. Окрім цього, доведено, що послідовності, згенеровані конгруентними генераторами, не є криптографічно стійкими.

Існує спосіб генерування послідовностей псевдовипадкових чисел з використанням лінійних рекурентних співвідношень. Розглянемо рекурентні співвідношення та їхні різницеві рівняння:

, (4.4)

де: h₀  0, h_k = 1 і кожне h_i належить до поля GF(q).

Розв'язком цих рівнянь є послідовність елеменгів a₀, a₁, a₂, ... поля GF(q). Співвідношення (4.4) визначає правило обчислення a_k за відомими значеннями величин a₀, a₁, a₂, ... a_k-1. Потім за відомими значеннями a₀, a₁, a₂, ..., a_k визначають a_k-1 і т.д. Як наслідок за початковими значеннями a₀, a₁, a₂, ..., a_k-1 можна побудувати нескінченну послідовність, причому кожен її наступний член визначається з k попередніх. Послідовності такого виду легко реалізуються на комп'ютері; при цьому реалізація виходить особливо простою, якщо всі h_i та a_i набувають значень 0 та 1 з поля GF(2).

На рис. 4.1 подано лінійну послідовну перемикальну схему, яку можна використати для обчислення суми (4.4) і, отже, для обчислення значення a_k за значеннями k попередніх членів послідовності. Початкові величини a₀, a₁, a₂, ..., a_k-1 поміщають в розряди зсувного регістру, послідовні зсуву вмісту якого відповідають обчисленню послідовних символів; при цьому вихід i-го зсуву дорівнює a_i. Даний пристрій називають генератором послідовності чисел, який побудовано на базі зсувного регістру з лінійним зворотним зв'язком.

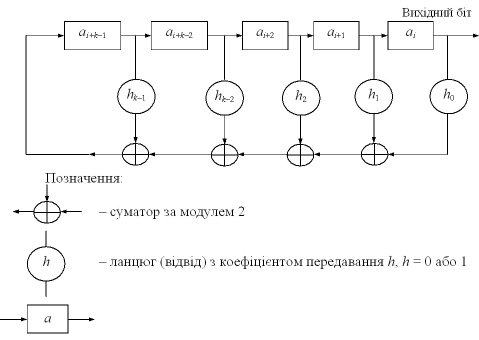
– запам'ятовувальна комірка, котра зберігає a, тобто на виході комірки а = 0 або а = 1

Рис. 4.1. Генератор з регістром зсування

Розв'язки лінійних рекурентних співвідношень, які реалізуються генератором з регістром зсуву, описуються такою теоремою. Нехай многочлен

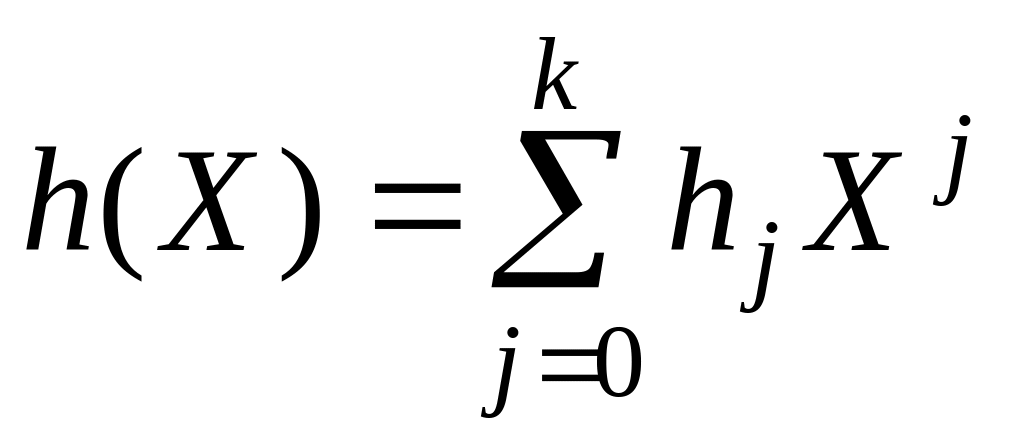, (4.5)

де: X – формальна змінна; h_j – коефіцієнт при X^j, який набуває значення 0 чи 1; h₀  0, h_k = 1, i нехай n – найменше ціле додатне число, для якого многочлен Xⁿ–1 ділиться на h(X). Окрім цього, многочлен

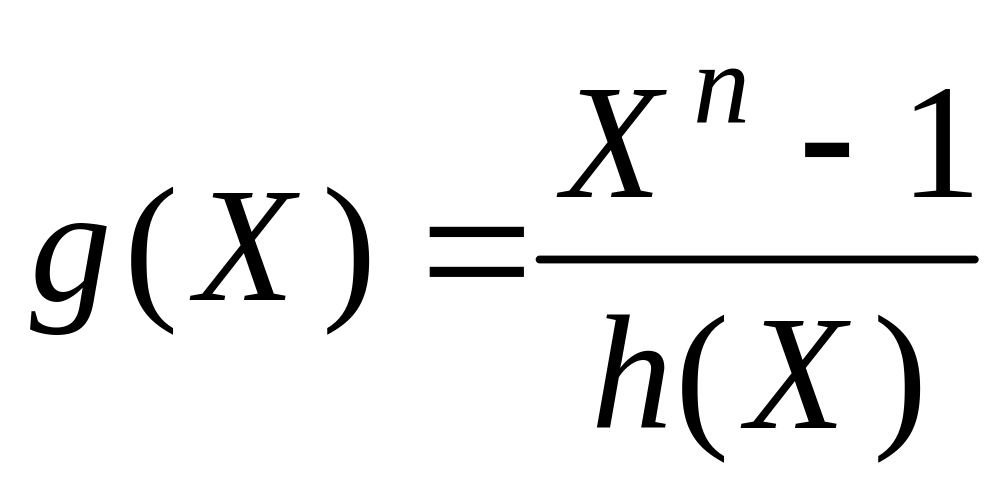, (4.6)

Тоді розв'язки рекурентних співвідношень

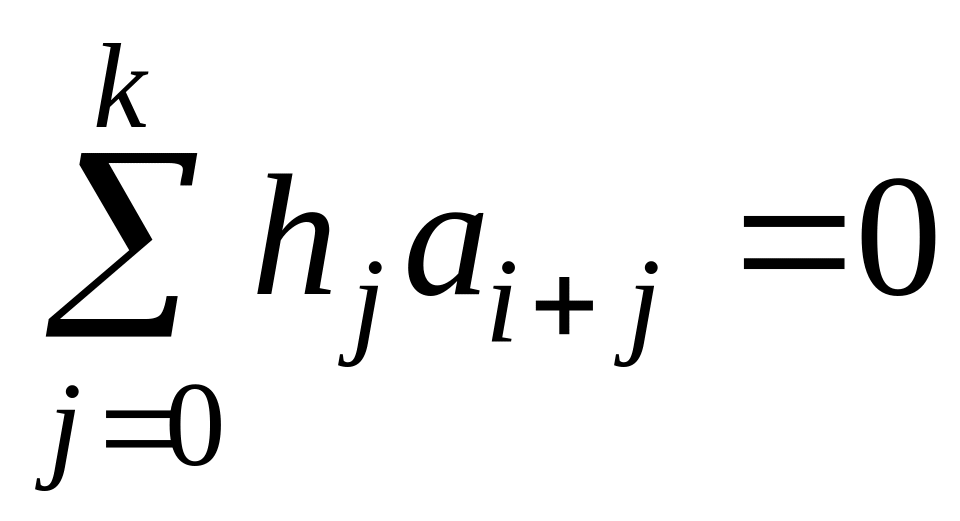(4.7)

у вигляді послідовності елементів a₀, a₁, a₂, ..., a_n-1 є періодичні з періодом n і сукупність, складена з перших періодів усіх можливих розв'язків, яка розглядається як многочлени за модулем (Xⁿ – 1), тобто

(4.8)

збігається з ідеалом, породженим многочленом g(X) в алгебрі многочленів за модулем (Xⁿ – 1).

Зауважимо, що якщо за такого визначення многочлена a(X) елементи а₀, ДІ, а І,… обчислюються в порядку зростання номерів, то коефіцієнти многочлена a(X) обчислюються, розпочинаючи з коефіцієнтів при степенях вищих порядків. Необхідно також зазначити, що вигляд многочлена (4.5) визначає конфігурацію зворотних зв'язків (відводів) h_j в генераторі зі зсувним регістром. Інакше кажучи, якщо в многочлена h(X) коефіцієнт h_j = 1, це означає, що відвід h_j у схемі генератора наявний, якщо ж у многочлена h(X) коефіцієнт h_j = 0, то відвід h_j в схемі генератора є відсутній. У якості h(X) необхідно обирати незвідний примітивний многочлен. За такого обрання многочлена h(X) зі старшим степенем m генератор забезпечує видавання псевдовипадкової послідовності двійкових чисел з максимально можливим періодом 2^m – 1.

Розглянемо як приклад трирозрядний зсувний регістр з лінійним зворотним зв'язком (рис. 4.2), який побудовано відповідно до незвідного примітивного многочлена

,

де коефіцієнти h₃ = 1, h₂ = 1, h₁ = 0, h₀ = 1.

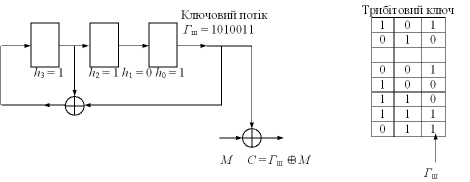
Рис. 4.2. Трирозрядний регістр зсування зі зворотними зв'язками

Нехай ключем є 101. Регістр розпочинає працювати з цього стану; послідовність станів регістру наведено на рис. 4.2. Регістр проходить через усі сім ненульових станів – і знову повертається до свого початкового стану 101. Це є найдовший період даного регістру з лінійним зворотним зв'язком. Така послідовність називається послідовністю максимальної довжини для зсувного регістра (Maximal Length Shift Register Sequence – MLSRS). За будь-якого цілого m існує m-бітова послідовність MLSRS з періодом 2^m – 1. Зокрема за m = 100 послідовність матиме період 2¹⁰⁰–1 і не повторюватиметься 10¹⁶ років при передаванні лініями зв'язку зі швидкістю 1 Мбіт/с.

У нашому прикладі початковою послідовністю (гамою шифру) Г_ш зсувного регістру зі зворотним зв'язком є послідовність 1010011, котра циклічно повторюється. У цій послідовності є чотири одиниці й три нулі і їхній розподіл є настільки близький до рівномірного, наскільки це є можливе в послідовності, котра має довжину 7. Якщо розглянути пари послідовних бітів, то пари 10 та 01 з'являються двічі, а пари 00 та 11 – одноразово, що знову стає настільки близьким до рівномірного розподілу, наскільки це є можливо. У разі послідовності максимальної довжини для m-розрядного регістру ця властивість рівнорозподілюваності поширюється на трійки, четвірки й т.д. бітів, аж до m-бітових груп. Внаслідок такої близькості до рівномірного розподілу послідовності максимальної довжини часто використовуються в якості псевдовипадкових послідовностей у криптографічних системах, котрі імітують роботу криптостійкої системи одноразового шифрування.

Хоча така криптографічна система здійснює імітацію передбачувано криптостійкої системи одноразового шифрування, сама вона не відрізняється стійкістю і може бути розкрита за кілька секунд роботи комп'ютера за умови наявності відомого вхідного тексту.

Якщо відводи регістру зі зворотним зв'язком зафіксовано, то для віднайдення початкового стану регістру надто знати m бітів вхідного тексту. Щоб віднайти m бітів ключового потоку, m бітів відомого вхідного тексту складають за модулем 2 з відповідними m бітами шифротексту. Отримані m бітів дають стан зсувного регістру зі зворотним зв'язком у зворотному напрямку на певний момент часу. Потім, моделюючи роботу регістру у зворотному напрямку, можна визначити його початковий стан.

Якщо відводи регістру зі зворотним зв'язком не є фіксовані, а є частішою ключа, то досить 2^m бітів відомого вхідного тексту, аби порівняно швидко визначити розташування відводів регістру та його початковий стан.

Нехай S(i) – вектор-стовпець, який складається з m символів 0 та 1 й визначає стан регістра в i-ий момент часу. Тоді

, (4.9)

де А – матриця розміром mm, котра визначає положення відводів регістру зі зворотним зв'язком.

Для трирозрядного регістру (див. рис. 4.2)

.

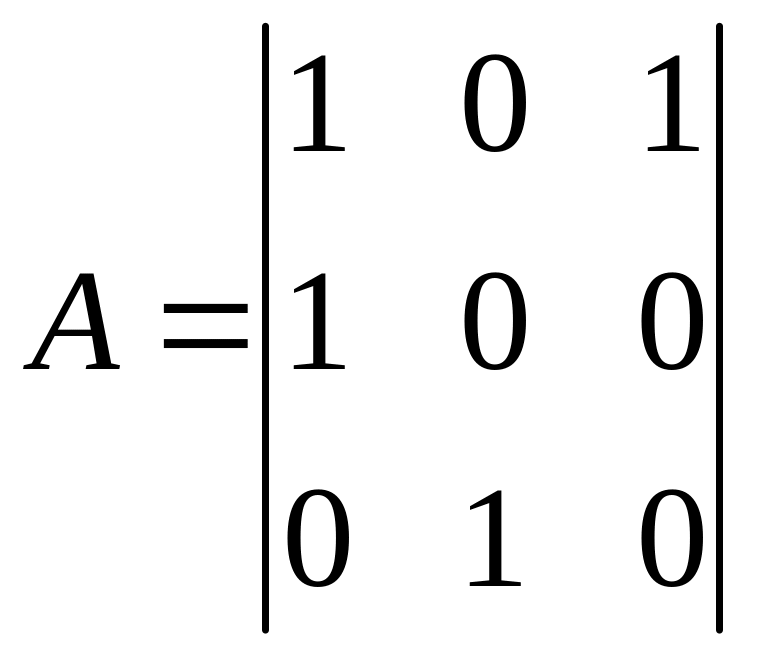Матриця A завжди має таку структуру: у її першому рядку відбито послідовність відводів у регістрі, безпосередньо під головною діагоналлю розташовуються одиниці, а в решті позицій – нулі.

2m бітів відомого вхідного тексту дають змогу обчислити 2m послідовних бітів ключового потоку. Для спрощення позначень припустімо, що це – перші 2m бітів ключового потоку. Отже,

• S(1) – перша група m відомих бітів ключового потоку;

• S(2) – наступна група (розпочинаючи з номера 2) з m відомих бітів ключового потоку;

• S(m + 1) – остання група з m відомих бітів ключового потоку.

Далі можна утворити дві матриці розміром mm:

X(1) = [S(1), S(2), ..., S(m)];

X(2) = [S(2), S(3), ..., S(m+1)];

пов'язані співвідношенням

X(2) = A·X(1) mod 2.

Можна довести, що для будь-якої послідовності максимальної довжини матриця Х(1) завжди є несингулярна, тому матрицю A можна обчислити як

A = X(2)[X(1)]^-1 mod 2.

Обертання матриці X(1) потребує (щонайбільше) біля m³ операцій, тому легко виконується за будь-якого поміркованого значення m.

Для криптографії послідовності максимальної довжини MLSRS можна зробити більш криптографічно стійкими, використовуючи нелінійну логіку. Зокрема, як ключовий потік використовується нелінійно "фільтрований" вміст зсувного регістру, а для отримання послідовності максимальної довжини – лінійний зворотний зв'язок, як це подано на рис. 4.3.

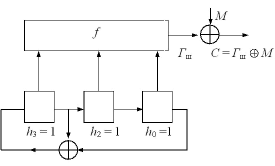
Рис. 4.3. Лінійний зсувний регістр з нелінійними логічними ланцюгами на виході

Функція f має обиратися таким способом, аби забезпечити оптимальний баланс поміж нулями й одиницями, а "фільтрована" послідовність має розподіл, близький до рівномірного. Необхідно також, аби "фільтрована" послідовність мала великий період. Якщо (2^m – 1) є простим числом (як у прикладі: за m = 3 маємо 2³–1 = 7), то "фільтрована" послідовність може мати період (2^m – 1) (при обранні структури зсувного регістру відповідно до незвідного примітивного многочлена h(X) степеня m). До згаданих значень m належать, зокрема, такі: 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, а отримані в такий спосіб прості числа називаються простими числами Мерсена.

Незважаючи на те, що "фільтровану" початкову послідовність зазвичай не можна отримати за допомогою m-розрядного зсувного регістру з лінійним зворотним зв'язком, її завжди можна отримати за допомогою зсувного регістру більшої довжини з лінійним зворотним зв'язком. Регістр довжиною (2^m – 1) завжди дасть змогу це зробити, а іноді для цього придатний і більш короткий регістр.

1 Матеріал з Вікіпедії – вільної енциклопедії. http://uk.wikipedia.org/wiki/Історія_криптографії

2 Лео́н-Батті́ста Альбе́рті (Alberti *18 лютого 1404 р., Генуя – †20 квітня 1472 р.) – італійський архітектор, вчений, письменник і музикант епохи Відродження. Уславлений теоретик мистецтва, автор проектів архітектурних споруд в різних містах Італії ранішньої доби Відродження. Сам не будував, за його проектами будували місцеві архітектори – практики. Його архітектурні ідеї, однак, мали значний вплив на розвиток архітектури Італії доби Високого Відродження. Леон-Баттіста Альберті створив новий тип католицького плану храму з урахуванням грецького хреста, а також з архітектурними елементами давньоримської архітектури. Залишив багатий теоретичний спадок. На широке розповсюдження ідей Альберті зіграли мода на античність в італійському суспільстві, авторитет самого Альберті, використання в творах вульгати (некласичного варіанту латини) і життя в Римі, що був відомим мистецьким центром тогочасної Італії.

3 Доктор Огюст Керкгоффс (Auguste Kerckhoffs, *19 січня 1835-1903 рр.) – нідерландський лінгвіст і криптограф, професор Паризької вищої школи комерції в другій половині XIX ст. У російських джерелах зустрічаються різні переклади прізвища (Керкхофф, Кирхгоф, Керкгоффс, Керхофс, Керкхоффс), що створює деяку плутанину. Керкгоффс народився в місті Нют, Нідерланди. При хрещенні отримав ім'я Жан Вільгельм Губерт Віктор Франсуа Олександр Огюст Керкгоффс фон Ніувенгоф, нідерл. Jean-Guillaume-Hubert-Victor-Fran ois-Alexandre-Auguste Kerckhoffs von Nieuwenhof. Огюст закінчив Льєжський університет, викладав в Нідерландах і у Франції. Автор книги "Військова криптографія" (опублікована в 1883 році), в якій сформулював відповіді на питання, актуальність яких для криптографії позначилася лише в XX ст. У стислій, системній формі, Огюст Керкгоффс виклав вимоги до криптографічних систем, а також показав найважливіше значення криптоаналізу для їх перевірки і підтвердження стійкості. Одна з вимог тепер відома як принцип Керкгоффса.

4 Клод Елвуд Шеннон (англ. Claude Elwood Shannon) (*30 квітня, 1916 – †24 лютого, 2001) – американський інженер – електрик і математик, "батько теорії інформації". Шеннон відомий тим, що запропонував теорію інформації в науковій статті, опублікованій в 1948 році. Йому також приписують винайдення теорії проекту цифрового комп'ютера та цифрового каналу в 1937 році, коли, будучи 21-річним студентом в Массачуссетському технологічному інституті, він написав дисертацію, в якій демонструє, що з допомогою електричного застосування Булевої алгебри можна сконструювати та розв'язати будь-які логічні та числові зв'язки.

5 Плутарх (грец. Πλούταρχος, лат. Plutarch, близько 46 120 нашої ери – давньогрецький письменник, історик і філософ-мораліст. Автор знаменитого манускрипту "Порівняльні життєписи" і низки філософських творів, написаних у руслі традиції платонізму.

6 Полі́бій (грец. oλιβιος, лат. Polybius, близько 201 р. до н. е., Мегалополь, Аркадія – близько 120 р. до н. е.) – давньогрецький історик, державний і військовий діяч, автор "Загальної історії" ("Історії") в 40 томах, що охоплюють події у Римі, Греції, Македонії, Малій Азії та в інших регіонах з 220 р. до н. е. по 146 р. до н. е. З книг "Історії" повністю збереглись тільки перші 5, інші дійшли в більш-менш детальних переказах. Всі інші праці Полібія не збереглись. Керуючись вченням стоїків про передбачення, він прийшов до метафізики історії, яка розглядала останню як боротьбу народів і окремих особистостей проти влади долі.

7 Ю́лій Це́зар (лат. Imperator Gaius Iulius Caesar – Імператор Гай Юлій Цезар (Га́йус Ю́ліус Кай́сар)) (*13 липня 100 р. до н. е. – †15 березня 44 р. до н. е.) – давньоримський державний і політичний діяч, полководець, письменник. Діяльність Цезаря докорінно змінила культурний і політичний вигляд Західної Європи і залишила визначний слід в житті наступних поколінь європейців.

8 Іоганн Трітемій (лат. Iohannes Trithemius, *1 лютого 1462 р. – †13 грудня 1516 р.) – автор книг з історії, криптографії та окультизму. Його ім'я – латинізована форма назви його рідного міста Тріттенхайм. Іоганн Хайденберг (його ім'я при народженні) закінчив університет Гейдельбергський. Коли в 1482 році він повертався додому, снігова буря змусила його сховатися в бенедиктинському абатстві Спонхайма. Він вирішив залишитися там і незабаром, вже в 1483 році, був вибраний абатом. Він зробив зусилля до збільшення бібліотеки абатства, довівши її з 50 до 2000 книг, і придбав репутацію мага. У 1506 році за пропозицією єпископа Вюрцбургського Трітемій став абатом у абатстві св. Іакова у Вюрцбурге, і займав цей пост до кінця життя. Вчителем Трітемія називають історика Рудольфа Агріколу, а серед його учнів відомі Корнелій Агріппа і Парацельс.

9 Шифр Плейфера або квадрат Плейфера – ручна симетрична техніка шифрування, в якій вперше використана заміна біграм. Винайдена в 1854 році Чарльзом Уїтстоном, але названа іменем Лорда Лайона Плейфера, який упровадив цей шифр в державні служби Великобританії. Шифр передбачає шифрування пар символів (біграм) замість одиночних символів, як в шифрі підстановки і в складніших системах шифрування Віженера. Таким чином, шифр Плейфера стійкіший до зламування порівняно з шифром простої заміни, оскільки ускладнюється частотний аналіз. Він може бути проведений, але не для 26 можливих символів (латинський алфавіт), а для 2626=676 можливих біграм. Аналіз частоти біграм можливий, але є значно важчим і вимагає набагато більшого об'єму зашифрованого тексту.

10 Шифр Лестера Хілла (Lester Hill) – поліграмний шифр підстановки, який базується на лінійній алгебрі. Лестер С. Хілл винайшов цей шифр в 1929, і це був перший шифр, який давав змогу на практиці (хоча і насилу) оперувати більш ніж з трьома символами разом. Подальше обговорення шифру передбачає початкові знання матриць.

11 Шифр Віженера (фр. Chiffre de Vigenere) – метод поліалфавітного шифрування буквеного тексту з використанням ключового слова. Цей метод є простою формою багатоалфавітної заміни. Шифр Віженера винаходився багато разів. Вперше цей метод описав Джован Баттіста Беллазо (італ. Giovan Battista Bellaso) в книзі La cifra del. Sig. Giovan Battista Bellasо в 1553 році, проте в XIX столітті отримав ім'я Блеза Віженера, французького дипломата. Метод простий для розуміння та реалізації, він є недоступним для простих методів криптоаналізу.

12 Ідеї Віженера знайшли розвиток у ряді інших подібних періодичних систем. Наприклад в "шифрі Гронсфельда", придуманому в 1734 році бельгійцем Хосе де Бронкхором, графом де Гронсфельдом, військовим і дипломатом, начальником першого дешифровального відділу в Німеччині. Замість буквеного гасла-ключа він узяв числовий, такий, що складається з декількох цифр, що легко запам'ятовуються. Замість великої громіздкої квадратної таблиці використовувався тільки один алфавіт з правильним розташуванням літер. Буква шифрованого тексту замінювалася буквою алфавіту, віддаленою від неї управо або вліво на кількість знаків, що дорівнює відповідній цифрі ключа. Легко переконатися, що шифр Гронсфельда є окремим випадком більш загальної системи шифрування Віженера.

13 Сер Чарльз Уїтстон (англ. Sir Charles Wheatstone; 1802-1875 рр.) – англійський фізик, автор багатьох винаходів. У 1837 р. в співпраці з Уїлямом Куком отримав патент на електромагнітний телеграф і створив першу ls.xe телеграфну лінію в Англії. Це був так званий стрілочний телеграф: стрілка на приймачі показувала букви алфавіту, розташовані колом на зразок цифр в годиннику. Запропонував мостовий метод електричних вимірювань. Так званий міст Вітстона (Уїтстона) слугує основою сучасних гальванометрів, який балансує вимірювані струми так, що стає можливим вимірювання коливань цих струмів. Є винахідником стереоскопа – апарату для перегляду тривимірних зображень. У 1829 р. запатентував музичний інструмент Концертина.

14 Код Бодо (названий на честь Жана Моріса Еміля Бодо, 1845-1903 рр.) – цифровий, спочатку синхронний, 5-бітовий код. Пізніше він став міжнародним стандартом CCITT-1. На його основі був розроблений код CCITT-2, що став стандартом у телеграфії. Початковий код (пізніше Міжнародний телеграфний алфавіт № 1 (ITA1), CCITT-1) розробив Еміль Бодо 1870 р. для свого телеграфу. Код вводився прямо клавіатурою, що складається з п'яти клавіш, натискання або не натисканням клавіші відповідало передачі або непередачі одного біта в пятибітному коді. Максимальна швидкість передачі – трохи більше 190 знаків на хвилину (16 біт в секунду, 4 Бода).