§ 10. Двудольный граф

Двудольный граф F (или граф паросочетаний)  это граф, для которого можно выполнить разбиение его множества вершин V на два подмножества V₁ и V₂ таким образом, что каждое ребро графа F соединяет вершины из разных множеств.

Если в двудольном графе F каждая вершина из V₁ соединена ребром со всеми вершинами из V₂, то F называется полным двудольным графом. Обозначение: K_{|V1|, |V2|}. Понятно, что в графе K_{|V1|, |V2|} имеется |V₁|  |V₂| ребер.

Теорема Кёнига. Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

  Пусть граф F  двудольный. Тогда каждый простой цикл v₁, v₂, ... v_n, v₁ графа F содержит вершины из V₁, скажем, с нечетными номерами, и вершины из V₂  с четными, так что длина этого цикла является четным числом.

 Предположим, не теряя общности, что F  связный граф (поскольку каждую компоненту графа F можно рассматривать отдельно). Выберем произвольную вершину v₁ V и обозначим через V₁ множество, состоящее из v₁ и всех вершин, находящихся в графе F на четном расстоянии от v₁; определим V₂, = V \ V₁.

Так как все простые циклы графа F имеют четную длину, то каждое его ребро соединяет вершину из множества V₁ с вершиной из множества V₂. В самом деле, предположим, что существует ребро (u, v), соединяющее две вершины из множества V₂. Тогда две кратчайшие простые цепи  из вершины v₁ к вершине v и из вершины v₁ к вершине u  в объединении с ребром (u, v) образуют цикл нечетной длины. 

Из теоремы Кёнига следует, что в каждом из двудольных графов нет циклов, содержащих три вершины и три ребра (треугольников).

§ 11. Планарность

Граф укладывается на поверхности S, если его диаграмму можно так нарисовать на S, что никакие два его ребра не пересекаются

Граф называется планарным, если его можно уложить на плоскости; плоский граф  это граф, уже уложенный на плоскости.

Пример. Граф 3.23, а является планарным, так как он изоморфен плоскому графу 3.23, б. Граф 3.23, в планарным не является.

Рис. 3.23.

Области, на которые плоский граф разбивает плоскость, называются гранями. Количество граней будем обозначать r.

Пример. Граф 3.23, б разбивает плоскость на четыре грани: r = 4; при этом грани I, II, III  внутренние, а неограниченная грань IV  внешняя.

Изучение плоских графов начнем с минимального связного графа, состоящего из единственной вершины и не имеющего ребер. Любые точки плоскости, не совпадающие с вершиной этого графа, можно соединить ломаной линией, не проходящей через нее. Значит у минимального графа на плоскости одна связная область.

Любой другой связный плоский граф F*(V*, E*) может быть порожден из связного плоского графа F(V, E) с меньшим количеством вершин или ребер с помощью одной из следующих операций.

Рис. 3.24.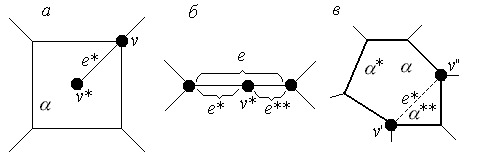

1. Добавление вершины степени 1. Внутри некоторой грани  ставится новая вершина v* и соединяется новым ребром e* с некоторой вершиной v, расположенной на границе грани  (рис. 3.24, а).

2. Добавление вершины степени 2. Внутри некоторого ребра e ставится новая вершина v*. Таким образом, это ребро разбивается на два  e* и e** (рис. 3.24, б).

Очевидно, что для операций 1 и 2: |V*| = |V| + 1; |E*| = |E| + 1; r* = r.

3. Разбиение области. Новое ребро e* соединяет v’ вершины и v’’, расположенные на границе грани , и лежит в этой грани (рис. 3.24, в). Из теоремы Жордана следует, что грань разбивается на две  * и **. Значит, для операции 3: |V*| = |V| ; |E*| = |E| + 1; r* = r + 1.

Докажем, что при помощи указанных операций можно породить любой связный плоский граф.

 Будем использовать обратные операции: удаление вершин степени 1 и 2, а также разрыв цикла. Рассмотрим не минимальный связный плоский граф F*(V*, E*). Если в нем есть вершина степени 1 или 2, то можно произвести операцию удаления этой вершины, причем в результате получится связный плоский граф F(V, E). Наоборот, граф F*(V*, E*) может быть получен из графа F(V, E) операцией добавления вершины степени 1 или 2.

Пусть теперь степени всех вершин графа F*(V*, E*) не меньше, чем 3. Значит, сумма  степеней всех вершин не меньше утроенного числа вершин:   3|V*|. С другой стороны, по лемме о рукопожатиях сумма  равна удвоенному числу ребер:  = 2|E*|. Отсюда |E*|  3|V*|/2.

Цикломатическое число графа F*(V*, E*) равно |E*|  |V*| + 1  |V*|/2 + 1 > 0, значит, в нем есть некоторый цикл Z. Если удалить из графа F* какое-нибудь ребро цикла Z, то F* останется связным. Наоборот, граф F*(V*, E*) может быть получен из связного плоского графа F(V, E) операцией соединения вершин v’ и v’’ ребром e*. Так как при этом возникает новый цикл Z, то область , по которой проходит ребро e*, разбивается на две. 

Теорема Эйлера. Пусть F(V, E)  связный плоский граф. Тогда количества его вершин, ребер и граней связаны соотношением:

|V|  |E| + r =2. (13.1)

 1. В минимальном связном плоском графе: |V| =1; |E| = 0; r =1, значит, |V|  |E| + r =2.

2. Пусть соотношение выполняется для всех связных плоских графов F(V, E) при |E| = k.

3. Докажем, что оно выполняется для всех связных плоских графов F*(V*, E*) при

|E*| = k+1.

Как было показано выше, граф F* можно получить из графа F при помощи операций 1, 2, 3. Если была использована операция 1 (или 2), то

|V*|  |E*| + r* = (|V|+1)  (|E|+1) + r = |V|  |E| + r = 2.

Если была использована операция 3, то

|V*|  |E*| + r* = |V|  (|E|+1) + (r+1) = |V|  |E| + r = 2. 

Следствие 1. Если F(V, E)  связный планарный граф (|V|>3), то |E|  3|V|  6.

 Каждая грань ограничена, по крайней мере, тремя ребрами, каждое ребро является границей не более чем двух граней, т.е. 2|E|  3r или r  2|E|/3. Тогда, из соотношения Эйлера,

2 = (|V|  |E| + r)  (|V|  |E| + 2|E|/3), отсюда |E|  3|V|  6. (13.2)



Следствие 2. Графы K₅ и K_3,3 (рис. 3.25) не являются планарными.

 Если бы граф K₅ был планарным, то для него выполнялось бы соотношение (13.2):

(10 = |E|)  (3|V|  6 = 9), т.е. 10  9. Последнее неравенство является ложным.

В графе K_3,3 нет треугольников, значит, в его плоской укладке (если такая существует) каждая грань ограничена не менее чем четырьмя ребрами и, следовательно, 2|E|  4r или r  |E|/2. По формуле Эйлера

2 = (|V|  |E| + r)  (|V|  |E| + |E|/2), отсюда |E|  2|V|  4.

Для K_3,3 имеем: (|E| = 9)  (2|V|  4) = 8. ), т.е. 9  8. Последнее неравенство является ложным.



Рис. 3.25.

Следствие 3. В любом планарном графе F(V, E) найдется вершина, степень которой не больше 5.

 Предположим, что таких вершин нет, т.е. степень каждой вершины не менее 6. По лемме о рукопожатиях имеем:

2|E| =  6|V|, т.е. |E|  3|V|, что противоречит соотношению (13.2) 

Критерий, характеризующий планарные графы, был предложен в 30-х гг. нашего столетия русским математиком Понтрягиным и польским математиком Куратовским.

Теорема 3.1 (Понтрягина  Куратовского). Граф является плоским тогда и только тогда, когда он не имеет подграфом графа K₅ или графа K_3,3.

Доказательство этой теоремы здесь не приводится ввиду его сложности. Интересующиеся могут найти его, например, в [1].