17

Элементы теории графов

§ 1. Графы, их вершины, рёбра и дуги

Рассмотрим множество V={v₁,v₂,...,v_n}, n2, и множество E={e₁,e₂,...,e_m}, элементами e_k которого являются двухэлементные подмножества {v_i, v_j} множества V. Пара множеств V и E называется неориентированным графом F(V,E) с множеством вершин V и множеством ребер E. При этом говорят, что неориентированное ребро e_k соединяет вершины v_i, v_j или ребро e_k и вершины v_i, v_j инцидентны. Вершины v_i и v_j называют смежными.

Граф F(V,E) может быть изображен геометрически. Для этого некоторые n точек трехмерного пространства помечаются элементами множества вершин V и вершины v_i и v_j соединяются линией, если {v_i, v_j} Е. Геометрическое изображение графа будем называть диаграммой.

Пример 3.1. Пусть V={v₁,v₂,v₃,v₄}, а элементами множества E являются все возможные множества вида {v_i, v_j} при i,j=1,2,3,4; ij. Диаграмма графа приведена на рис. 3.1, а.

Пусть теперь множество E={e₁,e₂,...,e_m} представляет собой некоторое бинарное отношение на множестве V (EVV). Тогда пара множеств V и E называется ориентированным графом (орграфом) F(V,E) с множеством вершин V и множеством ребер E.

Ребро ориентированного графа называется дугой. Для дуги e_k=(v_i, v_j) вершина v_i называется начальной, а v_j  конечной. Иными словами, ребро e_k выходит из вершины v_i и заходит в вершину v_j. Как и в случае неориентированного ребра, дуга e_k инцидентна вершинам v_i и v_j, а вершины v_i и v_j инцидентны дуге e_k. Вершины v_i и v_j также называют смежными.

Ребро, у которого концевые точки совпадают, называется петлей.

Пример 3.2. Пусть V={3, 8, 24}. Зададим на этом множестве отношение

E={(u,w)/ u - делитель w; u,wV}={(3,3), (3,24), (8,8), (8,24), (24,24)}.

Рис. 3.1.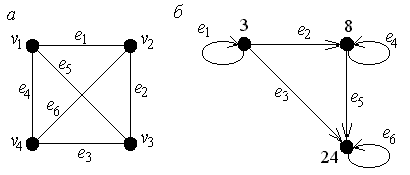

Диаграмма графа приведена на рис. 3.1, б.

Из приведенных определений графов следует, что в них отсутствуют кратные, или параллельные, ребра, соединяющие одни и те же пары вершин. Кроме того, в неориентированном графе не допускаются петли. Однако иногда удобно снять указанные ограничения.

Граф, содержащий кратные ребра называется мультиграфом. Граф, содержащий петли и (или) кратные ребра, называется псевдографом.

Два графа F и F* изоморфны, если существует такое взаимно однозначное соответствие между множествами их вершин V и V*, что вершины соединены рёбрами в одном из графов тогда и только тогда, когда соответствующие им вершины соединены в другом графе. Если рёбра ориентированы, то их направления также должны соответствовать друг другу. Все изоморфные графы имеют одинаковые свойства.

Вершина, не инцидентная никакому ребру, называется изолированной. Граф, состоящий только из изолированных вершин, называется нуль-графом (пустым графом) и обозначается через 0. Для нуль-графа множество ребер  пустое: Е=.

Другим важным частным случаем является полный граф, в котором каждая вершина множества V соединена ребром со всеми остальными вершинами этого множества. В дельнейшем полный неориентированный граф с n вершинами будем обозначать K_n. В ориентированном полном графе для каждой пары вершин имеются два ребра: по одному в каждом направлении.

Пример. На рис. 3.1, а представлен граф K₄.

Граф H(V_H, E_H) называется частью графа F(V, E) (обозначение: HF), если V_H  V, E_H  E. Нуль-граф является частью каждого графа.

Рис. 3.3.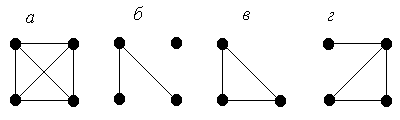

Особенно важный тип частей составляют подграфы. Пусть V*  V. Подграф F*(V*, E*) графа F  это такая часть графа F(V, E), множество рёбер E* которого составляют все рёбра графа F(V, E), оба конца которых лежат в V*.

Если V* = V, то подграф F*(V*, E*) совпадает с F(V, E). В противном случае подграф F*(V*, E*) называется собственным подграфом графа F*(V*, E*). Для единичной вершины V* = {а} подграф F*(V*, E*) состоит из петель в а.

Пример (рис. 3.3). Для графа 3.3, а граф 3.3, б является частью, но не является подграфом, тогда как граф 3.3, в является для графа 3.3, а как частью, так и подграфом.

Число неориентированных графов с n вершинами

Пусть имеется n вершин, помеченных соответственно: v₁, v₂,..., v_n. Подсчитаем количество различных диаграмм, которые можно построить на этих вершинах. Максимальное количество ребер в графе определяется количеством способов, которыми из n вершин можно выбрать две: =С_n². Для каждого ребра существует две возможности: либо его проводят, либо нет. В соответствии с правилом произведения в комбинаторике, количество диаграмм, а значит, и графов, равно 2^.

Число неориентированных графов с n вершинами и m ребрами

Пусть по-прежнему имеется n вершин, помеченных соответственно: v₁, v₂,..., v_n. Графов с m ребрами столько, сколько существует способов из всех =С_n² ребер выбрать m ребер, т.е С_^m.