6.4 Метод Ньютона

Пусть для урав­нения

(1)

на интервале отделен корень .

Пусть имеется некоторое приближение корня точка – . Тогда, (к + 1)-ое приближение корня будем искать в виде:

, (2)

где – шаг, который подлежит определению.

Чтобы определить , подставим разложим функцию в ряд Тейлора в окрестности точки

.

Заменим в этом разложении на корень

.

Но – корень, так что

.

Отбросим в этом разложение малое слагаемое . Поскольку точка близка к корню , то разность по модулю мала, следовательно величина будет тем более малой

.

Однако корнем линейного уравнения буде уже не точка , а близкая к ней точка которую обозначим

.

Заменяя в этом уравнении разность , получаем

.

Подставляем в (2), получаем

(3)

Выражения (3) называют итерационным мето­дом Ньютона уточнения корней нелинейного уравнения (1). Метод Ньютона называют также методом касательных. В этом методе на каждой итерации к графику функ­ции проводится касательная в точке до пересе­чения с осью абсцисс (рис.). Уравнение касательной имеет вид

.

Полагая в этом уравнении и , получим формулу Ньютона (3).

Справедлива следующая теорема.

Теорема (достаточные условия сходимости метода Ньютона). Пусть определена и дважды дифференцируе­ма на отрезке , причем , производные и знакопостоянны и . Тогда исходя из начального приближения , удовлетворяющего неравен­ству , можно построить последовательность (3), сходящуюся к единственному корню уравнения (1) на отрезке с погрешностью, оцениваемой неравенством

(4)

где , , .

Согласно теореме за начальное приближение можно принять один из концов отрезка , а именно

(5)

Поскольку верхняя оценка (4) сложна для вычисления, на практике итерационный процесс останавливают при выполнении условия , , где — заданная точность.

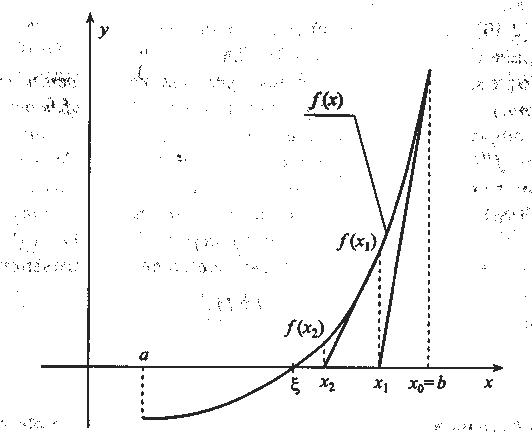
Рис. 7. Метод Ньютона

Для случая, приведенного на рисунке, за начальное прибли­жение принимается , так как .

45