6. Численное решение нелинейных уравнений и систем

6.1 Отделение корней

Одна из простейших задач, часто возникающая при математическом моделировании различных систем, – нахождение приближенных значений корней нелинейных уравнений и трансцендентных уравнений, например .

Всякое нелинейное алгебраическое или трансцендентное урав­нение с одним неизвестным может быть записано в виде

(1)

где - функция вещественного переменного.

Решением (или корнем) уравнения (1) называется такое зна­чение , при котором функция обращается в нуль, т. е. .

Корень уравнения (1) называется простым, если . В противном случае (т.е. ) корень называ­ется кратным. Целое число т назовем кратностью корня , ес­ли для значений и .

Вещественный корень уравнения (1) геометрически пред­ставляет абсциссу точки пересечения или касания графика функции и оси Ох.

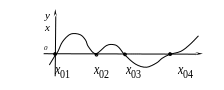
Функция (график которой изображен на рисунке) имеет четыре корня. Корни и - простые, и - кратные. Ес­ли какой-либо вещественный корень является двукратным, напри­мер, то кривая касается оси Ох в точке, где .

Рис. 1. Простые и кратные корни уравнения (1)

Задача отыскания простых корней является существенно более простой (и чаще встречающейся), чем задача отыскания кратных корней. В действительности большинство методов решения урав­нения (1) ориентировано именно на вычисление простых кор­ней.

Процесс нахождения приближенных значений корней нелиней­ного уравнения осуществляется в два этапа. Первый этап называет­ся этапом локализации (или отделения) корней, второй - эта­пом уточнения корней до заданной степени точности.

Корень уравнения (1) считается отделенным (или лока­лизованным) на отрезке , если на этом отрезке уравнение (1) не имеет других корней.

Отрезок , содержащий только один корень уравнения (1), называют отрезком локализации корня (его длину стараются по возможности сделать минимальной).

Отделить корни - это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень. Отделение корней можно произвести графическим методом, если построить график функции . Точки пересечения графика с осью Ох дают значения корня, и по графику легко определить два числа а и b, между которыми заключен только один корень.

Пример. Определить графически, между какими целыми числами заключены корни уравнения . Построим график функции и определим абсцис­сы точек пересечения этого графика с осью Ох (рис. 1.). Кривая пересекает ось Ох в двух точках; следовательно, уравнение имеет два вещественных корня. Из чертежа видно, что корни принадлежат отрезкам , .

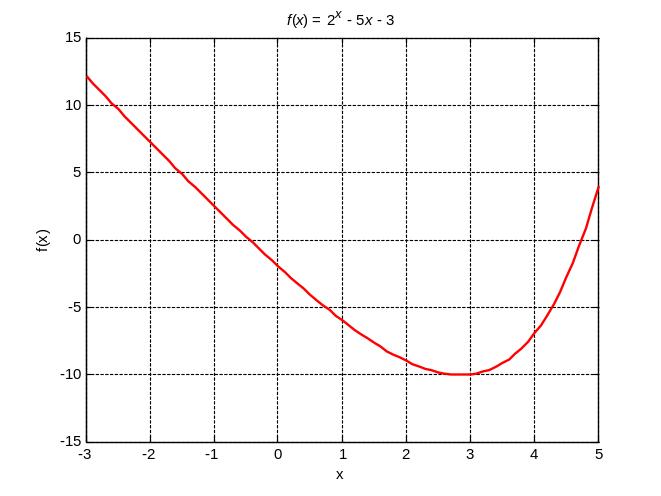
Рис. 2. Графический метод отделения корней

Графический метод отделения корней не обладает большой точ­ностью. Он дает возможность грубо определить интервалы изоля­ции корня. Далее корни уточняют одним из способов, указанных ниже.

Предположим, что — приближенное значение корня, — его точное значение. Возникает вопрос, какова погрешность приближенного значения корня по сравнению с его точ­ным значением , если последний неизвестен?

Для этого построим невязку , т. к. . Применим к невязке теорему Лагранжа о конечных прира­щениях:

,

откуда

.

Так как точное значение неизвестно, эту погрешность за­меняют верхней оценкой:

. (*)

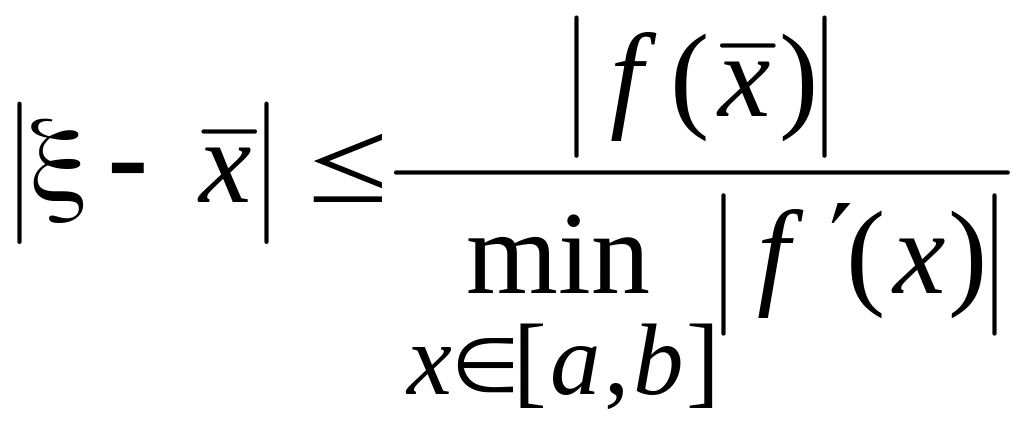Оценка погрешности (*) является довольно грубой. Поэто­му в каждом итерационном методе уточнения корней, в силу ограничений применения метода, можно вывести свою оценку погрешности.