6.8 Спектральное разложение стационарной случайной функции

К случайным процессам классический гармонический анализ неприменим, так как случайная функция определяется не одной реализацией, а их семейством. Основная идея, дающая возможность применять ряды Фурье и интеграл Фурье к случайным процессам, состоит в усреднении спектральных разложений аналогично уже известному усреднению по времени. При этом спектральные разложения случайных процессов осуществляются не по отношению к «кривым мгновенных значений», а по отношению к кривым, представляющим собой квадраты мгновенных значений. Поэтому в этих разложениях отсутствует информация о фазах гармонических составляющих случайного процесса.

Спектральным разложением случайной функции называют представление ее в виде суммы бесконечного множества гармонических колебаний со случайными амплитудами и случайными фазами.

Если процессы периодические, то применяют ряды Фурье, если же апериодические – интеграл Фурье.

Спектральное разложение стационарной случайной функции на конечном промежутке времени. Пусть дана случайная функция X(t) в промежутке [0,T] с математическим ожиданием и корреляционной функцией , где . Требуется произвести спектр – разложение функции X(t).

Задача будет решена в том случае, если стационарная случайная функция X(t) может быть представлена в виде ряда Фурье

, (6.17)

где - математическое ожидание стационарной случайной функции (гармоника нулевой частоты);

- некоррелированные случайные величины (случайные амплитуды гармоник с частотой ) с равными нулю математическими ожиданиями и попарно равными дисперсиями.

В выражении (6.17) неизвестными величинами являются дисперсии амплитуд гармоник и их частоты.

Для отыскания дисперсий амплитуд гармоник поступают следующим образом. Поскольку дисперсия суммы некоррелированных случайных функций определяется как сумма их дисперсий, то дисперсия стационарной случайной функции (6.17), равная

, (6.18)

также является суммой дисперсий гармоник со случайной амплитудой. Кроме того, дисперсия функции X(t) равна значению корреляционной функции в начале координат .

Поэтому для получения дисперсий амплитуд каждой из гармоник можно воспользоваться разложением корреляционной функции в ряд Фурье.

При изменении в промежутке [0,T] разность будет изменяться в промежутке [-T,T], где и следует рассматривать корреляционную функцию .

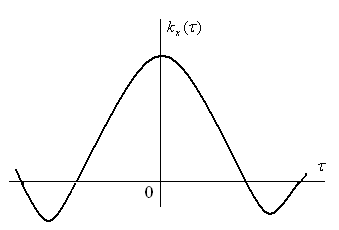
Рисунок 6.11 – Корреляционная функция

Так как корреляционная функция четна: , то ее график симметричен относительно оси ординат (рис. 6.11), то она может быть разложена в промежутке [-T,T] в ряд Фурье по косинусам:

,

где ; ; k=0,1,2,….

Коэффициенты ряда Фурье определяются по формулам

.

Учитывая, что - неслучайные величины, а потому и , и также будут неслучайными функциями, то дисперсия функции X(t) будет равна

, (6.19)

где - дисперсия амплитуды k-той гармоники.

Следовательно, дисперсия стационарной случайной функции равна сумме дисперсий амплитуд гармоник ее спектрального разложения.

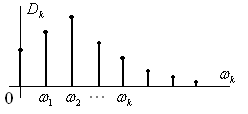
Рисунок 6.12 – Спектр дисперсии стационарной случайной функции

Распределение дисперсий по частотам можно представить в виде спектра дисперсии (энергетического спектра) случайной функции (рис.6.12). Спектральное разложение стационарной случайной функции на конечном промежутке времени представляет собой спектр дисперсии в виде отдельных дискретных значений, разделенных равными промежутками (линейчатый спектр).

Для спектрального разложения стационарной случайной функции на бесконечном промежутке времени будем рассматривать не дисперсию случайной амплитуды каждой гармоники, а среднюю плотность дисперсии, т.е. дисперсию, приходящуюся на единицу длины данного интервала частот . Обозначив расстояние между соседними частотами как , на каждом таком интервале частот построим прямоугольник площадью (рис. 6.13).

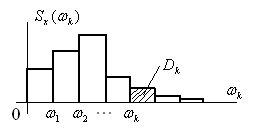
Рисунок 6.13 – Диаграмма дисперсии

Площадь полученной ступенчатой фигуры (диаграммы) будет равна дисперсии стационарной случайной функции. Так как площадь k-го прямоугольника, прилежащего к точке , равна , то высота его будет

и представляет собой среднюю плотность дисперсии на этом участке оси частот.

Неограниченно увеличивая интервал времени T, расстояние между соседними частотами будет неограниченно приближаться к нулю, а ступенчатая кривая – к некоторой плавной кривой , изображающей плотность распределения дисперсий по частотам непрерывного спектра (рис.6.14).

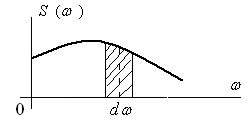
Рисунок 6.14 – График спектральной плотности стационарной случайной функции

Спектральной плотностью стационарной случайной функции называют предел отношения дисперсии, приходящейся на данный интервал частот, к длине интервала, когда она стремится к нулю, т.е.

.

Из определения спектральной плотности стационарной случайной функции следует, что площадь, ограниченная кривой и осью абсцисс, численно равна дисперсии этой функции, поэтому

. (6.20)

Спектральная плотность представляет собой зависимость дисперсии случайного процесса от частоты, поэтому ее можно трактовать как количество мощности случайного процесса, приходящуюся на единицу частоты.

Зная корреляционную функцию стационарной случайной функции X(t), с помощью прямого преобразования Фурье можно найти ее спектральную плотность:

;

, и наоборот, зная , с помощью обратного преобразования Фурье можно определить корреляционную функцию :

;

.

В последних формулах условное распространение области частот на отрицательные значения позволяет придать этой связи симметрию.

Понятие белого шума. Случайный процесс X(t) считают узкополосным, если ширина полосы спектра , занимаемого им, намного меньше частоты , т.е., если . В противном случае процесс X(t) относят к широкополосному случайному процессу.

В теории случайных процессов большое значение имеют стационарные процессы, спектральная плотность которых постоянна в широком диапазоне частот, т.е. близка к так называемому «белому шуму».

Белым шумом называют стационарный случайный процесс с нулевым математическим ожиданием и постоянной спектральной плотностью для всех частот от нуля до бесконечности, т.е.

и .

Число называют интенсивностью белого шума.

Дисперсия белого шума будет равна

.

Для этого белый шум имеет бесконечную энергию, что является причиной его физической неосуществимости. Однако белый шум является удобной математической моделью в теоретических исследованиях, поскольку любая физическая система, имея ограниченную полосу пропускания, не реагирует на гармонические колебания, лежащие вне полосы пропускания. Следовательно, всякая стационарная случайная функция может считаться белым шумом, если ее спектральная плотность остается приблизительно постоянной в пределах полосы пропускания системы.

Кроме того, корреляционная функция белого шума равна

.

На основании свойства - функции окончательно запишем, что , если и , если .

Таким образом, для белого шума отсутствует корреляция в два различных момента времени, т.е. отсутствует связь между любыми двумя различными сечениями случайного процесса.