Тема: Исследование влияния основных социально-экономических показателей на результативный признак Содержание

1. Классическая линейная модель множественной регрессии

1.1 МНК-оценка коэффициентов классической линейной модели множественной регрессии

1.2 Статистические свойства МНК-оценок в классической линейной модели множественной регрессии

1.3 Проверка гипотезы о неадекватности линейной модели выборочных данных

1.4 Проверка гипотез о незначимости коэффициентов в классической линейной модели множественной регрессии

2. Мультиколлинеарность

2.1 Внешние и формальные признаки мультиколлинеарности

2.2 Способы устранения мультиколлинеарности

3. Обобщенная линейная модель множественной регрессии с гетероскедастичными остатками

3.1 Внешние признаки и тесты для проверки гипотезы о наличии гетероскедастичности

3.1.1 Тест ранговой корреляции Спирмена

3.1.2 Тест Голдфелда-Квандта

3.2 Способы устранения гетероскедастичности

4. Обобщенная линейная модель множественной регрессии с автокоррелированными остатками

4.1 Внешние признаки и критерии для проверки гипотезы о наличии автокорреляции

4.1.1 Критерий Дарбина-Уотсона

4.2 Способы устранения автокорреляции

1 Классическая линейная модель множественной регрессии

1.1 МНК-оценка коэффициентов классической линейной модели множественной регрессии

Функция , описывающая зависимость условного среднего значения результативного признака от заданных значений аргументов, называется функцией (уравнением) регрессии.

Линейная функция регрессии имеет вид:

Тогда, линейная модель множественной регрессии будет иметь вид:

,

где - значение факторных переменных

- неизвестные коэффициенты модели множественной регрессии

- случайные ошибки модели множественной регрессии.

При построении нормальной модели множественной регрессии учитываются пять условий Гаусса-Маркова:

1) факторные переменные - детерминированные переменные, т.е. не случайные

2)

3)математическое ожидание регрессионных остатков равно нулю:

4)дисперсия регрессионных остатков равна постоянной (условие гомоскедастичности регрессионных остатков):

5) ковариация между регрессионными остатками равна нулю:

Условие некоррелированности регрессионных остатков: условия 4 и 5 можно записать одним условием 4’:

.

Общий вид нормальной модели парной регрессии в матричной форме имеет вид:

,

где

- случайный вектор-столбец значений результативной переменной;

- матрица значений факторной переменной. Первый столбец является единичным, потому что в модели регрессии коэффициент умножается на единицу;

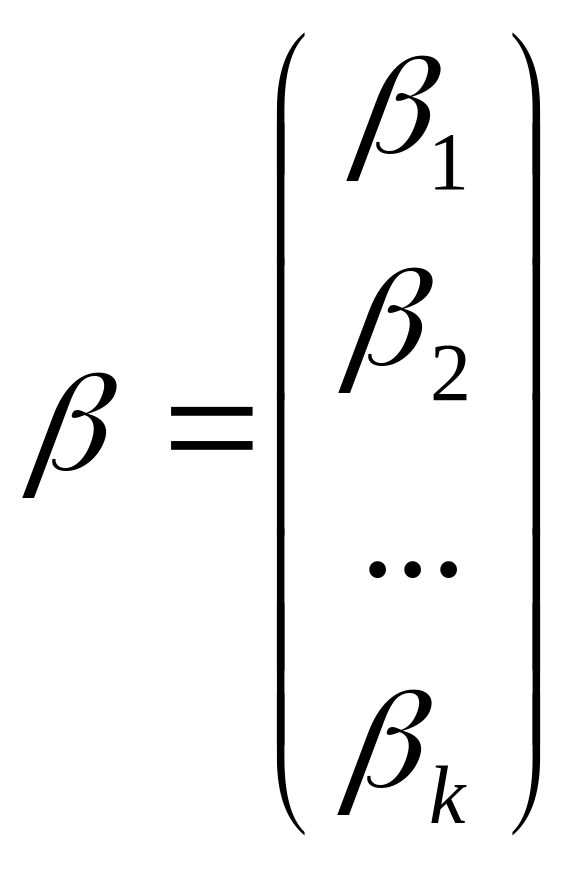
- вектор-столбец неизвестных коэффициентов модели множественной регрессии;

- случайный вектор-столбец модели множественной регрессии.

Оценку коэффициента уравнения регрессии находят из критерия минимума суммы квадратов отклонений, наблюдаемых значений от значений функции регрессии (метод наименьших квадратов):

.

Для проведения регрессионного анализа в данном примере находим показатели регрессии.

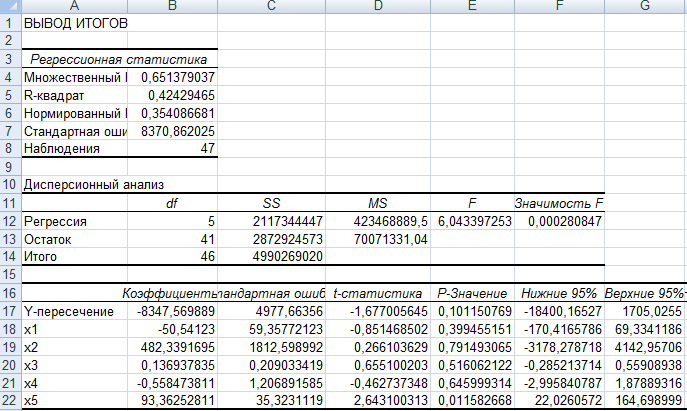
Рисунок 1 – Вид рабочего листа с выводом показателей опции Регрессия

Оценка модели регрессии выглядит следующим образом:

ŷ= –8347,569–50,541Х1+482,339Х2+0,137Х3–0,558Х4+93,363Х5

(4977,664) (59,358) (1812,599) (0,209) (1,206) (35,323)

В качестве характеристики в степени рассеивания случайной величины относительно функции регрессии используется в случае нелинейной связи корреляционное отношение, которое характеризует качество подгонки регрессии под выборочные данные.

В случае линейной регрессии корреляционное отношение называется коэффициентом детерминации. Коэффициент детерминации получается из тех соображений, что общая вариация результативного признака складывается из вариации функции регрессии, обусловленной варьированием значений объясняющих переменных (факторной дисперсии) и из вариации случайной величины относительно функции регрессии (остаточной дисперсии).

Общая дисперсия – это сумма квадратов отклонения наблюдаемых значений от его среднего значения:

Остаточная дисперсия – сумма квадратов отклонения наблюдаемых значений от модельных:

Факторная дисперсия – сумма квадратов отклонения модельных значений от среднего значения результативного признака:

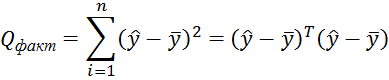
Оценка коэффициентов детерминации будет определяться по формуле:

Выборочный коэффициент детерминации характеризует долю общей вариации результативного признака у, объясняющей вариацию выборочной функции регрессии.