1.2 Статистические свойства мнк-оценок в классической линейной модели множественной регрессии.

1. Несмещенность. МНК-оценка 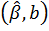является несмещенной оценкой вектора β.

2. Эффективность. Найдем ковариационную матрицу вектора оценок. Несмещенная оценка ковариационной матрицы определяется по формуле:

- несмещенная оценка остаточной дисперсии .

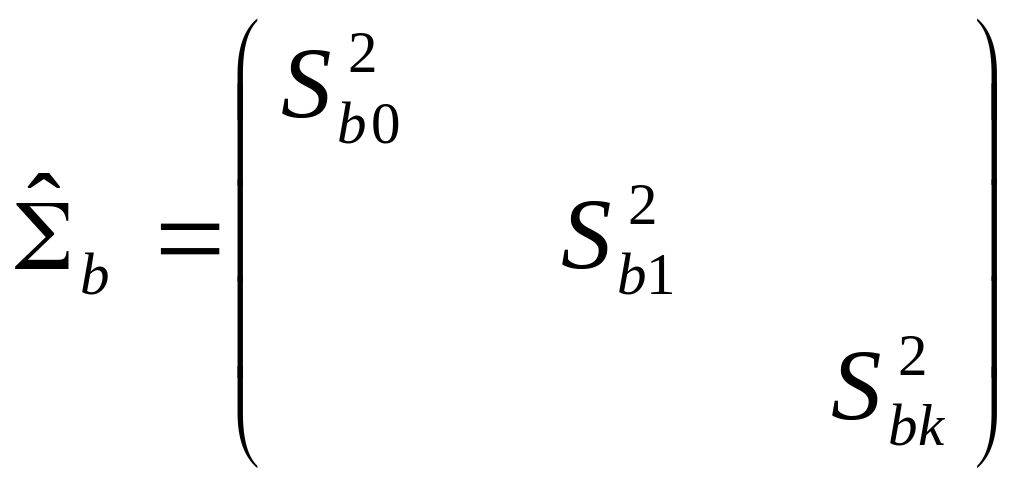
Т.к. на главной диагонали матрицы вектора оценок находятся дисперсии элементов вектора оценок b, вне главной диагонали ковариационной матрицы расположенной значения коэффициентов ковариации.

3. Состоятельность. Оценки b и 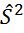являются состоятельными, тогда и только тогда, когда наименьшее собственное число матрицы 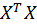стремиться к бесконечности при 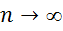. Дальнейшее изучение свойств классической линейной модели множественной регрессии проявляется при дополнительном предположении о нормальном характере распределения регрессионных остатков.

1.3 Проверка гипотезы о неадекватности линейной модели выборочных данных.

Для проверки значимости модели и значимости коэффициентов нужно убедиться, что остатки имеют нормальный закон распределения.

Построим гистограмму регрессионных остатков.

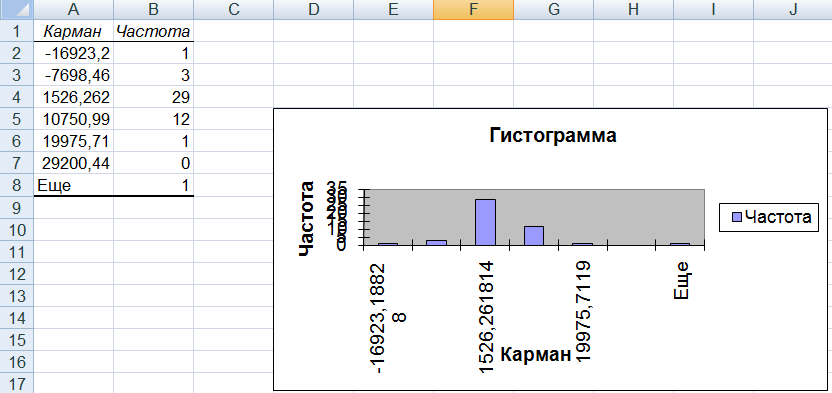
Рисунок 2 – Вывод результатов Гистограммы

Для проверки значимости построенного уравнения регрессии выдвигается гипотеза Н0: линейная модель множественной регрессии неадекватна к выборочным данным:

= ;

Альтернативная гипотеза Н1: линейная модель множественной регрессии адекватна выборочным данным:

Для проверки нулевой гипотезы строится статистика F:

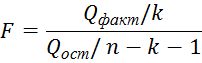
Согласно рисунку 1, наблюдаемое значение статистики F составило .

В случае справедливости нулевой гипотезы статистика имеет распределение Фишера-Снедекора, с числом степеней свободы , .

Далее проверим гипотезу традиционным образом, либо задавшись уровнем значимости и по числу степеней свободы находим критическое значение статистики F и сравниваем Fкрит (найденное по таблице Фишера-Снедекора) с Fнабл (вычисленное).

Если Н0 принимается.

Найдем критическое значение.

Вероятность – это вероятность, связанная с F-распределением ( =0,05)

Степень свободы 1 = 5

Степень свободы 2: n-k-1=47-5-1=41.

Таким образом, получаем .

Либо для программных средств сравнивая значимость нулевой гипотезы с заданным уровнем, если вероятность нулевой гипотезы больше заданного уровня значимости, то гипотеза Н0 принимается.

Так как, < , с вероятностью ошибиться 0,05 нулевая гипотеза отвергается, модель признается адекватной выборочным данным.

1.4 Проверка гипотез о незначимости коэффициентов в классической линейной модели множественной регрессии (клммр).

В случае если нулевая гипотеза о незначимости уравнения регрессии отвергнута, проверяем гипотезы о значимости коэффициентов уравнения регрессии. Выдвигается гипотеза:

(коэффициент βj незначимо отличен от нуля).

Альтернативная гипотеза (коэффициент βj значимо отличен от нуля).

Для проверки гипотез строится статистика:

,

которая в случае справедливости нулевой гипотезы имеет распределение Стьюдента с n-k-1 степенями свободы.

В данном случае: вероятность – вероятность, соответствующая двустороннему распределению Стьюдента ( ), степени свободы ( n-k-1=41).

Ткрит находим по таблице Стьюдента, если , то Н0 принимается.

Таким образом, .

Сравним наблюдаемое и критическое значения:

< , коэффициент незначим.

< , коэффициент незначим.

< , коэффициент незначим.

< , коэффициент незначим.

> , коэффициент значим.

Таким образом, < , то принимаем гипотезу , т.е. коэффициент значим.

Для коэффициента уравнения значимо отличного от нуля, строится доверительный интервал:

– находим по таблице Стьюдента уравнение значимости α и по числу степеней свободы n-k-1.

Согласно рисунку 2, интервальная оценка коэффициента уравнения с доверительной вероятностью будет иметь вид:

Таким образом, при увеличении Х5 на одну единицу У содержательно увеличится в среднем на 35,323.