3 Системы случайных величин

3.1 Понятие системы случайных величин

На практике результат опыта обычно описывается не одной, а двумя и более случайными величинами. Например, ошибки в определении координат летательного аппарата, ток помех в электронном усилителе имеет случайную амплитуду и фазу, входная и выходная величины любого прибора наблюдения также случайны и др.

Системой случайных величин называют множество двух и более случайных величин, рассматриваемых как единое целое при исследовании того или иного явления.

В зависимости от числа случайных величин, образующих систему, она называется двумерной, трехмерной, n-мерной. Будем обозначать их соответственно: (X,Y), (X,Y,Z),…, .

Геометрически их можно интерпретировать как векторы той или иной размерности. Систему двух случайных величин (X,Y) можно изобразить случайной точкой на плоскости с координатами X и Y или случайным вектором со случайными составляющими по осям X и Y (рис.3.1).

Рисунок 3.1 Интерпретация системы двух случайных величин (X,Y)

Аналогично систему трех случайных величин (X,Y,Z) можно изобразить случайной точкой с координатами X, Y и Z или случайным вектором в трехмерном пространстве (рис.3.2).

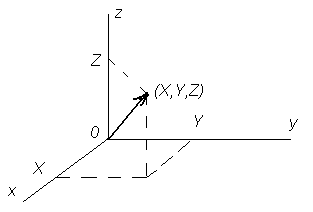
Рисунок3.2 Интерпретация системы трех случайных величин (X,Y,Z)

При изучении систем случайных величин стремятся найти:

а) координаты центра группирования системы случайных величин;

б) разброс случайных точек около центра группирования;

в) степень зависимости и вид связи случайных величин, входящих в систему.

3.2 Функция распределения системы двух случайных величин

Функцией распределения системы двух случайных величин (X, Y) называется функция двух аргументов F(X, Y), равная вероятности совместного выполнения двух неравенств: X<x, Y<y, где x и y – действительные числа:

.

Функция распределения системы двух случайных величин геометрически представляет собой вероятность попадания случайной точки (X, Y) в бесконечный квадрант с вершиной (x, y), расположенный левее и ниже этой вершины (рис. 3.3).

Рисунок 3.3 Геометрическая интерпретация функции распределения системы двух случайных величин

Геометрическая интерпретация функции распределения двумерной

случайной величины позволяет наглядно иллюстрировать ее свойства:

а) если один или оба аргумента стремятся к минусу бесконечности, то функция распределения стремится к нулю, т. е.

;

б) если один из аргументов стремится к плюсу бесконечности, то функция распределения системы стремится к функции распределения одной случайной величины, соответствующей другому аргументу, т.е.

;

в) если оба аргумента стремятся к плюсу бесконечности, то функция распределения системы стремится к единице

;

г) функция распределения является неубывающей функцией по каждому аргументу, т.е.

если , то ;

если , то .

Вероятность попадания случайной точки в заданную область.

Пусть имеется система случайных величин (X, Y), причем известна ее функция распределения F(X, Y). Требуется найти вероятность попадания случайной точки в заданную область R, т.е. .

Рисунок 3.4 Вероятность попадания случайной точки в заданную область R

Исходя из геометрической интерпретации, можно заметить (рис.3.4), что вероятность попадания случайной точки в заданную область R будет равна

.

Эта формула может использоваться как для случайных дискретных, так и непрерывных величин.