4.8.3. Теорема Кенига

Теорема: Кинетическая энергия СМТ в общем случае движения равна сумме кинетической энергии центра масс в предположении, что в нем сосредоточена вся масса СМТ, и кинетической энергии СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.

Доказательство.

Введем подвижную систему отсчета с началом в центре масс С, движущуюся поступательно относительно основной инерциальной системы отсчета. Представим скорость -й МТ, входящей в СМТ, относительно основной системы отсчета в виде (Ч.1 Кинематика):

, где – скорость движения центра масс СМТ, а – скорость -й точки СМТ по отношению к подвижной системе отсчета.

Подставив это выражение в соотношение (4.30), получим:

(4.42)

где – масса всей системы, – кинетическая энергия СМТ при ее движении относительно подвижной системы отсчета, перемещающейся вместе с центром масс поступательно.

На основании соотношений (4.6) и (4.16) для суммы во втором слагаемом правой части выражения (4.42) можно записать:

, так как .

Из соотношения (4.42) имеем теорему Кенига:

. (4.43)

4.8.4. Работа произвольной системы сил, приложенной к смт

Пусть к свободной СМТ приложена произвольная система сил . Выбрав в качестве полюса произвольную точку О СМТ, на основании теоремы о скорости точки СМТ в общем случае движения (Ч.1 Кинематика) скорость движения -й МТ относительно неподвижной системы координат выразится формулой:

, (4.44)

где – скорость полюса, – угловая скорость вращения СМТ вокруг мгновенной оси, проходящей через полюс О.

Для удобства сначала найдем мощность силы :

.

Второе слагаемое по свойству смешанного произведения и с учетом формулы для момента силы относительно точки (Ч.2 Статика) может быть записано в виде:

.

Подставляя это равенство в предыдущую формулу и используя определение скалярного произведения и связь между моментом силы относительно точки и оси (Ч.1 Статика), получим:

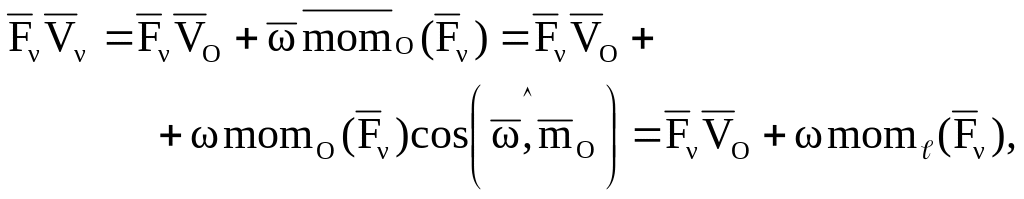
где – момент -й силы относительно мгновенной оси вращения , проходящей через полюс О.

Перейдем к определению элементарной работы силы .

Учтя соотношения , , , получим:

+ .

Тогда элементарная работа всех сил, действующих на СМТ, равна:

+

+ ,

где - сумма работ всех сил, действующих на СМТ, - главный вектор, а - проекция главного момента на ось  системы сил, действующих на СМТ.

Работа системы сил, действующих на СМТ, примет вид:

А= . (4.45)

В случае поступательного движения НМС соотношение (4.45) примет вид:

.

В случае вращательного движения НМС относительно неподвижной оси z соотношение (4.45) примет вид:

.

В случае, когда момент постоянен ( ), его работа выразится формулой:

.

4.9. Алгоритм решения задач с помощью теоремы

об изменении кинетической энергии СМТ – схема

алгоритма Д49 КЭС с комментариями и примерами

Комментарии

К.2. Рассматриваемый объект принимается за МC. Выделяются и нумеруются МТ и НМС, входящие в МC. На чертеже изображается силовая схема, т.е. рисуются все внешние силы и моменты, действующие на МC, в том числе внешние пассивные силы – силы реакций связей и реактивные моменты на основании принципа освобождаемости от связей (аксиома 5 статики). Если МС не является НМС, то в этом случае в силовую схему должны быть включены внутренние силы.

К.5,9. Все перемещения, необходимые для подсчета работы, и все скорости (линейные, угловые), необходимые для подсчета кинетической энергии, выражаются либо через те, которые заданы, либо через те, которые необходимо определить (в зависимости от числа степеней свободы МС).

Связь между перемещениями и между скоростями в зависимости от вида движений устанавливается с помощью соотношений, приведенных в Ч.1 Кинематика.

К.6. В случае, если МС является НМС, работа внутренних сил – Аⁱ будет равна нулю.

К.8а,9а. При подсчете кинетической энергии МТ, находящейся в сложном движении, необходимо помнить, что на основании теоремы о сложении скоростей в сложном движении (Ч.1 Кинематика).

К.8б,9б. Аналогичной формулой выражается кинетическая энер-гия МС, скорости всех точек которой равны (лента, трос, цепь).

К.9в,г. Моменты инерции определяются с помощью формул, приведенных в таблице 2.

К.9д. Первое соотношение представляет собой общую формулу кинетической энергии МС. Второе соотношение является теоремой Кенига (4.43), причем - это кинетическая энергия МС в ее относительном движении по отношению к поступательно движущейся системе координат с началом отсчета в центре масс.

К.10. Кинетическая энергия считается для начального и текущего или заданного моментов времени.

К.11. Для решения задач, связанных с ускорениями и мощностями, могут быть использованы две дифференциальные формы этой теоремы: , .

В этом случае мощности внешних – N^e и внутренних – Nⁱ сил определяются по формулам, аналогичным формулам, приведенным в процессе 5, только вместо перемещений записываются скорости (линейные, угловые).

Если МС является НМС, работы и мощности внутренних сил равны нулю и теорема об изменении кинетической энергии примет следующий вид (три формы):

, , .