4.8. Теорема об изменении кинетической энергии смт

4.8.1. Три формы теоремы

Используя теорему об изменении кинетической энергии МТ (соотношения (1.40), (1.42), (1.43)), для -й точки СМТ запишем:

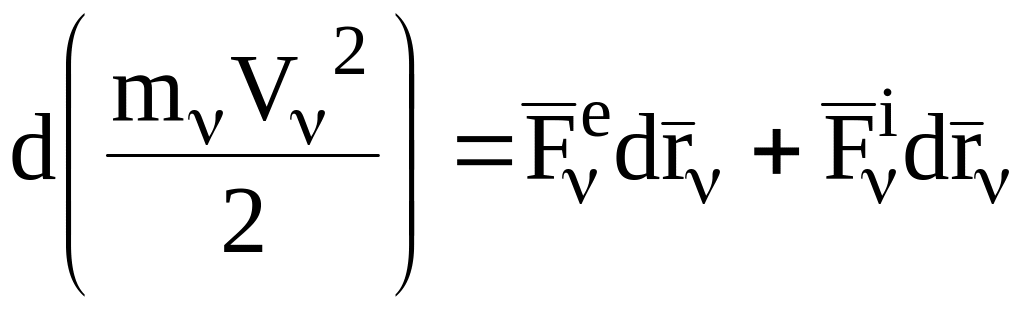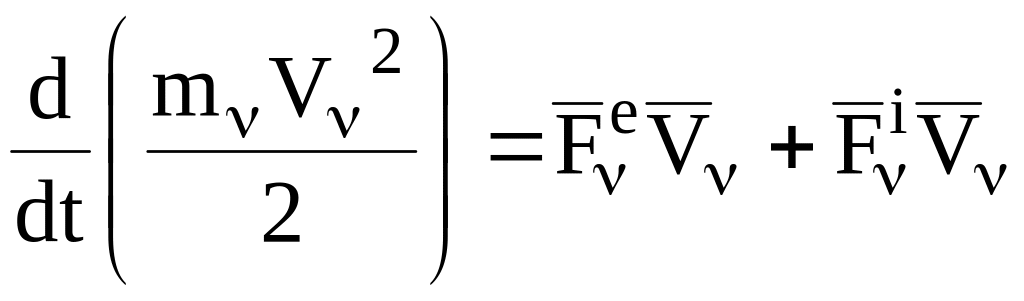(=1,…,n),

(=1,…,n),

(=1,…,n).

Просуммировав эти соотношения и учитывая, что производная от суммы равна сумме производных, получим:

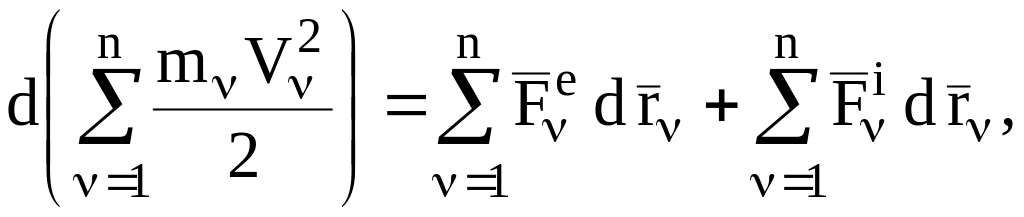
, (4.29)

.

Введем понятие кинетической энергии СМТ.

Определение: Кинетической энергией СМТ называется величина, равная сумме кинетических энергий входящих в нее МТ:

, (4.30)

аналогично

. (4.31)

Здесь Т и Т₀ – соответственно значения кинетической энергии СМТ в текущий и начальный моменты времени.

С учетом формулы (1.42) в соотношениях (4.29):

,

соответственно суммы элементарных работ всех внешних и внутренних сил, действующих на СМТ;

,

соответственно суммы их мощностей;

,

соответственно суммы работ всех внешних и внутренних сил, действующих на СМТ.

С учетом принятых обозначений, из соотношений (4.29) получим три формы (две дифференциальных и одну конечную) теоремы об изменении кинетической энергии СМТ.

Теорема: Дифференциал кинетической энергии СМТ равен сумме элементарных работ всех внешних и внутренних сил, действующих на СМТ.

. (4.32)

Теорема: Производная от кинетической энергии СМТ равна сумме мощностей всех внешних и внутренних сил, действующих на СМТ.

. (4.33)

Теорема: Изменение кинетической энергии СМТ на ее конечном перемещении из одного положения в другое равно сумме работ приложенных внешних и внутренних сил, на том же перемещении.

. (4.34)

Рассмотрим сумму элементарных работ всех внутренних сил, действующих на СМТ.

Выделим из СМТ две произвольные МТ В_ и B_, положение которых относительно неподвижного центра О определяется радиус-векторами . Обозначим через и ( ) силы взаимодействия между этими МТ и определим сумму элементарных работ этих сил (рис. 37):

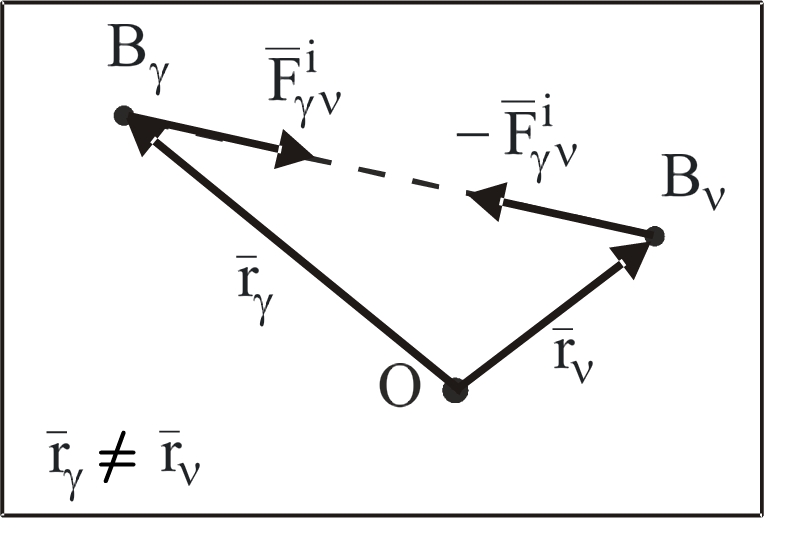
Рис. 37

Из полученного соотношения следует, что элементарная работа внутренних сил, с которыми две точки СМТ действуют друг на друга, будет равна нулю только в случае , т. е. когда , что имеет место в случае НМС.

Таким образом, сумма элементарных работ всех внутренних сил НМС всегда равна нулю. Аналогичным образом можно доказать, что суммы мощностей всех внутренних сил НМС и их работ будут равны нулю. Учитывая это, на основании соотношений (4.32) – (4.34) для НМС можно записать:

, (4.35)

, (4.36)

. (4.37)

4.8.2. Кинетическая энергия нмс в частных случаях движения

• Поступательное движение НМС.

В случае поступательного движения НМС все ее точки движутся с одинаковыми скоростями, равными скорости движения центра масс НМС: . Соотношение (4.30) в случае поступательного движения НМС примет вид:

. (4.38)

• Вращательное движение НМС вокруг неподвижной оси z.

В случае вращательного движения НМС все ее МТ движутся со скоростями , где - кратчайшее расстояние от -й МТ до оси вращения. Соотношение (4.30) в случае вращательного движения НМС вокруг неподвижной оси z примет вид:

. (4.39)

• Плоскопараллельное движение НМС.

В случае плоскопараллельного движения НМС в каждый момент времени движение НМС можно рассматривать как мгновенное вращательное движение относительно оси, перпендикулярной неподвижной (основной) плоскости и проходящей через мгновенный центр скоростей . Поэтому можно использовать соотношение (4.39)

, (4.40)

где – момент инерции НМС относительно мгновенной оси, перпендикулярной к неподвижной плоскости движения и проходящей через мгновенный центр скоростей.

Используем теорему Штейнера-Гюйгенса (3.22):

,

где J_С – момент инерции НМС относительно мгновенной оси, перпендикулярной к неподвижной плоскости движения и проходящей через центр масс С, а СР^v – расстояние между мгновенным центром скоростей и центром масс.

Подставив это выражение в соотношение (4.40), получим:

или

, (4.41)

где – скорость центра масс НМС.