Осевые моменты инерции однородных пластинок и стержней массы m

Форма пластинки	Jx	Jy	Jz
	0
Теорема Штейнера-Гюйгенса

В случае, если НМС имеет сложную конфигурацию, то момент инерции относительно какой-либо оси определяется по формуле: , где – радиус инерции, который определяется экспериментально.

Пример 1

2. Натяжение ведущей и ведомой ветвей ремня, приводящего в движение шкив радиуса , массы m, равномерно распределенной по ободу, соответственно N₁ и N₂ (N₁ > N₂). Чему должен быть равен момент сопротивления М_с для того, чтобы шкив вращался с угловым ускорением ?

МС состоит из одного АТТ – шкива.

Рис. 34

2. С04 ППВ

4 .

2. n = 1

3. Вращательное движение АТТ

6,7 , здесь , тогда

8. 1 – я задача динамики: определить М_с.

9. ( )

11 Ответ:

Пример 2

2. Однородный диск массы m₁, радиуса  вращается вокруг вертикальной оси z с постоянной угловой скоростью ₀. В точке D₀ находится МТ массы m₂ (рис. 35). В некоторый момент времени МТ начинает двигаться по внешней окружности диска с постоянной относительной скоростью u. Определить угловую скорость диска  в тот момент, когда МТ достигает положения D (DE || Оx). МС состоит из двух частей: диска – АТТ и МТ.

Решение задачи по алгоритму визуализировано.

Р ис. 35

2. С04 ППВ

4

2. n = 2.

Считается кинетический момент МС в момент времени, когда МТ находится в положении D.

 = 1

2. Вращательное движение АТТ.

3. По теореме Штейнера–Гюйгенса (формула (3.22))

Тогда

 = 2

5 МТ

6

Здесь .

Тогда

7. 

8. 2-я задача динамики,

9. 

10. 

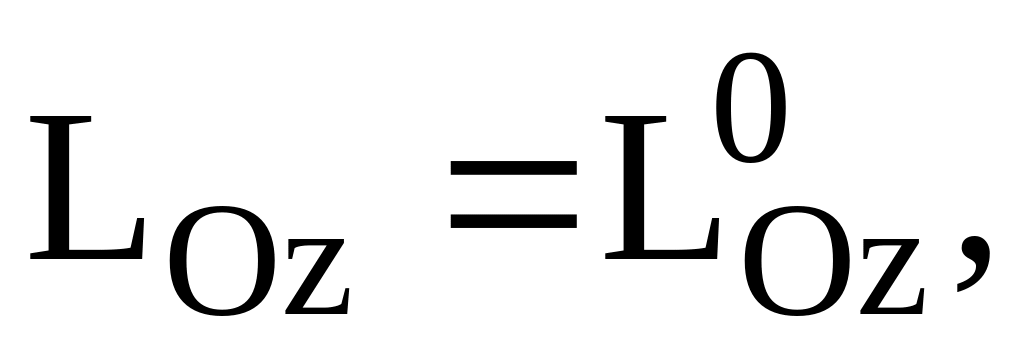
11. Ответ:

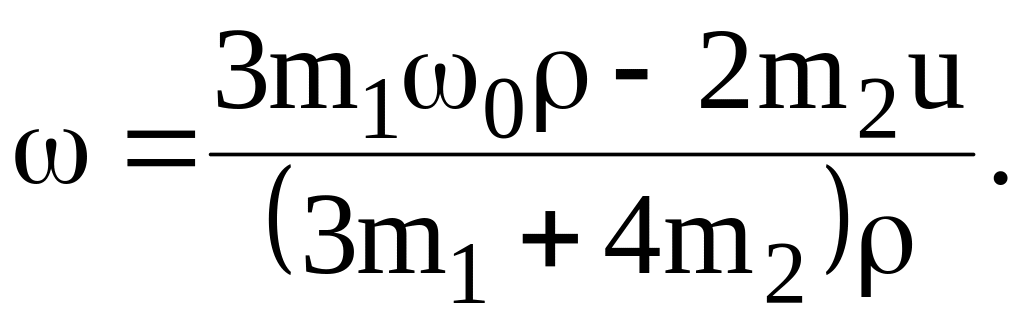
Пример 3

2. Два груза массы m₁ и m₂ подвешены на двух гибких нерастя жимых нитях, которые навернуты, как указано на рис. 36, на блок массы m₃ (радиусы ₁ и ₂ даны).

Рис. 36

Радиус инерции блока _u. Грузы движутся из состояния покоя под влиянием силы тяжести. Учитывая момент сопротивления вращению блока – определить угловую скорость блока как функцию времени и условие того, что груз массы m₁ будет опускаться. Массами нитей пренебречь. МС состоит из двух МТ и блока – АТТ.

2. С04 ППВ

4

Ось z проходит через точку С перпендикулярно плоскости блока.

2. n = 3.

 = 1

2. МТ 6 где  = 2

5 МТ 6 где

 = 3

5. Вращательное движение АТТ

6. здесь .

7. 

8. 2 – я задача динамики – определить  .  0.

9. 

10. Полученное уравнение интегрируется методом разделения переменных:

5. 

Очевидно, что груз массы m₁ будет опускаться при  > 0, т.е. > 0.