Ответы на экзаменационные вопросы по АиГ / 30

30.

Матричная запись и решение системы линейных уравнений. Вычисление обратной матрицы.

Матричная запись систем уравнений

 

Рассмотрим систему линейных уравнений с набором неизвестных:

Оперировать с такой системой, очевидно, не очень удобно. Эту же систему уравнений можно представить в более компактном матричном виде:

Ax=b

где b=(b₀,b₁,…,b_n)^T – вектор свободных членов и x=(x₀,x₁,…,x_n)^T – вектор неизвестных (вектор-решение) с вещественными координатами, а A=(a_ij)ⁿ_i,j=0 – вещественная NxN-матрица коэффициентов данной системы.

Матричный метод решения систем линейных уравнений.  

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.  Метод удобен для решения систем невысокого порядка.  Метод основан на применении свойств умножения матриц.   Пусть дана система уравнений:  Составим матрицы: A = 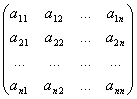; B = ; X = . Систему уравнений можно записать: AX = B. Сделаем следующее преобразование: A^-1AX = A^-1B, т.к. А^-1А = Е, то ЕХ = А^-1В Х = А^-1В  Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.  

Обращение квадратной матрицы

Поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку Inverse (Обратная матрица) на панели инструментов Matrix (Матрица). В листинге 7.16 приведен пример поиска обратной матрицы и последующая проверка правильности ее вычисления.

Листинг 7.16. Вычисление обратной матрицы