8. Параллельность прямой и плоскости. Параллельность плоскостей

Общий признак параллельности прямой и плоскости:

прямая параллельна плоскости, если она параллельна какой либо прямой этой плоскости.

Общий признак параллельности плоскостей:

если две пересекающиеся прямые одной плоскости па­раллельны двум пересекающимся прямым другой плос­кости, то эти плоскости параллельны между собой.

Применение этих признаков рассмотрим на примерах решения двух задач.

Задача 1. Через точку К провести плоскость, параллельную прямой m (рис.20)

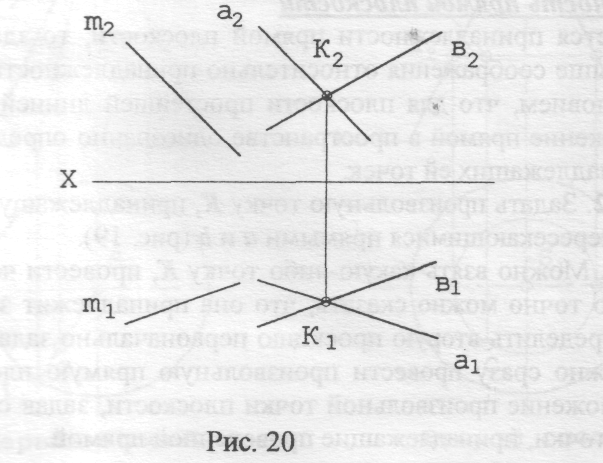
Краткую запись решения задачи 1 можно представить так.

Дано: m (m₁, m₂), К (К_1, К₂)

Провести: Σ // m ^ Σ К

Решение:

1. Σ(а b) => а Σ ^ b Σ => а₁ Σ₁ ^ b₁ Σ₁ =>а₂ Σ₂ ^ b₂ Σ₂

2. m // Σ => m // а Σ => а₁ // m₁ ^ а₂ // m₂

3. b - произвольно, решений - .

Задача 2. Через точку К провести плоскость Σ, параллельную плоскости Г(n m) (рис.21).

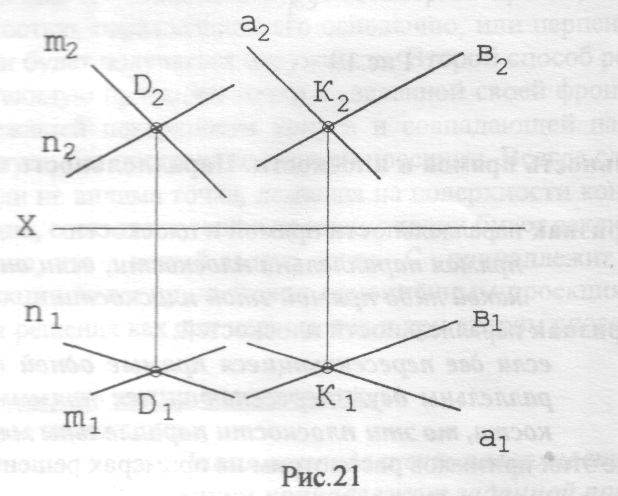
Краткая запись решения задачи 2 выглядит следующим образом.

Дано: Г (n m), m (m₁, m₂), n (n₁, n₂), К (К_1,К₂)

Провести: Σ // Г ^ Σ К.

Решение:

1. Σ(а b) => а Σ ^ b Σ => а₁ Σ₁ ^ b₁ Σ₁ =>а₂ Σ₂ ^ b₂ Σ₂

2. Σ // Г => а // m ^ b // n Σ => а₁ // m₁ ^ а₂ // m₂ ^ b₁ // n₁ ^ b₂ // n₂

Решение - единственное.

9. Главные позиционные задачи

Как в геометрической, так и в конструкторской практике большое число решений относится к задачам о пересечении геометрических образов или геометрических тел. Ввиду их особой важности, задачи о пересечениях называют главными позиционными задачами (ГПЗ).

Из всего разнообразия возможных при этом вариантов можно выделить две разновидности ГПЗ:

• 1ГПЗ: пересечение линий и поверхностей;

• 2ГПЗ: пересечение поверхностей.

Очевидно, что сказанное о двух ГПЗ характеризует самый общий вариант для каждой из задач и подразумевает, что понятие каждого из компонентов пересечения (линия, поверхность) включает в себя все возможные его варианты. Так, к 1 ГПЗ относятся пересечения:

• прямой линии и плоскости;

• прямой линии и поверхности; - кривой линии и плоскости;

• кривой линии и поверхности (в общем случае).

Ко 2-й ГПЗ относятся пересечения:

• плоскостей;

• плоскости и поверхности;

• поверхностей.

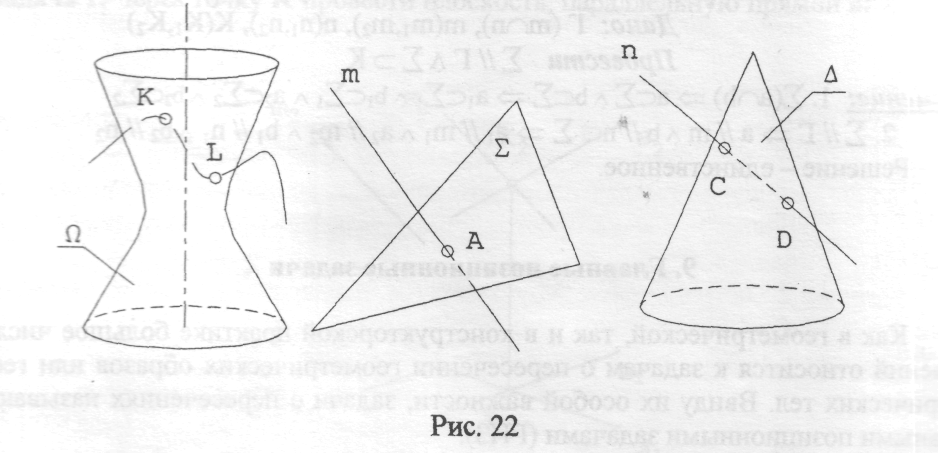
Сущность всякой задачи на пересечение состоит в определении общего элемента, который будем называть искомым геометрическим образом. Очевидно, в 1-й ГПЗ это - точка или несколько (конечное число) точек (рис.22). Во 2-й ГПЗ искомым геометрическим образом является линия (рис.23).

Искомый геометрический образ как результат пересечения заданных образов всегда принадлежит одновременно обоим заданным пересекающимся геометрическим образам и, очевидно, может быть определен:

• непосредственно, исходя из свойств пересекающихся образов;

• через посредство свойств нового геометрического образа или их совокупность.

Направление методики решения предполагает использование проецирующих свойств геометрических образов. Поскольку геометрические образы могут быть как проецирующие, так и не проецирующие, очевидно, что как для 1 ГПЗ, так и для 2 ГПЗ при всем многообразии вариантов возможно существо­вание трех случаев пересечения:

Случай 1. Оба пересекающихся геометрических образа проецирующего

характера;

Случай 2. Один из пересекающихся геометрических образов проецирующего характера, а второй — не проецирующий;

Случай 3. Оба пересекающихся геометрических образа - непроецирующего характера.

Имея в виду то определение главной проекции геометрического образа, которое было дано ранее, очевидно, можно утверждать, что

в случае 1 непосредственно на чертеже можно указать

обе проекции искомого геометрического образа;

в случае 2 непосредственно на чертеже можно определить

одну проекцию искомого геометрического образа;

В случае 3 определение проекций искомого геометрического образа потребует введения нового геометрического образа-посредника, обладающего свойствами проецирующих образов.

Эти соображения вытекают из того, что точка, линия, фигура, принадлежащая проецирующему геометрическому образу, будет иметь свои одноименные проекции, совпадающие с главной проекцией этого образа.

Все высказанное позволяет не только систематизировать все возможные случаи пересечения, но и алгоритмизировать сам процесс решения задач для все трех случаев.

Самое главное из всего вышеизложенного о главных позиционных задачах (ГПЗ) можно объединить в двух таблицах, полезных для использования при решении задач о пересечении геометрических образов.

Чтобы увидеть общее в решении задач на пересечение и выяснить алгоритм для того или иного случая пересечения, рассмотрим решения ряда задач.

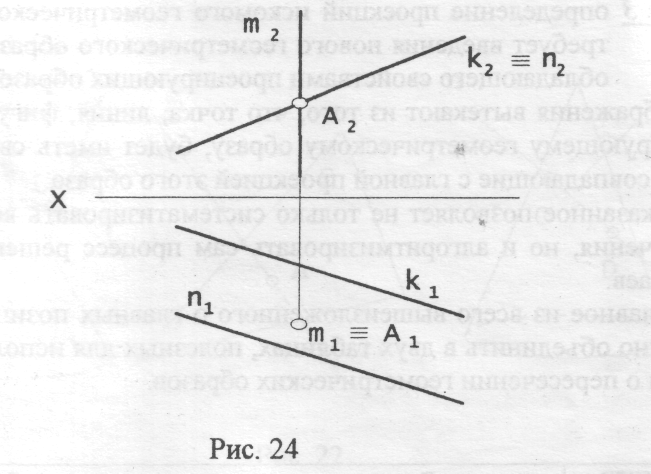
Задача 1 . Даны прямая m(m₁,m₂) и плоскость Σ(n//k).

Требуется определить точку А пересечения прямой m и плоскости Σ(n//k).

Решение (рис.24):

1. А m => А₂ m₂ А_] m_]

2. А Σ => А₂ Σ₂ (k₂ ≡ n₂) А₁ Σ₁(n₁//k₁).

1. m₁ ╨ П₁ => m₁ ≡ A₁

2. Σ ╨ П₂ =>Σ₂ А₂ А₂ = m₂ k₂ = n₂ (рис. 25)

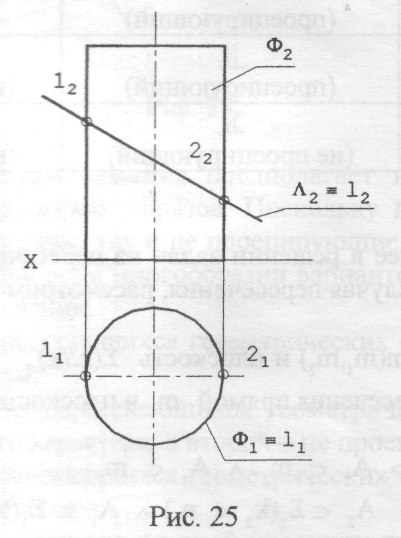
Задача 2 . Заданы плоскость ˄ (˄₂) и цилиндрическая поверхность Ф(Ф₁,Ф₂,) Определить линию пересечения l плоскости ˄ с поверхностью Ф.

Решение (рис. 25):

1.l ˄ => l₂ ˄₂ l_] ˄_]

2. l Ф => l₁ Ф₁ l₂ Ф₂

3. ˄ ╨ П₂ => l₂ ≡ ˄₂(l₂ 2₂)

4. Ф ╨ П₁ => Ф₁ ≡ l₁

Замечание. При рассмотрении интервала существования l необходимо помнить, что общность искомого геометрического образа определяет граница его существования в пределах общей принадлежности к заданным геометрическим образам (здесь эта граница определена точками 1 и 2).

Мы рассмотрели в задаче 1-1 ГПЗ, а в задаче 2-2 ГПЗ. Если сравнить их решения, можно заметить, что, во-первых, мы рассмотрели задачи, попадающие под первый случай пересечения, во-вторых, решение задач, в общем, не отличаются друг от друга. Значит, существует единый, общий для 1ГПЗ и для 2ГПЗ алгоритм решения, который мы сейчас и сформулируем.

Алгоритм решения для случая 1

1. Обе проекции искомого общего геометрического образа уже непосредственно заданы на чертеже.

2. Обе проекции искомого общего геометрического образа принадлежат главным проекциям проецирующих образов в пределах общ­ности этих проекций.

3. Решение задачи может быть сведено к простановке обозначений проекций искомого общего геометрического образа на чертеже.

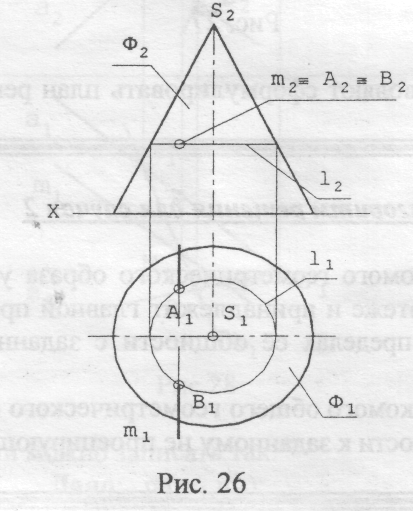
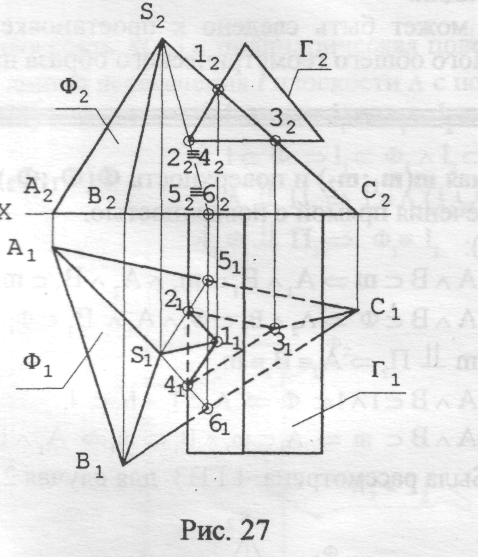
Примеры 3 и 4 позволяют сформулировать план решения задач для второго случая пересечения.

Алгоритм решения для случая 2

1. Одна проекция искомого геометрического образа уже непосредственно задана на чертеже и принадлежит главной проекции проеци­рующего образа в пределах её общности с заданным не проеци­рующим образом.

2. Другая проекция искомого общего геометрического образа определяется по принадлежности к заданному не проецирующему образу.

Задача 5 .Заданы прямая m общего положения и плоскость общего положения Σ в виде двух пересекающихся прямых а и в. Определить точ­ку М пересечения прямой m и плоскости Σ (рис. 28). Прежде, чем записать решение этой и следующей задачи, попробуем предложить следующий план решения.

Алгоритм решения 1ГПЗ для случая 3

1. Через заданную прямую проводится плоскость-посредник; целесообразно, чтобы эта плоскость была проецирующего характера.

2. Строится линия пересечения заданной плоскости и плоскости-посредника (второй случай пересечения!).

3. Определяется точка пересечения заданной прямой и построенной линии пересечения, которая и будет искомой точкой.

Эти же соображения можно сформулировать и в том случае, когда надо найти линию пересечения, а в качестве посредников выбраны некоторые поверхности. Сама же искомая линия будет представлена совокупностью точек.

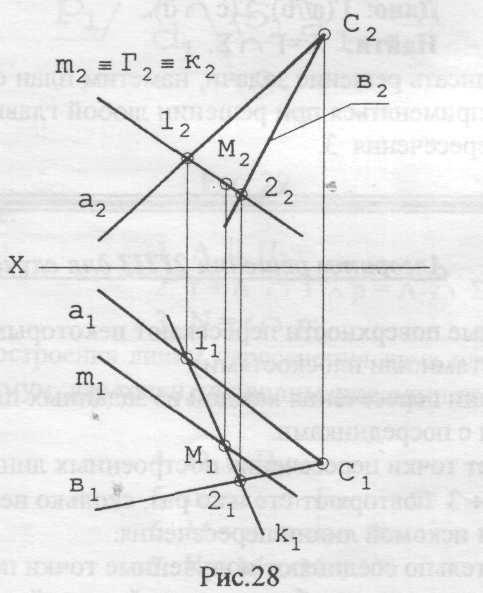
Данные этой задачи можно записать так:

Дано: m(m₁, m₂);

Σ(a b)= Σ₁(a₁ b₁) Σ₂(a₂ b₂)

Для задач на третий случай пересечения условимся записывать только решение в пространстве, что в более краткой форме отражает как суть производимых построений, так и применяемый алгоритм решения:

1. Г m ^ Г ╨ П₂;

2. k=Г Σ(а b);

3. М = m k.

Следует отметить, что посредник мог быть другим, однако в данном слу­чае проецирующее свойство посредника позволило использовать алгоритм для второго случая пересечения, что упростило задачу.

Рассмотрим еще один пример.

Задача 6. Даны две плоскости общего положения: плоскость Г задана параллельными прямыми а иb, плоскость Σ - пересекающимися прямыми с и d. Найти линию k пересе­чения этих плоскостей.

Кратко условие этой задачи можно записать так:

Дано: Г(а//b); Σ(c d). Найти: к=Г Σ.

Прежде чем записать решение задачи, наметим план её решения, который в дальнейшем будет применяться при решении любой главной позиционной задачи 2 для случая пересечения 3.

Алгоритм решения 2ГПЗ для случая 3

1. Обе заданные поверхности пересекают некоторыми посредниками (поверхностями или плоскостями).

2. Строят линии пересечения каждой из заданных плоскостей или поверхностей с посредниками.

3. Определяют точки пересечения построенных линий пересечения.

4. Пункты 1-3 повторяют столько раз, сколько необходимо точек для построения искомой линии пересечения.

5. Последовательно соединяют полученные точки пересечения в неко­торую линию, которая и будет искомой линией пересечения.

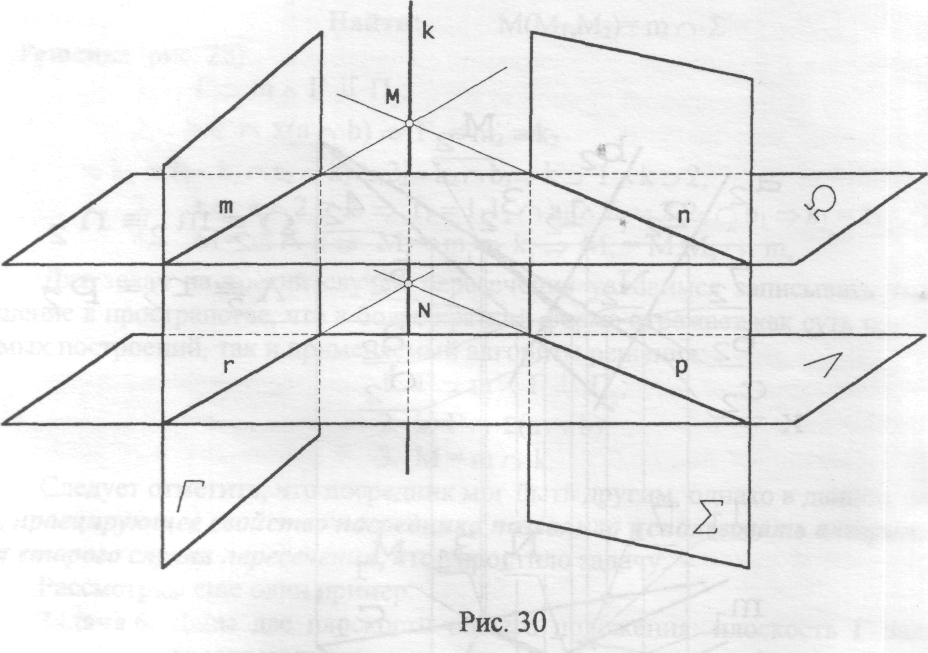
В этом варианте решение может быть записано так (рис. 29):

Решение:

1. ˄ ╨ П₂;

2. r = ˄ Г ^ p = ˄ Σ;

3. N = r p;

Так как для построения линии пересечения двух плоскостей - прямой - надо знать, как минимум, две точки, проводим еще один посредник (О.). Тогда:

4. Ω ╨ П₂;

5. m=Ω Г ^ n = Ω Σ;

6. М = m n;

7. К = M N.

То, что мы здесь проделали, можно проиллюстрировать рис. 30.

Заметим, что задача построения каждой из линий r, р, m и n - задача на второй случай пересечения, то есть, решение 2 ГПЗ для случая пересечения 3 к решению четырёх задач на второй случай пересечения!

Существует еще один способ определения линии пересечения двух поверхностей общего положения. Наиболее часто он используется в случае пере­сечения:

а) плоскостей;

б) плоскости и поверхности;

в) линейчатых поверхностей, из которых одна - гранная.

Тогда поступают следующим образом: