I. Основные понятия теории кривых
1. Плоская, пространственная, замкнутая, спрямляемая, гладкая, кусочно-гладкая кривая
Понятия
Множество
всех точек
,
координаты
и
которых определяются уравнениями
,
при
из
,
называется простой плоской кривой
,
если различным значениям параметра
из
отвечают разные точки из множества
.
Пространственная кривая -это кривая, точки которой не лежат в одной плоскости.
Замкнутая плоская кривая - это линия, которую можно изобразить на листе бумаги, не отрывая от него карандаша.
Если множество
ограничено сверху (снизу ограничено
нулем), то кривую
называют спрямляемой.
Кривую С будем называть гладкой
кривой, если среди ее параметрических
уравнений найдется такое, в котором
функции
и
непрерывно
дифференцируемы на отрезке, а их
производные отличны от нуля на этом
отрезке.
Кривая, представленная как сумма конечного числа гладких кривых, называется кусочно-гладкой.
2. Способы задания кривой, параметризуемая кривая
Понятия
Кривая называется
параметризуемой кривой, если
каждой ее точке поставлено в соответствие
определенное значение некоторого
параметра
,
пробегающего какой-то отрезок
.
3. Положительная и отрицательная ориентация кривой, противоположно ориентированная кривая
Понятия
Кривая с заданным направлением обхода
называется ориентированной кривой.
Для замкнутой кривой, лежащей в плоскости
,
положительным направлением обхода
называется такое направление, при
котором область, ограниченная этой
кривой, остается слева.
Если же она остается справа, то такое направление называется отрицательным направлением обхода.
4. Понятие длины дуги кривой, дифференциал дуги
Понятия
Длина дуги кривой — точная верхняя
граница S для множества
периметров
всевозможных вписанных в кривую ломаных
.
Пусть линия задана в
параметрическом виде,
где
непрерывно дифференцируемые на отрезке
функции.
При стремлении отрезка
ломаной к нулю можно считать, что
,
то есть является дифференциалом
дуги. Аналогично
,
соответствующие дифференциалы.
Тогда можно записать:
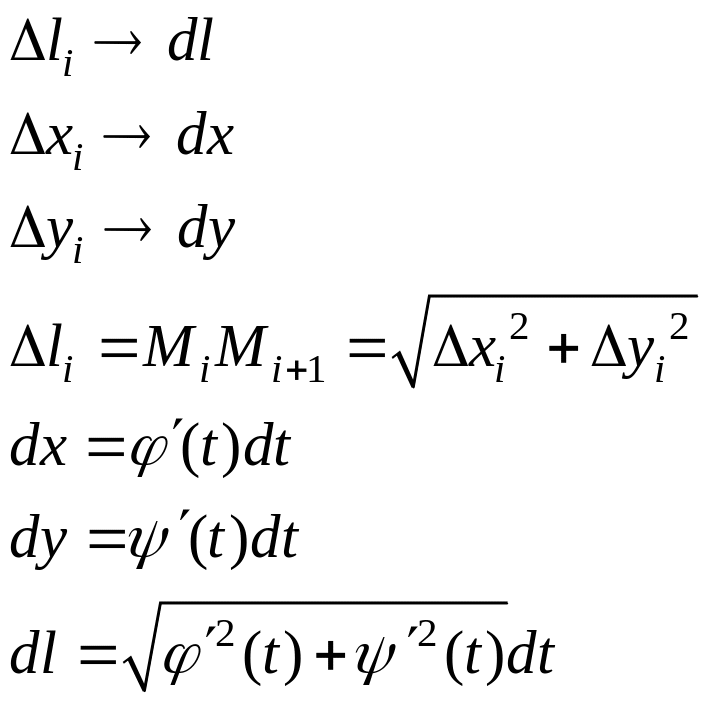
Эта формула для вычисления дифференциала дуги.
Умения
1.1. Нахождение дифференциала дуги
Найти дифференциал дуги кривой, если она задана в явном виде:
.
Решение:
Так как у нас кривая задана явно, то для нахождения дифференциала дуги кривой справедлива следующая формула:
.
В нашем случае получаем:
.
Ответ:
.
Найти дифференциал дуги
.
Решение:
Для нахождения дифференциала дуги заданной явно необходимо воспользоваться формулой:
.
Применим формулу для вычисления дифференциала нашей дуги:
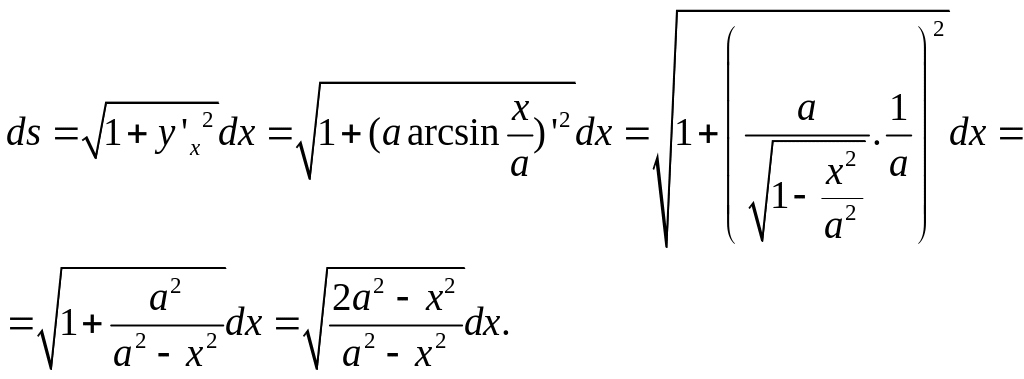
Ответ:
.
1.2. Нахождение дифференциала дуги
Найти дифференциал дуги кривой, если она задана в параметрическом виде:
Решение:
Воспользуемся следующей формулой:
.
И получим:
.
Ответ:
.
Найти дифференциал дуги
.
Решение:
Для нахождения дифференциала дуги заданной параметрически необходимо воспользоваться формулой:
.
Применим формулу для вычисления дифференциала нашей дуги:
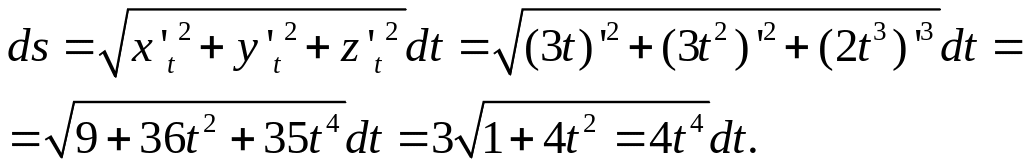
Ответ:
.
1.3.Нахождение дифференциала
Найти дифференциал дуги кривой, если она задана в полярных координатах:
Решение:
Используя формулу:
.
Подставим и в :
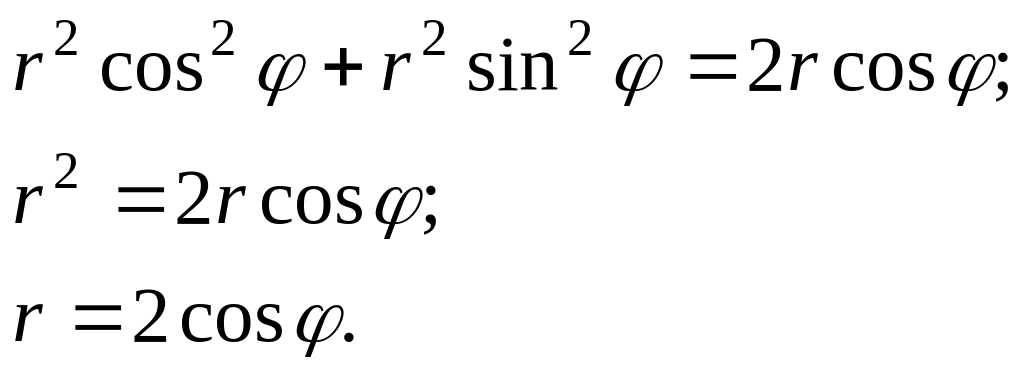
Воспользуемся вышеуказанной формулой:
.
Ответ:
.
Найти дифференциал дуги
.
Решение: Для нахождения дифференциала
дуги заданной полярно необходимо
воспользоваться формулой
.
Применим формулу для вычисления
дифференциала нашей дуги:
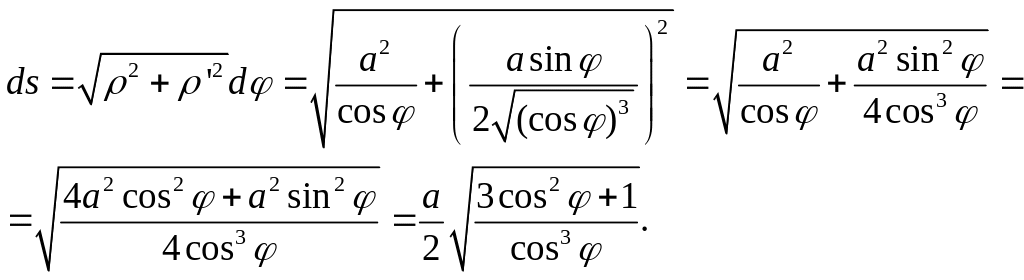
Ответ:
.
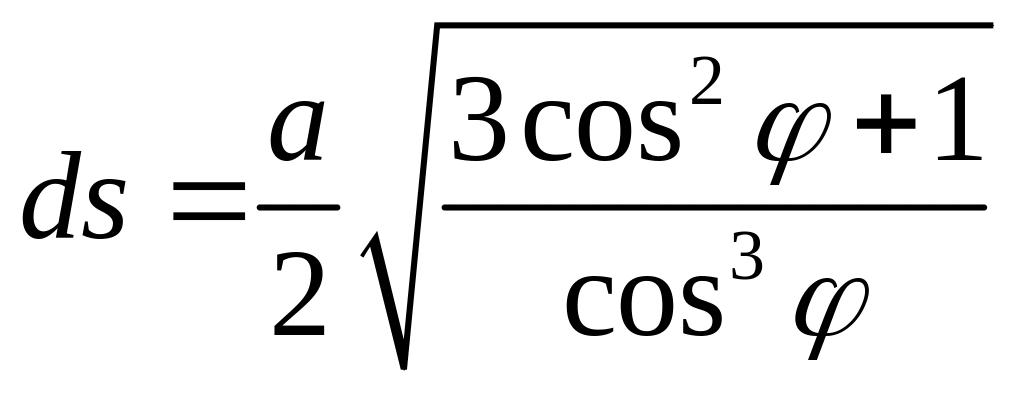