
3. Скалярное произведение векторов.
Под углом
между
ненулевыми
векторами
и
будем понимать угол между направленными
отрезками
и
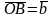 ,
имеющими общее начало и обозначается
,
имеющими общее начало и обозначается
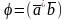 .
.
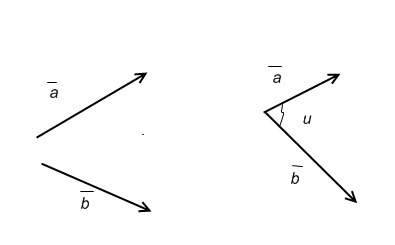
Векторы
и
называются ортогональными,
если угол между ними прямой
 =π/2
и обознается
.
=π/2
и обознается
.
Определение 15.
Скалярным
произведением
векторов
и
называется
число
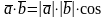
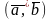 .
.
Если хотя бы один
из векторов
или
нулевой, то
неопределен
и считается
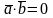 .
.
Пусть - вектор, l – прямая, точка ОÎ l. Отложим и построим точку A1 – ортогональную проекцию точки А на l.
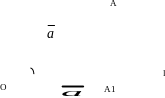
Говорят, что
ОА1
- проекция вектора
на ось l
и обозначают
ОА1
 .
.
Из прямоугольного
треугольника
ОАА1
получаем

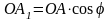
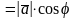 то есть
то есть

Теорема 7. (Свойства скалярного произведения векторов)
1.
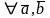 :
:
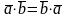
2.
:

3.
,
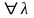 Î
ℝ:
Î
ℝ:

4.
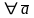 :
:

Доказательство.
1.
=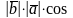
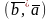 =
=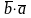
2. Учтем, что
=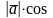
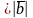 =
=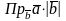 =
=
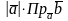 .
.
Тогда, применяя
свойства проекций получим
получим
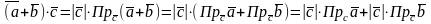 =
=
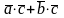 .
.
3.
Доказывается аналогично с учетом
свойства проекций:
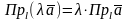
4. пппп
Теорема 8 (критерий
ортогональности векторов).
Пусть
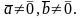 Тогда
Тогда
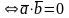
Доказательство.
а) Необходимость().
Пусть


=0.
а) Достаточность().
Пусть
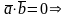
 =0.
Так как
=0.
Так как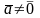 и
и
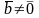 , то
, то
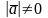 и
и
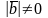
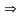 cos
=0
cos
=0
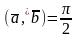 (поскольку
Î
[0,
π])
.
(поскольку
Î
[0,
π])
.
Определение 16. Базис { , , } пространства называется ортонормированным, если его различные векторы попарно ортогональны и их длины равны 1.
Векторы
ортонормированного базиса называются
ортами
координатных
осей
и обозначаются
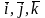 ,
то есть
,
то есть
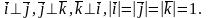
Определение 17. Аффинная система координат, базис которой ортонормирован, называется прямоугольной декартовой системой координат {О, }.
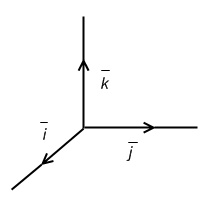
Для ортов справедливо
1) Скалярное
произведение одноименных ортов равно
1. Действительно,
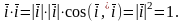 Аналогично
Аналогично
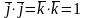 .
.
2) Скалярное
произведение разноименных ортов равно
0. Например,
 по теореме 8, так как
по теореме 8, так как
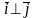 .
Аналогично
.
Аналогично

Теорема 9.
В ортонормированном базисе
скалярное произведение векторов
,
выражается через их координаты по
формуле
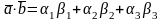 .
.
Доказательство следует из свойств скалярного произведения в ортонормированном базисе – Гл.
Следствие 9.1. Пусть в прямоугольной декартовой системе координат , . Тогда
1.
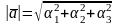
2. cos
=
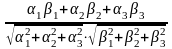
Доказательство.
1. По теореме 7,
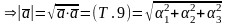
2.
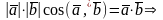
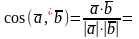 (теорема
9, сл. 9.1)
(теорема
9, сл. 9.1)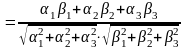
4. Векторное и смешанное произведение векторов.
Определение 18. Упорядоченная тройка некомпланарных векторов называется правоориентированной (правой), если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки, в противном случае тройка векторов называется левой.
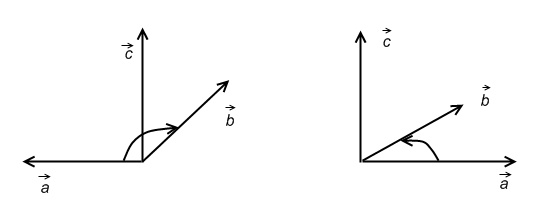
левая правая
Определение 19.
Векторным
произведением
вектором
и
называется
вектор
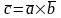 ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
1.
 ,
т.к.
,
т.к.
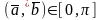
2.
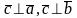
3. образуют правую тройку векторов
В частности, из п.1, определения 19 следует, что если хотя бы один из векторов равен , то их векторное произведение равно , поскольку имеет нулевую длину.
Теорема 10. (Свойства векторного произведения векторов)
1.
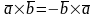 антикоммутативность.
антикоммутативность.
2. если
∦
,
то
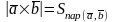 -
площадь параллелограмма, построенного
на векторах
и
.
-
площадь параллелограмма, построенного
на векторах
и
.
3.
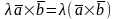
4.
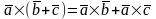
5. Пусть
Тогда
||
 .
.
Доказательство.
1.
Пусть
,
 ,
по определению 19,
,
по определению 19,
а)
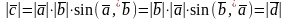 .
.
б)
 ;
;
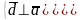
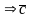 ||
||
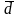 .
.
в)
- правая тройка,
 -
правая тройка
-
правая тройка
 ,
что видно из рисунка.
,
что видно из рисунка.

Из а-в), по определению
7 противоположного вектора, следует
 ,
что и требовалось доказать.
,
что и требовалось доказать.
2. Определение 19
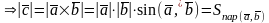
5. Необходимость
()
||
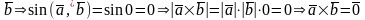 .
.
Достаточность ()
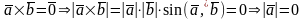 или
или
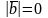 или
или
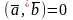
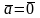 ||
или
||
или
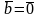 ||
или
||
.
||
или
||
.
Теорема 11. Пусть в правом ортонормированном базисе векторы заданы своими координатами , .
Тогда
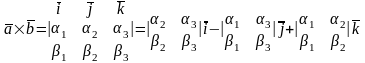
То есть
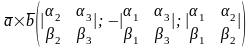 .
.
Из свойств векторного произведения следует, что
1) Векторное
произведение одноименных ортов равно
.
Действительно, по теореме 10 (5),
 ,
так как
,
так как
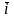 ||
,
||
,
 ||
,
||
,
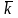 ||
.
||
.
2) Векторное произведение разноименных ортов находится по правилу
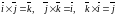
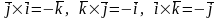 .
.
Определение 20.
Смешанным
произведением
векторов
называется число
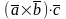 и обозначается
и обозначается
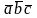 .
.
Теорема 12. (Свойства смешанного произведения векторов)
1. Смешанное
произведение векторов
по абсолютной величине равно объему
параллелепипеда, построенного на
:
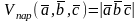 .
.
2.
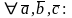
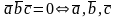 компланарны.
компланарны.
3.
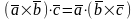 .
То есть, формально, в
записи смешанного произведения знаки
операций можно менять местами.
Исходя из этого в обозначении
не ставят знаки операций.
.
То есть, формально, в
записи смешанного произведения знаки
операций можно менять местами.
Исходя из этого в обозначении
не ставят знаки операций.
4.
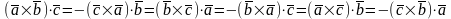 .
То есть, от
перемены мест двух любых сомножителей
в смешанном произведении знак смешанного
произведения меняется на противоположный.
.
То есть, от
перемены мест двух любых сомножителей
в смешанном произведении знак смешанного
произведения меняется на противоположный.
Теорема 13.
Пусть в правом ортогональном базисе
векторы заданы своими координатами:
,
,
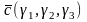 .
.
Тогда смешанное
произведение

Доказательство следует непосредственно из теорем 9 и 11.
