
2. Базис на плоскости и в пространстве. Координаты вектора и точки.
Теорема 3.
Пусть на плоскости даны два неколлинеарных
вектора
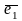 и
и
 .
Любой вектор
на
плоскости можно представить в виде
.
Любой вектор
на
плоскости можно представить в виде
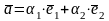 ,
где
,
где
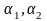 Î
ℝ,
причем
такое представление единственно.
Î
ℝ,
причем
такое представление единственно.
Доказательство.
I
. Существование.
Если
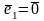 или
или
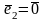 ,
то
||
,
что противоречит с условием, следовательно,
,
то
||
,
что противоречит с условием, следовательно,
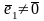 и
и
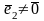 .
.
Если
||
,
то
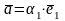 ,
для некоторого
,
для некоторого
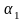 Î
ℝ
(см. опр.9)
и искомое разложение вектора
Î
ℝ
(см. опр.9)
и искомое разложение вектора
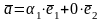 .
.
Если
||
аналогично существует
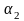 Î
ℝ:
Î
ℝ:
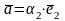 ,
т.е.
,
т.е.
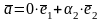 .
.
Если ∦ и ∦ , отложим , , от одной точки O. Пусть .
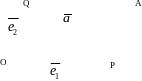
Проведем прямые
AP
и AQ,
такие что
||
AQ
и
||
AP
Тогда
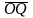 ||
,
следовательно,
=
||
,
следовательно,
=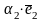 ,
,
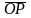 ||
,
следовательно,
=
||
,
следовательно,
=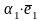 для некоторых
Î
ℝ.
для некоторых
Î
ℝ.
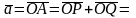
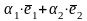 -
искомое разложение.
-
искомое разложение.
II.
Единственность.
Пусть
 ,
где, например,
,
где, например,
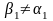 ,
тогда, вычитая почленно, получим
,
тогда, вычитая почленно, получим
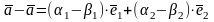 ,
где
,
где
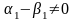 .
Далее,
.
Далее,
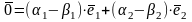 ,
,
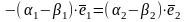 | :
| :
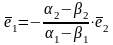 ,
откуда следует по опр.9, что
||
,
противоречие условию. Теорема доказана.
,
откуда следует по опр.9, что
||
,
противоречие условию. Теорема доказана.
Аналогично доказывается
Теорема 4.
Пусть даны три некомпланарных вектора
,
,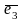 .
Любой вектор
в
пространстве может быть представлен в
виде
.
Любой вектор
в
пространстве может быть представлен в
виде
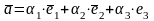 ,
где
,
где
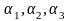 Î
ℝ,
причем
такое представление единственно.
Î
ℝ,
причем
такое представление единственно.
Определение 11. Базисом на плоскости назовем два неколлинеарных вектора на плоскости, взятых в определенном порядке.
Базисом в пространстве назовем три некомпланарных вектора, взятых в определенном порядке.
Определение 12.
Если
,
,
-
базис в пространстве и
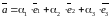 ,
то числа
называются координатами
вектора
относительно
данного
базиса
и обозначается
(
).
,
то числа
называются координатами
вектора
относительно
данного
базиса
и обозначается
(
).
Аналогично определяются координаты вектора на плоскости. В дальнейшем все понятия, вводимые для пространства можно перенести на случай плоскости.
Пусть т.О фиксированная точка пространства, , , - базис в пространстве.
Определение 13. Аффинной системой координат в пространстве называется совокупность т.О – начала координат и базиса , , в пространстве и обозначается {O, , , }.
Пусть М
– произвольная точка пространства.
Радиус-вектором
точки
М
по отношению к началу координат
О называется
вектор
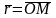 .
.
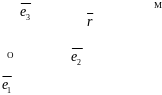
Определение 14. Координаты радиус-вектора точки М по отношению к началу координат называются координатами точки М в рассматриваемой системе координат.
Иначе говоря, точка
М
имеет координаты x,
y,
z
в системе координат
{O,
,
,
},
если
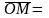
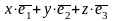 и записывается M(x,y,z).
и записывается M(x,y,z).
Лемма 1.
Координаты вектора
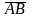 в
системе координат {O,
,
,
}
равны разности координат его начальной
и конечной точки.
в
системе координат {O,
,
,
}
равны разности координат его начальной
и конечной точки.
Т.е. если
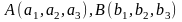 ,
то
,
то
 .
.
Доказательство.
A
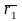
B
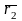
O
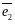
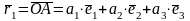
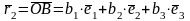
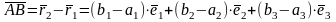 ,
т.е.
,
т.е.
.
Теорема 5.
Пусть в аффинной системе координат {O,
,
,
}
векторы заданы своими координатами
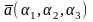 ,
,
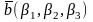 ,
тогда умножение вектора на скаляр и
сложение векторов производится
покоординатно, т.е.
,
тогда умножение вектора на скаляр и
сложение векторов производится
покоординатно, т.е.
1.

2.
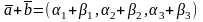
Доказательство.
1. Так как
 ,
то
,
то
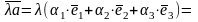 (т.2)
(т.2)
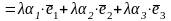 ,
т.е.
,
т.е.
2. Так как
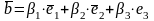 ,
то
,
то
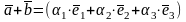 +
+
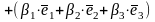 =(т.1,
т.2)=
=(т.1,
т.2)=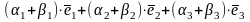 ,
то есть
,
то есть
Теорема 6.
Пусть в аффинной системе координат {O,
,
,
}
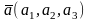 ,
,
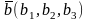 ,
,
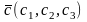 .
.
Векторы
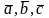 компланарны
компланарны
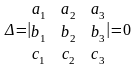
Доказательство.
а) Необходимость (). Пусть компланарны.
Если хотя бы один
из векторов равен
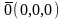 ,
то очевидно ∆=0.
,
то очевидно ∆=0.
Если какие-либо
два вектора коллинеарны, например
||
,
то
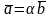 ,
то есть
,
то есть
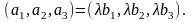 По свойствам определителей, вынося
за знак определителя, получим
По свойствам определителей, вынося
за знак определителя, получим

Пусть
∦
∦
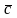 .
Разложим
по
векторам
и
,
как по базису на плоскости (см. теорему
3): существуют
Î
ℝ:
.
Разложим
по
векторам
и
,
как по базису на плоскости (см. теорему
3): существуют
Î
ℝ:
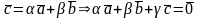 .
В координатной форме:
.
В координатной форме:
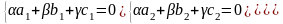 (*) ;
(*) ;
 (**)
(**)
Т.е., согласно (**), третья строка в ∆ может быть получена как линейная комбинация первых двух. По свойствам определителей ∆=0.
б) Достаточность
().
Пусть ∆=0. Решая систему (*) относительно
неизвестных α,
β и γ,
получим, что ее основная матрица А
вырождена, так как ее определитель имеет
вид ∆=0 и, следовательно, rangA<3.
Значит, (*) имеет бесконечное множество
решений среди которых есть хотя бы одно
ненулевое, то есть решение (α,β,γ)(0,0,0).
Таким образом, существуют α,β,γ
не равные нулю одновременно, удовлетворяющие
(*), следовательно,
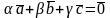 .
Пусть, например,
.
Пусть, например,
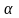
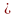 0.
Тогда
0.
Тогда
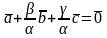 ;
;
 .
.
То есть разлагается по и , как по базису на плоскости, значит, принадлежит плоскости, проходящей через и . Теорема доказана.
