7. Основные свойства двойного интеграла
Свойства двойного интеграла (и их вывод) аналогичны соответствующим свойствам однократного определенного интеграла.
1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D1 и D2, то функция f(x, y) интегрируема в каждой из областей D1 и D2, причем
2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D, причем
3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.
4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то
5°. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем
(Конечно, из интегрируемости |f(x, y)| в D не вытекает интегрируемость f(x, y) в D.)
6°. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула
(11)
В частности, если функция f(x, y) непрерывна в D, а область D связна, то в этой области найдется такая точка (ξ, η), что μ = f(ξ, η), и формула (11) принимает вид
7°. Важное
геометрическое свойство. 
равен
площади области D (Это
свойство, как уже отмечалось ранее,
непосредственно вытекает из определения
интегрируемости, данного в пункте Определение
и существование двойного интеграла для
произвольной области)
_________________________________________________________________
8. Двукратный интеграл и его свойства
9. Связь двойного и двукратного интеграла
Пусть в ограниченной замкнутой области
D плоскости Оху
задана непрерывная функция z=f(x,y)
(не обязательно положительная). Разобьём
область D на n
частей D1, D2,
… Dn
с площадями
и диаметрами d1,
d2, … dn.
Выберем внутри каждой области Di
произвольную точку Mi(xi,yi)
и составим сумму:
. (1)
Сумма (1) называется n-й
интегральной суммой функции f(x,y),
соответствующей данному разбиению
области D и данному
выбору точек Мi.
Пусть
.
Конечный предел, если он существует, n-й интегральной суммы (1), когда наибольший из диаметров частичных областей стремиться к нулю, называется двойным интегралом от функции f(x,y) по области D .
Обозначается:
,
(2)
D – область интегрирования.
Различают два основных вида области интегрирования.
1. Область интегрирования D
ограничена слева и справа прямыми x=a
и x=b
(a<b),
а снизу и сверху – непрерывными кривыми
и
,
,
каждая из которых пересекается
вертикальной прямой только в одной
точке
(рис 12.). Такая область называется правильной по х.
Для такой области интеграл вычисляется по формуле
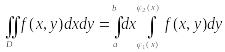(3)
причем сначала вычисляется внутренний интеграл
,
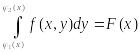в котором x считается постоянным. Далее, полученную функцию от x интегрируем по промежутку от a до b.
2. Область интегрирования D
– ограничена снизу и сверху прямыми y
= c и y
= d (c<d),
а слева и справа - непрерывными кривыми
,
каждая из которых пересекается
горизонтальной прямой только в одной
точке (рис 13.). Такая область называется
правильной по у.
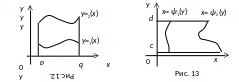В
этом случае двойной интеграл вычисляется
по формуле
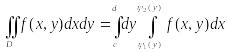(4)
причем сначала вычисляется внутренний интеграл, в котором у считается постоянным.
Правые части формул (3) и (4) называются двукратными интегралами.
Если область интегрирования правильная, двойной интеграл не зависит от порядка интегрирования.
Замечание 1. Двойной интеграл – число, поэтому пределы во внешнем интеграле всегда постоянны.
Замечание 2. Если область интегрирования – прямоугольник, со сторонами, параллельными осям координат, то пределы интегрирования постоянны как во внешнем, так и во внутреннем интеграле:
Замечание
3. Формула (3) получена для
,
исходя из геометрического смысла
двойного интеграла. Оказывается, что
она справедлива для любой непрерывной
функции в области
.
_________________________________________________________________
10. Двойной интеграл в полярных координатах
Рассмотрим двойной интеграл
(1)
Пусть требуется вычислить интеграл (1) в полярной системе координат, причем полюс совпадает с началом координат
и полярная ось совпадает с осью абсцисс. Декартовы координаты точки выражаются через полярные по формулам:
(2)
Элемент
площади в полярной системе
(3)
Чтобы преобразовать интеграл (1) к
полярной системе координат, нужно х
и у в функции f(x,y)
выразить через
и
по формулам (2) и взять элемент площади
(3):
(4)
Для вычисления двойного интеграла в полярной системе координат его сводят к повторному.
и
и кривыми
и
,
причём линии
пересекают границу не более чем в двух
точках
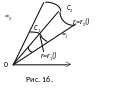
(С1 и С2). Тогда
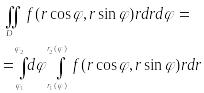
б) Полюс
и любой луч
пересекает границу области только в
одной точке . Тогда
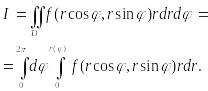
Замечание. Двукратные интегралы
могут иметь постоянные пределы лишь в
том случае, когда границей области D
служат координатные линии
и
.
_____________________________________________________________________
Если мы составим
интегральную сумму для функции
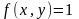по области D,
то эта сумма будет равна площади S,
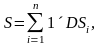
при любом способе разбиения. Переходя к пределу в правой части равенства, получим
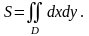
Если область D правильная , то площадь выразится двукратным ингралом
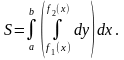
Производя интегрирование в скобках, имеем, очевидно,
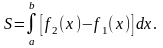
Пример 2. Вычислить
площадь области, ограниченной кривыми
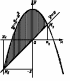
Рис.19
Решение. Определим
точки пересечения данных кривых (Рис.19).
В точке пересечения ординаты равны,
т.е.
,
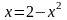отсюда
Мы
получили две точки пересечения
Следовательно, искомая площадь
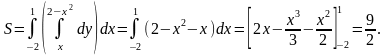
5. Вычисление площади поверхности
Пусть требуется
вычислить площадь поверхности,
ограниченной линией Г (рис.20); поверхность
задана уравнением
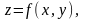где функция
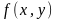непрерывна и имеет непрерывные частные
производные. Обозначим проекцию линии
Г на плоскость Oxy
через L.
Область на плоскости Oxy,
ограниченную линией L,
обозначим D.
Разобьём произвольным
образом область D
на n
элементарных площадок
В
каждой площадке
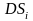возьмём точку
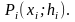Точке Pi
будет соответствовать на поверхности
точка
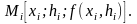Через точку Mi
проведём касательную плоскость к
поверхности. Уравнение её примет вид
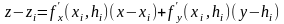(1)
На этой плоскости
выделим такую площадку
,
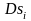которая проектируется на плоскость Оху
в виде площадки
.
Рассмотрим сумму всех площадок
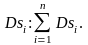
Предел
этой суммы, когда наибольший из диаметров
площадок
-
стремится к нулю, мы будем называть
площадью
поверхности,
т. е. по определению положим
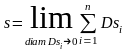(2)
Займемся теперь
вычислением площади поверхности.
Обозначим через
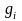угол между
касательной плоскостью и плоскостью
Оху.
Рис.20 Рис.21
На основании известной формулы аналитической геометрии можно написать (рис.21)
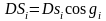
или
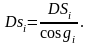(3)
Угол есть в то же время угол между осью Oz и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеем
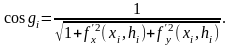Следовательно,
Подставляя это выражение в формулу (2), получим
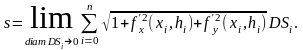
Так как предел
интегральной суммы, стоящей в правой
части последнего равенства, по определению
представляет собой двойной интеграл
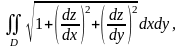то окончательно получаем
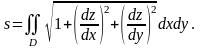(4)
Это и есть формула,
по которой вычисляется площадь поверхности
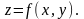
Если уравнение
поверхности дано в виде
или в виде
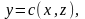то соответствующие формулы для вычисления
поверхности имеют вид
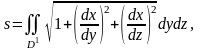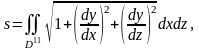(3’)
(3’’)
где D’ и D’’ - области на плоскостях Oyz и Oxz, в которые проектируется данная поверхность.
________________________________________________________
12. Тройной интеграл и его свойства