
Элементы векторной алгебры
1. Вектор. Операции над векторами
Под направленным отрезком будем понимать отрезок AB, для которого указано его начало – т.А и конец – т.B.
Два направленных отрезка называются коллинеарными, если они расположены на одной прямой или на параллельных прямых и обозначаются AB // CD.
Направленные отрезки AB и CD называются одинаково направленными, если они коллинеарны и концы их B и C лежат в одной полуплоскости относительно прямой, проходящей через их начала A и B и обозначаются AB ↑↑ CD. (рис 1)
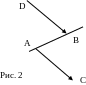

Направленные отрезки AB и CD называются противоположно направленными, если они коллинеарны и их концы C и D лежат в разных полуплоскостях относительно прямой AB и обозначаются AB ↑↓ CD. (рис. 2)
Определение 1. Два направленных отрезка называются эквивалентными, если они одинаково направлены и длины их равны.
Эквивалентность направленных отрезков обладает свойствами рефлексивности, симметричности и транзитивности. Отсюда, по основной теореме об отношении эквивалентности, множество всех направленных отрезков разбивается этим отношением на пересекающиеся классы эквивалентности.
Определение 2.
Вектором называется класс эквивалентных
отрезков и обозначается
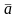
Пусть
-
вектор, и направленный отрезок AB
его представитель, т.е. AB
принадлежит классу
.
Тогда будем обозначать
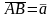 ,
т.е. вектор
представлен
направленным отрезком AB.
,
т.е. вектор
представлен
направленным отрезком AB.
В качестве
представителя вектора
может
быть выбран любой вектор CDÎ
,
т.е.
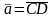 .
Тогда справедливо
.
Тогда справедливо
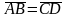 .
.
Пусть A – произвольная точка и - вектор, тогда существует т.B, такая что ABÎ , т.е. .
Операция построения
направленного отрезка AB,
т. что
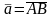 называется откладыванием
вектора
от
т.А. (рис. 3)
называется откладыванием
вектора
от
т.А. (рис. 3)

Определение 3.
Векторы
и
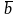 называются
коллинеарными
и обозначаются
||
называются
коллинеарными
и обозначаются
||
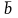 ,
если они могут быть представлены
направленными отрезками, лежащими на
параллельных прямых.
,
если они могут быть представлены
направленными отрезками, лежащими на
параллельных прямых.
Определение 4. Векторы называются компланарными, если они могут быть представлены направленными отрезками, параллельными одной плоскости.
Определение 5.
Длиной
вектора
называется длина
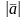 любого
из направленных отрезков, образующих
.
любого
из направленных отрезков, образующих
.
Определение 6.
Нулевым
вектором
называется вектор
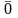 ,
представленный нулевым направленным
отрезком, начало и конец которого
совпадают.
,
представленный нулевым направленным
отрезком, начало и конец которого
совпадают.
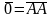 .
.
Замечание. Для любого вектора считается || .
Определение 7.
Вектором, противоположным вектору
называется
вектор
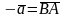 .
.
Операции над векторами
Определение 8.
Пусть
и
-
векторы,
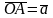 и
и
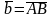 .
Суммой
векторов
и
называется
вектор
.
Суммой
векторов
и
называется
вектор
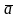 +
,
представленный отрезком OB,
т.е.
+
,
представленный отрезком OB,
т.е.
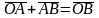 при последовательном откладывании
векторов
и
.
при последовательном откладывании
векторов
и
.
Правило сложения векторов по определению 8 называется
правилом треугольника для сложения векторов (рис.4):
1. Отложить векторы последовательно, т.е. начало второго совпадает с концом первого.
2. Построить вектор с началом в начале первого вектора и концом в конце второго.
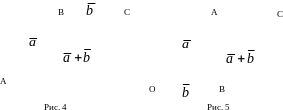
Из рис.5 очевидно, что вектор + может быть также представлен диагональю параллелограмма, построенного на векторах и , отложенных от одной точки. Отсюда вытекает
правило параллелограмма для сложения векторов:
1. Отложить векторы от одной точки О.
2. Построить на векторах параллелограмм.
3. Построить вектор, равный диагонали параллелограмма, с началом в т.О.
Теорема 1. Множество всех векторов в пространстве образует абелеву группу относительно операции сложения векторов.
Доказательство. Множество всех векторов замкнуто относительно операции сложения, так как сумма векторов по определению 8 является вектором.
Ассоциативность:
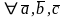
Пусть
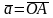 ,
,
,
,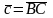 .
По определению 8,
.
По определению 8,
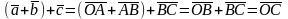
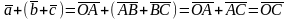 ,
ассоциативность доказана.
,
ассоциативность доказана.
2. Существует нейтральный элемент (см. опр.6), такой что
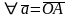
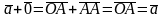
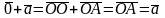
3.
существует противоположный вектор (см.
опр.7)
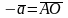 ,
,
такой что
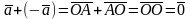
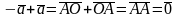
4. Коммутативность операции сложения
,
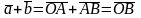 (1) см рис. 6.
(1) см рис. 6.
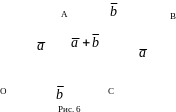
Отложим теперь
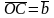 .
Тогда OABC
– параллелограмм. Отсюда
.
Тогда OABC
– параллелограмм. Отсюда
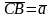 .
.
Тогда
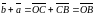 (2). Из (1) и (2) следует
(2). Из (1) и (2) следует
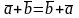 .
Теорема доказана.
.
Теорема доказана.
Определение 9.
Произведением
числа
λÎ
ℝ
на
вектор
называется
вектор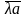 ,который
удовлетворяет условиям:
,который
удовлетворяет условиям:
1.
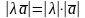
2. ↑↑ при λ>0
↑↓ при λ<0
Замечание:
при λ=0 |
|=0,
следовательно,
=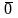 .
.
Теорема 2. Для умножения числа на вектор справедливы свойства:
1.
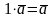 (унитарность);
(унитарность);
2.
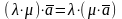 (обобщенный ассоциативный закон);
(обобщенный ассоциативный закон);
3.
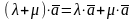 (обобщенный дистрибутивный закон);
(обобщенный дистрибутивный закон);
4.
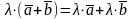 (обобщенный дистрибутивный закон).
(обобщенный дистрибутивный закон).
Из теоремы 1 и теоремы 2 следует, что множество всех векторов в смысле опр.2 является векторным пространством относительно операции сложения и умножения на число по опр.8 и опр.9.
Утверждение.
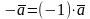
Доказательство.
По опр.7, если
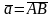 ,
то
,
т.е.
,
то
,
т.е.
 .
Кроме того,
.
Кроме того,
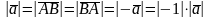 .
По опр.9 получаем
.
По опр.9 получаем
Определение 10.
Разностью векторов
и
называется
вектор
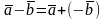
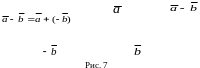
Из определения 10 и рис.7 следует
правило
нахождения разности
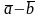 :
:
1. Отложить и от одной точки.
2. Соединить концы и .
3. Выбрать направление от конца вычитаемого к концу уменьшаемого .
